Time

Time is a physical quantity. The generally used formula symbol of time is t, its SI unit is the second s.

Time describes the sequence of events, thus has a definite, non-reversible direction. Using the physical principles of thermodynamics, this direction can be determined as an increase in entropy, i.e. disorder in a closed system. From a philosophical perspective, time describes the progression of the present coming from the past and leading towards the future. According to the theory of relativity, time forms with space a four-dimensional space-time, in which time takes the role of a dimension. Thereby, the concept of the present is definable only in a single point, while other points of space-time, which are neither in the past nor in the future of this point, are called "spacelike separated" from this point.

In the SI system of units, time is one of several basic quantities.

The time is used to indicate a point in time. As civil time (UT, CET, etc.), it is approximately based on the position of the sun and is uniform within a time zone due to government regulations.

In philosophy, one has always asked about the nature of time, which also touches on topics of worldview. For the physical, biological and human sciences, time is a central parameter that can also be measured, for example in all moving bodies (dynamics, development), in chronobiology or the sociology of time. Psychology examines the perception of time and the sense of time. Economics also considers time as an object of value. In linguistics, "time" means the grammatical form of time words, the tense.

Introduction

Probably the most striking property of time is the fact that there always seems to be a place, in some sense current and excellent, which we call the present, and which seems to move inexorably from the past towards the future. This phenomenon is also called the flow of time. This flowing, however, defies consideration by the natural sciences, as will be argued below. Even the humanities cannot clarify the question unambiguously.

In physics, time serves to describe events in a manner analogous to that of space. Physics states that among all conceivable structures in three-dimensional space in combination with all conceivable temporal processes, only those are observed which obey the laws of physics. These can just as well be regarded in a four-dimensional space, the space-time, as immobile structures, which are subjected to certain geometrical conditions by the physical laws. According to Newton, the structure of this space-time is thereby predetermined, with time having absolute significance; according to Albert Einstein, a special "relativity of simultaneity" applies. Something that could be interpreted as the flow of time occurs in physics only through probabilistic terms related to the concept of entropy (see below), although the concepts of past, present and future in Einstein's theories are mathematically precise and have measurable meaning. On closer examination, however, it initially turns out to be completely unclear how a flow of time could be precisely described in the language of physics or mathematics or any other science.

For example, the statement that time flows is only meaningful if an alternative that can be distinguished from it is conceivable. The obvious alternative of the notion of a stagnant time, for example, however, leads to a contradiction, since it is only conceivable from the point of view of a second observer, for whom time continues to pass, so that the assumed standstill as such is perceptible at all (see also Immanuel Kant's Critique of Pure Reason: "If one could stop time, for how long would time 'stand'?").

The apparent flow of time is therefore considered by many physicists and philosophers to be a subjective phenomenon or even an illusion. It is thought to be very closely related to the phenomenon of consciousness, which likewise defies physical description or even explanation and is thus one of the great mysteries of natural science and philosophy. Thus our experience of time would be comparable to the qualia in the philosophy of consciousness and would consequently have as little to do with reality primarily as the phenomenal content of consciousness in the perception of the color blue with the corresponding wavelength of light.

This would invalidate our intuitive idea that there is an instance independent of our own person, like a cosmic clock, which determines which point in time we are all experiencing together at the moment, and which thus makes the present an objective now that unites us all.

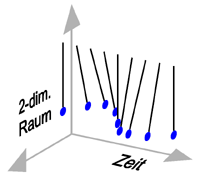
Swinging phases of a pendulum at different times. In this representation of events, there is no flow of time.

Time as a physical quantity

In physics, time (formula symbol: t or τ, from Latin tempus (time)) is the fundamental quantity by which, together with space, the duration of processes and the sequence of events can be determined. Since it cannot yet be traced back to more fundamental phenomena, it is defined by methods for its measurement, as is the case with space and mass. In the SI system of units, time is measured in seconds (unit symbol s). The units minute and hour are derived directly from this, and indirectly (via the earth's movement and legally defined leap seconds) also day and week, plus (depending on the calendar) month, year, decade, century and millennium.

Timing

The measurement of time is one of the oldest tasks of astronomy. After it was demonstrated in the first half of the 20th century that the length of the mean solar day is subject to irregular variations and increases in the long term, ephemeris time was introduced, based on the more regular planetary motion. Its unit of time, the ephemeris second, was adopted as the International System of Units second in 1960. Since 1967/68, the definition of the SI second has been based on the period of a particular oscillation in the ^{133Cs atom,} while maintaining as closely as possible the original length of the second. The most important time scales today are

• the International Atomic Time TAI, whose unit is the SI second on the geoid.
• Universal Time UT1, which depends on the current angle of rotation of the Earth, i.e. it is a form of mean solar time. It is irregular and can be measured with an accuracy of a few microseconds.
• the Coordinated Universal Time UTC, which follows the second cycle of the TAI, but only deviates from UT1 by a maximum of 0.9 s due to the occasional insertion of leap seconds. It or a zone time dependent on it is the civil time.
• the Terrestrial Time TT, which replaced the Ephemeris Time in astronomy in 1984, in order to be able to correctly handle the relativistic time dilation due to motion and gravitation. It agrees very exactly with TAI + 32.184 s on the geoid. In addition, there is the related Barycentric Dynamic Time TDB, which differs from TT on the geoid by a maximum of 2 ms, as well as the two coordinate times TCG and TCB; see Dynamic Time.

Astronomical dates and times are often conveniently given as Julian dates (JD) or modified as Modified Julian dates (MJD).

Today, time in physics, like other measurands, is defined operationally, i.e. via a measurement procedure. For the measurement of time, systems are mainly used which, according to the general view, periodically (i.e. after equal time intervals) return to the same state. Time is then determined by counting the periods. Such a device is called a clock. However, monotonous movements can also be the basis of time measurement, e.g. in the earlier sand and water clocks.

A watch is better the more accurately the periodic process can be reproduced and the less it can be influenced by external conditions, such as mechanical disturbances due to fluctuations in temperature or air pressure. Therefore, quartz clocks are much more accurate than mechanical clocks. The most accurate clocks are atomic clocks, which are ­based on atomic oscillation processes. ­This means that a relative rate error of 10-15 is achievable, which corresponds to a deviation of one second in 30 million years. Time and thus also frequency, its mathematical reciprocal, are the physical quantities that can be measured with the highest precision of all. This has led, among other things, to the definition of length now being reduced to that of time, by defining the metre as the distance travelled by light in a vacuum during 1/299,792,458 of a second.

Newtonian physics

Isaac Newton describes the phenomenon of time in the following words:

The fundamental concept of "absolute time" was long considered "self-evidently true" in physics, from about 1700 until 1905, i.e. until the formulation of the special theory of relativity by Albert Einstein. The Newtonian concept of time still underlies the everyday understanding of the phenomenon, although many precision measurements have proven that not Newton but rather Einstein was "right".

Quantum Mechanics

Although the energy-time uncertainty relation Δ at first sight has the form of Heisenberg's uncertainty relation, it is of a different nature. In quantum mechanics, time is not an observable (like location, energy, etc.) but a parameter. There cannot be an operator for a corresponding measurand, because attempts to introduce it run into contradictions.

Theory of Relativity

Due to discoveries in connection with electromagnetic waves, the Newtonian concept of an absolute time which is the same at every place in the universe had to be abandoned. In particular, the independence of the speed of light from the speed of the moving light source or the moving receiver cannot be explained in any other way than that two observers judge temporal processes differently when they move relative to each other (see special relativity). This applies both to the simultaneity of events occurring at different locations and to the duration of time between two meetings of two observers moving relative to each other between these meetings (time dilation). Since there is no absolutely stationary coordinate system, the question of which observer correctly judges the situation is not meaningful. Therefore, one assigns to each observer its so-called proper time. Furthermore, the presence of masses affects the passage of time, so that it passes at different speeds at different locations in the gravitational field. Thus Newton's assumption that time passes without reference to external objects is no longer tenable.

Time and space appear in the basic equations of relativity almost completely equivalent next to each other and can therefore be united to a four-dimensional space-time. Mathematically, however, one is not dealing with a four-dimensional Euclidean space, the , but with a Minkowski space . In this space, not and have analogous metric structure, but, for example, and , where the speed of light and is the "imaginary unit" of the complex numbers. So space and time are not completely identical even in special relativity. This leaves the possibility of the special temporal behavior in thermodynamic processes (see below).

In three-dimensional space, the choice of the three coordinate axes is arbitrary, so that concepts such as left and right, up and down, front and back are relative. In special relativity, it turns out that the time axis is not absolute either. Thus, as the state of motion of an observer changes, so does the orientation of its time and space axes in spacetime. This is a kind of shear motion of these axes, which is mathematically closely related to rotations. Thus, space and time can no longer be clearly separated, but depend on each other in a non-trivial way (so-called Lorentz transformations). The consequences are phenomena such as relativity of simultaneity, time dilation and length contraction. These properties of time and space, which were discovered in connection with the theory of relativity, are largely beyond our comprehension. However, they can be precisely described mathematically and are also well confirmed experimentally. However, the time axis cannot be reversed by a movement, i.e. past and future cannot be interchanged; the resulting theory retains the fundamental property of causality.

Time is not necessarily unlimited in general relativity. Thus, many physicists assume that the Big Bang is not only the beginning of the existence of matter, but also the beginning of space and time. According to Stephen W. Hawking, a point in time "one second before the Big Bang" did not exist any more than a point on the Earth that lies 1 km north of the North Pole.

In 2008, however, Martin Bojowald developed a theoretical model within the framework of loop quantum gravity (SQG) in which the universe existed even before the Big Bang. The usual cosmological models of general relativity have their limitations here due to a singularity contained in the SQG model.

Time Travel

The relativistic effects mentioned can in principle be interpreted as time travel. The extent to which travel into the past is also possible in principle via the curvature of space-time and other phenomena has not been conclusively clarified. Possible candidates are so-called wormholes, which could connect regions of space-time with different times, furthermore special trajectories in the vicinity of a sufficiently fast rotating black hole and finally the vicinity of two cosmic strings, which fly past each other sufficiently fast. However, the effort required to make practical use of any of these potential possibilities would far exceed the current resources of mankind.

The paradoxes that occur when travelling into the past could be avoided within the framework of Everett's many-worlds theory. According to this theory, the past to which one travels would be located in a parallel world. The original course of events and the one modified by the time travel would both take place in parallel and independently of each other.

Time and causality

The concept of time is closely ­related to the concept of causality. ­Thus we take it for granted that the cause occurs before its effect or simultaneously with it; more precisely, any observer of correlated events ­will describe the process in such a way that in his model of the process the effect is caused by the cause. The past is immutable; it cannot be affected by present events. The future, on the other hand, depends causally on the present, so it can be influenced by events or actions in the present.

In relativity, the temporal order of events occurring at different spatially separated locations is judged differently by observers moving relative to each other. This is precisely the case if the two events could only come into contact through a signal with faster-than-light speed. If such an interaction could take place with faster-than-light speed, then one could send a message into the past with the following system:

1. The signal is sent at faster-than-light speed to a relay station sufficiently far away.
2. This conventionally accelerates away from the original transmitter (alternatively: it conventionally transmits the signal to another relay station moving away from the receiver, e.g. the other side of a rotating platform). This "shifts" the sending event from the past into the future.
3. Finally, the signal is sent back again at faster-than-light speed. If the velocities involved are sufficiently high, the signal arrives before the original signal is sent out.

Therefore the principle of causality would be violated. In the middle of the 20th century, conjectures were made as to whether faster-than-light tachyons could exist. Should they be able to interact with ordinary matter, causality would be violated. The conjecture of the existence of tachyons therefore has few supporters.

On the symmetry of the two directions of time

The laws of physics, which underlie electromagnetism and gravitation and thus the phenomena of our everyday life, are invariant with respect to an inversion of time. This means that for every process that obeys these laws, the time-reversed one is also possible in principle. This statement contradicts our everyday experience. If a ceramic cup falls to the ground, it breaks into shards. It has never been observed, however, that these shards reassemble themselves into an intact cup. However, such a process would not in principle contradict the laws of nature. It is merely extremely unlikely.

The background of this circumstance is a probability consideration, ­which is formulated ­in the second law of thermodynamics. According to this, in a closed system of many particles, the entropy, which indicates the degree of disorder, can practically only increase and thus its order decrease. The opposite, a spontaneous increase in order, is not excluded in principle, but is all the less probable the greater the increase and the greater the number of particles involved. In order to be able to experience, for example, the spontaneous reunion of shards to form a cup, one would have to create and observe a more than astronomical number of piles of shards.

The second law of thermodynamics - and also the friction phenomena connected with it - thus violate the symmetry concerning the two directions of time. Therefore, the theorem cannot be derived from the basic laws of physics, but has the property of a postulate. The two directions of time thus lose their equivalence, and one speaks of the thermodynamic arrow of time. It is regarded as a potential basis for the flow of time from the past into the future, as we experience it in our everyday world.

In this context, there is often talk of the reversibility or irreversibility of time. However, this is a linguistic and logical inaccuracy. If someone could reverse time, then he would only see all processes running backwards if his own subjective perception of time were excluded from the reversal. The reversed course of time would thus only be discernible from the point of view of an observer who is subject to a kind of personal time that continues to run forward unchanged. However, such a splitting of time into two - one that is reversed in the thought experiment, and a second unchanged - makes no sense.

The laws of physics describing the phenomena of the weak and strong interaction are not invariant with respect to a time reversal. To a process in the field of nuclear and elementary particle physics, the time-reversed is therefore not necessarily compatible with the laws of physics. It would be, if it was not only time-reversed, but additionally considered as a mirror image and proceeded with antimatter instead of matter. This is the content of the CPT theorem, which is one of the best confirmed laws of physics. From the CPT-theorem follows that processes, which show a violation of the CP-symmetry, as they occur with some elementary particles, cannot be invariant with respect to a time reversal.

In the formalism of the description of antimatter, antiparticles are equivalent to ordinary particles moving backwards in time in some sense. In this sense, the pair annihilation of a particle with its antiparticle has a formal resemblance to a single particle that begins to move backwards in time at this point, so that it exists there twice and does not exist at all in the future.

Limits of the physical concept of time

There is clear evidence that the phenomenon of time loses its properties as a continuum in the range of the Planck time of 10-43 s. Thus, the consistent application of the known laws of physics leads to the result that any process shorter than Planck time can only be assigned to an object that must immediately collapse into a black hole (see Planck Units). This consideration shows that the known laws of physics fail beyond Planck time. It is hoped that the questions involved will be clarified by a yet-to-be-developed theory of quantum gravity, which would unify the two fundamental theories of physics, relativity and quantum physics. In such a theory, time would possibly be quantized in the range of Planck time. For example, in loop quantum gravity, a candidate theory of quantum gravity, the structure of spacetime is thought to be a four-dimensional, foam-like spin network with "bubbles" of the order of Planck units. However, one must not imagine this "foam" embedded in space and time, but the foam is space and time in this theory.

Atomic Clock


Astronomical clock in Prague Old Town