Tide

This article deals with tides specifically on Earth. The causes of tides on all celestial bodies are in the article Tidal Forces.

Tide is a redirect to this article. For other meanings, see Tide (disambiguation).

The tides (Low German Tid, Tied [tiːt] "time"; pl. Tiden, Tieden [tiːdən] "times") are the movements of water in the oceans caused by the associated tidal forces as a result of the gravitational pull of the moon and the sun. The tides predominantly affect the coasts. Since the stronger influence comes from the moon, there are not two high tides and two low tides in 24 hours, but in just under 25 hours, because the moon is only in approximately the same position in the sky again after an average of 24 hours 49 minutes.

The tidal forces act in the sense of a symmetrical stretching of the earth along the line to the moon or the sun. Since no stable deformation can occur due to the Earth's rotation, the tidal forces periodically stimulate currents in the oceans, especially in the middle latitudes. These cause the water level to rise and fall periodically. At full and new moon, the sun and moon are on the same line from the earth, which is why their effects add up to a particularly large tide, the spring tide. At half moon, on the other hand, the sun and moon are at right angles to each other, resulting in a particularly small tide, the neap tide. The tidal forces of the sun are about 46% of those of the moon.

Particularly large tidal forces and spring tides occur about every 15 months, when the moon is again very close to the earth due to the slow rotation of the elliptical lunar orbit. In addition, the variable inclination of the moon's orbit to the earth's axis results in an approximately annual variation of the tides.

The science of the earth's maritime tides is called tidology. Its basic statements are part of nautical training.

High and low tide at a jetty in the Bay of Fundy

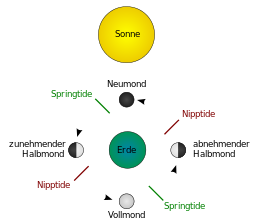
Schematic representation of the occurrence of Spring and Nipple Tides; inertias cause Spring Tides, for example, to occur somewhat later than at full and at new moon.

Sandbanks in the tidal area of the Lower Saxony Wadden Sea National Park (2019)

Explanation of the tides

Tides are caused by the interaction of the Earth's daily rotation in the (almost fixed) gravitational field of the Moon and the Sun, and the fact that this gravitational field is not equally strong everywhere, but pulls the Earth slightly along. The forces that cause this are called tidal forces. A location on the Earth's surface reaches a point of maximum tidal force and a point of minimum tidal force twice in each revolution. Although the tidal force accounts for less than one ten-millionth of the Earth's gravitational pull, it is a periodic disturbance of an otherwise stable state of equilibrium. The oceans respond to this disturbance with back-and-forth oscillating currents, which become noticeable on coasts by periodic raising and lowering of sea level. In many places, differences in height of well over 1 metre are reached.

Explanation of tidal forces

A gravitational field invokes an acceleration ) at an otherwise force-free mass point (mass at location ${\vec {r}}$ due to the gravitational force ${\ddot {\vec {r}}}={\vec {a}}({\vec {r}})$ rise to ${\vec {F}}({\vec {r}})=m\;{\vec {a}}({\vec {r}})$ an acceleration Considering an extended cloud of mass points that feel no gravitational forces other than these, the center of mass of the cloud at its location ${\vec {R}}$ will ${\ddot {\vec {R}}}$ exhibit a certain acceleration as if the sum of gravitational forces of all mass points here acted on a body with the sum of their masses (see the center-of-mass theorem).

One relates the gravitational acceleration of the center of mass at location ${\vec {r}}$ to the acceleration of the center of mass. The difference is the tidal acceleration prevailing at that location of the cloud:

${\vec {a}}_{\text{Gez}}({\vec {r}})={\vec {a}}({\vec {r}})-{\ddot {\vec {R}}}$

The tidal acceleration shows itself directly in the acceleration of the motion of the (otherwise force-free) mass point relative to the center of mass of the cloud. In the reference frame in which the center of mass is at rest, each mass point behaves as if the tidal force

${\vec {F}}_{\text{Gez}}({\vec {r}})=m\;{\vec {a}}_{\text{Gez}}({\vec {r}})$

acts. Alternatively to this derivation, one can explicitly perform a transformation of the reference frame from an inertial frame to the rest frame of the center of mass of the cloud. This reference frame is ${\ddot {\vec {R}}}$ accelerated with hence an inertial force ${\vec {F}}_{\text{Träg}}({\vec {r}})=-m\;{\ddot {\vec {R}}}$ , which one has to add to the external force . ${\vec {F}}({\vec {r}})=m\;{\vec {a}}({\vec {r}})$ The result for the tidal force - which is the force effective in this reference frame - is the same.

The same tidal force also works, if the mass points, of which the celestial body under consideration consists, feel further forces, e.g. mutual gravitation, cohesion etc., but also a further external force field. However, in the accelerated movement of a mass point, the tidal force does not appear directly, but only in the sum with the other forces acting on the mass point. It then can cause e.g. deformations and/or flows, depending on how fix mass-points are bound to their location.

This derivation of tide-acceleration and tide-force is valid independent of track or motion-state of celestial body (e.g. linear or circled, with or without rotation). The assumptions made in many textbooks, for example, about its circular motions and the associated centrifugal forces (which, by the way, are only exact for uniform circular motion) serve there merely to determine the acceleration of the center of mass in order ${\ddot {\vec {R}}}$ to be able to perform the transformation into its system of rest.

The tidal force caused by a celestial body is strongest at the two opposite points of the earth's surface, which have the smallest and largest distance to the celestial body. There it points vertically outwards, i.e. at the smallest distance directly towards the celestial body, at the greatest distance directly away from it. At points on the earth's surface which are the same distance from the celestial body as the earth's centre of mass, the tidal force is smallest and points vertically inwards. At an intermediate range, the tidal force is directed parallel to the Earth's surface and can therefore efficiently drive currents in the ocean.

Why does the sun's gravitational field pull the earth a bit?

For a simple explanation, instead of the solid earth, consider a fictitious spherical cloud of small particles that orbit the sun together, but do not exert any forces on each other (not even gravity). All particles move (at first) with the same angular velocity ω $\omega$ around the sun, partly a little closer, partly a little further away from it. Then, at the location of the cloud's center of gravity, the total gravitational force exerted by the sun on the particles yields exactly the centripetal acceleration ω $\omega ^{2}\,R$ necessary to continue its circular motion (with radius ) (see center-of-mass theorem). Compared to the center of mass, particles closer to the Sun need a smaller centripetal acceleration for their orbit at the same angular velocity, but feel a stronger gravitational pull from the Sun. Therefore, their orbit becomes more curved toward the Sun and they move away from the center of the cloud at an increasingly faster rate. Conversely, particles at a greater distance than feel a smaller gravitational pull from the Sun and cannot be held in a circular orbit by it. So these particles will accelerate outward away from the center. Result: the cloud is pulled apart along the line to the sun in both directions. This "tidal breakup" has already been observed with comets that come too close to a planet (see Shoemaker-Levy 9). Now the Earth is not a cloud of non-interacting particles, but the tidal forces are the same. As a solid body with some elasticity, the Earth deforms, and does so (by the Sun and Moon combined) by ±30 to ±60 cm (see Earth Tides), while currents are generated in the moving air and water masses of the atmosphere and oceans.

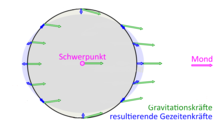
Tidal acceleration (blue) due to the Moon for locations on the Earth's surface as the difference between the local gravitational acceleration (green) and the acceleration of the center of mass.

Calculation of tidal accelerations

Tidal accelerations are acceleration differences between different points of an external field. The external field is always a superposition of central fields, here mainly of sun and moon. The simplest case is that of a central field, i.e. of the sun or moon. The accelerations are determined using a test mass, which is placed once at the location of the center of mass of the Earth and once at the location of interest. The acceleration at the center of mass is equal to the acceleration of a rigid earth. The other location of the test mass can be anywhere in the earth, e.g. in the moving hydrosphere.

$a(r)={\frac {GM}{r^{2}}}$

is the amount of acceleration in the gravitational field of the other celestial body (sun or moon) given by Newton's law of gravity. Where is the distance of the test mass from the causative mass and is the gravitational constant. For points on the line connecting the center of mass of the Earth to the celestial body, the accelerations are parallel, so the maximum and minimum tidal accelerations are simply calculated by the difference of the magnitudes at the points and $R\pm r_{0}$ ( $r_{0}$ for the mean radius of the Earth):

$a_{\text{Gez}}(\pm r_{0})=a(R\pm r_{0})-a(R)\ \approx \ -{\frac {2GM}{R^{3}}}\;\cdot (\pm r_{0})$ .

With $r_{0}=6{,}371\cdot 10^{6}\,{\text{m}}$ and the values for the Moon, $GM=4{,}90\cdot 10^{12}\,{\text{m}}^{3}/{\text{s}}^{2}$ and $R=3{,}84\cdot 10^{8}\,{\text{m}}$ , results in.

$a_{\text{Gez}}(+r_{0})=-1{,}07\,10^{-6}{\text{m/s}}^{2}$ and

$a_{\text{Gez}}(-r_{0})=+1{,}13\,10^{-6}{\text{m/s}}^{2}$ .

This is about one-thirtieth of the acceleration of the Earth towards the Moon. The acceleration due to gravity on Earth, 9.81 m/s2, is about ^{107 times} greater.

Vertical and horizontal components of tidal acceleration

For the vertical and horizontal components of the tidal acceleration at any location on the Earth's surface that deviates from the Earth→Moon direction by angle θ as $\theta$ seen from the Earth's center, the following holds true

$a_{\text{v}}=-{\frac {G\cdot M\cdot r_{0}}{R^{3}}}(3\cdot \cos ^{2}\,\theta -1)$ for the vertical component and.

$a_{\text{h}}={\frac {3}{2}}\cdot {\frac {G\cdot M\cdot r_{0}}{R^{3}}}\cdot \sin \,2\theta$ for the horizontal component of the tidal acceleration.

The graph on the right shows the decomposition of tidal acceleration into components perpendicular and parallel to the earth's surface.

Calculation example - acceleration of the earth and tidal acceleration on its surface by the sun

With the constants

${\text{M}}=1{,}989\cdot 10^{30}\,{\text{kg}}$ for the mass of the sun, and

${\text{R}}=1{,}496\cdot 10^{11}\,{\text{m}}$ for the distance from the Sun,

results

$a_{\text{m}}=5{,}928\cdot 10^{-3}\,{\text{m}}/{\text{s}}^{\text{2}}$

for the gravitational acceleration of the earth originating from the sun, and

$a_{\text{g}}\approx \mp \ 5{,}048\cdot 10^{-7}\,{\text{m}}/{\text{s}}^{\text{2}}$

for tidal acceleration.

The tidal acceleration varies with the third power of the distance from the center of gravity and thus falls off faster than the gravitational acceleration, which varies quadratically. Although the Sun produces a gravitational acceleration at the location of the Earth that is almost 180 times greater than that of the Moon, the tidal acceleration it causes reaches only 46% of that caused by the Moon.

Superposition of the tidal forces caused by the moon and the sun

The tidal forces caused by the moon and the sun add up. The strongest total force occurs when the sun, earth, and moon are in alignment, which approximates at full and new moon with a period of about 14¾ days. Then they raise the water level of the ocean at high tide about ¾ meter (about ½ meter due to the moon and about ¼ meter due to the sun). At half moon, there is a right angle between the two force fields. Their superposition results in forces that raise the water level of the ocean less.

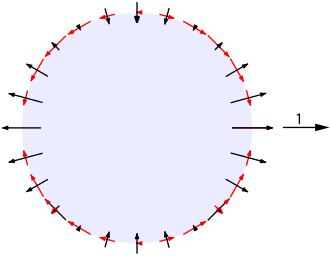
Decomposition of the locally different values of the tidal acceleration (or tidal force, see above graph) caused by the Moon into components. Arrow "1": Direction to the moon and axis of rotational symmetry.

Questions and Answers

Q: What is a tide?

A: A tide is the periodic rising and falling of Earth's ocean surface caused mainly by the gravitational pull of the Moon acting on the oceans.

Q: What changes do tides cause in the depth of marine and estuarine waters?

A: Tides cause changes in the depth of marine and estuarine (river mouth) waters.

Q: What are tidal streams?

A: Tidal streams are oscillating currents known as rip tides.

Q: Why is it important to predict the tide for coastal navigation?

A: Predicting the tide is important for coastal navigation because it can affect the depth of water and tidal streams.

Q: What is the intertidal zone?

A: The intertidal zone is the strip of seashore that is under water at high tide and exposed at low tide.

Q: Why is the intertidal zone an important ecological product of ocean tides?

A: The intertidal zone is an important ecological product of ocean tides because it provides habitat for many different species of plants and animals.

Q: How does the height of tides vary with the phases of the Moon?

A: The height of tides varies somewhat with the phases of the Moon. At New Moon and Full Moon, tides are higher because the Sun's tidal force adds to the Moon's. This is called "spring tide".