Thermodynamic potential

In thermodynamics, thermodynamic potentials are quantities whose information content fully describes the behavior of a thermodynamic system at equilibrium. The independent state variables of a thermodynamic potential are called its natural variables if their derivative of the potential is equal to one of the dependent state variables (for example: $\left(\partial U/\partial S\right)_{V,N}=T$ ). A thermodynamic potential corresponds from the information content to the internal energy whose natural variables S,V,N are all extensive (fundamental equation).

Thermodynamic potentials, which are energies, can be U(S,V,N) derived by Legendre transformation from the internal energy but unlike this they have one or more intensive quantities as natural variables $(T, p, \mu)$ . The intensive quantities arise in the coordinate transformation as derivatives of the internal energy according to their extensive variables.

In addition, there are other thermodynamic potentials that are not energies, for example, the entropy S(U,V,N) .

The notion of thermodynamic potential was generalized by Gottfried Falk to the notion of Massieu-Gibbs functions (after Josiah Willard Gibbs), which are corresponding state functions in not necessarily thermodynamic systems.

Physical meaning

An extreme value (not always a minimum) of a thermodynamic potential indicates thermodynamic equilibrium.

Thus, after the connection of one closed system to another, a thermodynamic equilibrium has been established as soon as the entropy of the total system is maximal. In this case, all intensive parameters of the two systems are also equal in each case:

$\begin{align} T_1 & = T_2\\ p_1 & = p_2\\ \mu_1 & = \mu_2 \end{align}$

Moreover, thermodynamic potentials summarize the equations of state of the system, since these are accessible by differentiating a thermodynamic potential according to its dependent variables.

Description

The internal energy U(S,V,N) and the functions arising from it by means of the Legendre transformation are thermodynamic potentials (except for the exception , see below). The Legendre transformation transforms the potentials

From entropy to temperature , since ∂ ${\frac {\partial U}{\partial S}}=T$
from volume to pressure , since ∂ ${\frac {\partial U}{\partial V}}=-p$
From particle number to chemical potential μ $\mu$ , since ∂ ${\frac {\partial U}{\partial N}}\,=\mu$

Given these 3 pairs of variables, there are 2^3 = 8 possible thermodynamic potentials:

Thermodynamic potentials
Name (alternative name)	Formula symbol	natural variables (intensive bold)	Characteristic function f	Interrelationships
Inner energy			${\mathrm d}U=TdS-pdV+\mu {d}N$	$U(S,V,N)=TS-pV+{\sum _{{i=1}}^{{K}}}\,\mu _{i}N_{i}.$ (Euler equation for internal energy).
Free energy (Helmholtz potential)		$\boldsymbol{T},V,N$	${\mathrm d}F=-SdT-pdV+\mu {d}N$
Enthalpy		$S,\boldsymbol{p},N$	${\mathrm d}H=TdS+Vdp+\mu {d}N$	$H=U(S,V,N)\qquad \ +pV$
Gibbs energy (Free enthalpy)		$\boldsymbol{T},\boldsymbol{p},N$	${\mathrm d}G=-SdT+Vdp+\mu {d}N$	${\begin{aligned}G&=U(S,V,N)-TS+pV\\&=H(S,p,N)-TS\\&=F(T,V,N)\qquad \quad +pV\end{aligned}}$
-		$S,V,\boldsymbol{\mu}$	${\mathrm d}R=TdS-pdV-N{d}\mu$	$R=U(S,V,N)\qquad \qquad \quad -\mu N$
Great Cannon Potential	$\Omega$	$\boldsymbol{T},V,\boldsymbol{\mu}$	${\mathrm d}\Omega =-S{d}T-p{d}V-N{d}\mu$	${\begin{aligned}\Omega &=U(S,V,N)-TS\qquad \ -\mu N\\&=R(S,V,\mu )-TS\\&=F(T,V,N)\qquad \qquad \quad -\mu N\end{aligned}}$
-		$S,\boldsymbol{p},\boldsymbol{\mu}$	${\mathrm d}J=TdS+Vdp-N{d}\mu$	${\begin{aligned}J&=U(S,V,N)\qquad \quad +pV-\mu N\\&=R(S,V,\mu )\qquad \quad +pV\\&=H(S,p,N)\qquad \quad \qquad -\mu N\end{aligned}}$
-		$\boldsymbol{T},\boldsymbol{p},\boldsymbol{\mu}$ Not useful, since the Gibbs-Duhem relation $T,p,\mu$ forbids the independent default of the variables	${\mathrm d}K=-SdT+Vdp-N{d}\mu$	${\begin{aligned}K&=U(S,V,N)-TS+pV-\mu N=0\\&=J(S,p,\mu )-TS\\&=\Omega (T,V,\mu )\qquad \quad +pV\\&=G(T,p,N)\qquad \quad \qquad -\mu N\end{aligned}}$

All meaningful thermodynamic potentials arising from U(S,V,N) by Legendre transformation provide the same complete information about a system. However, the simplest description of the system provides only one of the potentials, depending on the ensemble; this is extremal at equilibrium.

One way to remember the thermodynamic potentials with their natural variables is the Guggenheim square.

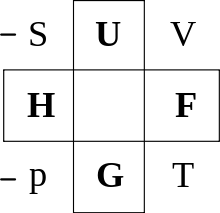
Guggenheim Square

Thermodynamic potential

Physical meaning

Description

Search by letter