Theoretical computer science
This is the sighted version that was marked on June 25, 2021. There is 1 pending change that needs to be sighted.
Theoretical computer science deals with abstraction, modelling and fundamental issues related to the structure, processing, transmission and reproduction of information. Its contents are automata theory, theory of formal languages, computability and complexity theory, but also logic and formal semantics as well as information, algorithm and database theory.
Theoretical computer science - by the proponents of this category of science - was placed in the structural sciences and provides foundations for the definition, verification and execution of the programs of programming languages, the construction of the compilers of programming languages - compiler construction - and the mathematical formalization and study of mostly discrete problems and their models. With the help of mathematical abstraction of properties of obtained models useful definitions, theorems, proofs, algorithms, applications and solutions of or to problems resulted. Theoretical computer science, with its timeless mathematical truths and methods, forms a formal skeleton that permeates computer science in practice with concrete implementations. Theoretical computer science identified many intractable problems by means of computability theory and, often with constructive proofs of complexity theory, allows the demarcation of problems that can be solved efficiently in practice from those for which the opposite is true.
The constructive methods of theoretical computer science also include the design of formal systems, automata, graphs and syntax diagrams as well as the definition of grammars and semantics in order to formally capture a problem with mathematical expressions and to distinguish it from the informal level. The constructs thus describe the inner logic of a problem with mathematical-logical statements, which subsequently allows a formal investigation and makes potentially new statements - supported by proofs - and algorithms of the formal models accessible as results. In addition to the mathematical gain in knowledge, some of the solutions found can be implemented practically to provide people with automated advantages of mathematics and computer use through machine semantics.
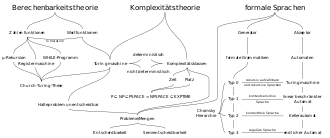
Mind map on a subarea of theoretical computer science
History of theoretical computer science
Theoretical computer science is closely related to mathematics and logic. In the 20th century, emancipation and formation as an independent discipline took place.
Pioneers of the discipline were Kurt Gödel, Alonzo Church, Alan Turing, Stephen C. Kleene, Claude Shannon, John von Neumann, Hans Hermes, and Noam Chomsky.
In 1936, the logician Heinrich Scholz requested (and received) a copy of Turing's seminal work On Computable Numbers, with an Application to the "Decision Problem". On the basis of this work, Scholz held (according to Achim Clausing) "the world's first seminar on computer science".
Automata theory and formal languages
Automata theory defines and formalizes automata or computing machines and deals with their properties and computational power. Among other things, automata theory investigates which problems can be solved by the different classes of computing machines.
The theory of formal languages considers formalized grammars and the formal languages generated by these grammars. It is concerned with syntactic and semantic features of these formal languages over an alphabet. The problem of whether a word belongs to a formal language is solved by automata; thus there is a close connection between the grammars that generate formal languages and the automata that recognize them.
Chomsky Hierarchy
Most formal languages encountered in practice, such as programming languages, have a simple structure and can be classified according to their complexity into one of the well-known language classes of the Chomsky hierarchy. The Chomsky hierarchy - after Noam Chomsky, a pioneer of language theory - consists of four classes. These are, in ascending order of power, the regular languages, (type 3), the context-free languages (type 2), the context-sensitive languages (type 1) and the recursively enumerable languages (type 0).
Regular languages can be derived from finite automata,
Context-free languages of (nondeterministic) basement automata,
context-sensitive languages of linearly constrained Turing machines and
recursively enumerable languages of general Turing machines are recognized.
There is equivalence between the four grammar classes and the four machine classes of the Chomsky hierarchy in terms of their generated and recognized classes of languages. The formal languages generated by the respective grammar classes of the Chomsky hierarchy can - as listed above - be recognized by the corresponding machine classes and vice versa.
Pumping and Jaffe lemmas
Well-known practical tools in the characterization of regular and context-free languages are the pumping lemmas, which provide a necessary but not sufficient condition that a language generated by a grammar is regular or context-free. Due to the structure of the statements of the lemmas, the pumping lemma for regular languages is also called uvw theorem and the pumping lemma for context-free languages is also called uvwxy theorem. Extensions like Jaffe's lemma provide a sufficient criterion in contrast to pumping lemmas.
Description of type 2 grammars
The Backus-Naur Form (after John W. Backus and Peter Naur) or BNF is a notational convention for context-free grammars and thus for context-free languages. The BNF is used in practice, for example, to define the syntaxes of programming languages. The respective syntaxes of the programming languages Pascal and Modula-2 have been defined in the extended Backus-Naur form, EBNF. The extended Backus-Naur form differs from the BNF only in some notational extensions.
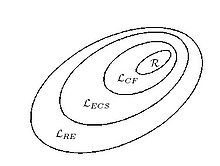
The language classes of the Chomsky hierarchy lie within each other as follows: Type 3 ⊂ Type 2 ⊂ Type 1 ⊂ Type 0, represented here by the inclusionsR ⊂ LCF ⊂ LECS ⊂ LRE.
Search within the encyclopedia