Adiabatic process

This article is about the thermodynamic term. For use in quantum mechanics, see Adiabatic theorem of quantum mechanics.

An adiabatic or adiabatic change of state (Greek α a, German 'nicht' and διαβαίνειν diabaínein 'to pass through') is a thermodynamic process in which a system is transferred from one state to another without exchanging heat with its surroundings. In this sense, adiabatic and 'heat-tight' are used interchangeably. The property of such a system of not exchanging heat with its surroundings is called adiabasia. In contrast, in diabatic and diathermic processes heat is exchanged with the environment (see for example: isothermal change of state).

Adiabatic changes of state, in which from the beginning to the end of the change at any time the system is almost in equilibrium, are called quasistatic, their course can be represented by a curve in the state space. If the quasistatic change of state is controlled solely by the change of external parameters of the system by means of idealized external devices, then these curves are called adiabatic. External parameters are quantities which describe the external, idealized constraints of the thermodynamic system; such as the volume of the system or the components of the magnetic field strength of an external magnetic field.

Thought experiments with adiabatic changes of state are fundamental for the determination of the postulates of thermodynamics. They provide the relationship between the work done on a system and the internal energy of the system. Carnot's cycle, often used in the thermodynamics literature, involves the adiabatic compression and expansion of the working gas. In the axiomatic structure of thermodynamics, adiabatic changes of state are of central importance. The conditions for adiabatic changes of state are never fully achieved in practice. However, this idealization provides useful to good descriptions for many real processes: for example, for rapidly occurring processes in which there is insufficient time for temperature equilibration, or for changes in systems in particularly thermally insulating containers.

Examples

The definition of adiabatic change of state given in the introduction covers many types of thermodynamic processes, including those which are not quasi-static. When reading various textbooks, a different impression can arise, since adiabatic changes of state are often considered there only in connection with quasi-static processes in simple systems.

According to the definition, in the case of an adiabatic change of state, energy may only be added to or removed from the thermodynamic system by means of mechanical, electrical or magnetic work; the system must be insulated against heat flows of any form; ideally, there must be no heat conduction, no convective heat transfer and no heat radiation between the system and the outside world.

In reality, complete thermal isolation is not achievable, but real processes can be adiabatic to a good approximation if

they take place in a well-insulated container, such as a Dewar vessel or an adiabatic calorimeter,
the change of state is so rapid that little heat can flow in or out in the short time (e.g. in a combustion engine, in an air pump or in sound propagation) or
the volume of the system is very large, so that heat flows at its edge play practically no role (e.g. in the case of thermally rising air parcels).

Compression and expansion of gases

The compression of air in an air pump is approximately an adiabatic change of state. The work done on the pump increases the internal energy of the air, and thus the temperature of the air also increases. With rapid repetitive compression, such as when inflating a bicycle tire, the increase in temperature at the pump can be readily felt. The additional internal energy is also colloquially known as compression heat or heat of compression.

With a pneumatic lighter, air is quickly compressed to less than one-twentieth of its original volume. The air becomes so hot that the stored tinder glows and can then be used to start a fire.

Conversely, if internal energy is converted into volume work during an expansion of a volume of air, the temperature of the expanding gas falls. The cooling of air masses during thermal uplift or during ascent at mountain edges is well known. Adiabatic expansion and thus cooling of the air also occurs on the upper surface of wings of commercial aircraft, see Dynamic lift. The cooling becomes visible when the saturation concentration, which decreases with temperature, falls below the existing humidity and cloud or fog formation occurs.

The Gay-Lussac experiment is also an adiabatic change of state. However, during the expansion of the gas, no internal energy is converted into external work. The process is not quasi-static; only at the beginning and end is the system in thermodynamic equilibrium. Ideal gases do not change their temperature during this process.

Friction

It is an adiabatic change of state when frictional work is performed on a thermally isolated system and the system is in thermodynamic equilibrium at the beginning and end of the work process.

The experimental procedure in the classical experiment to determine the heat equivalent by James Prescott Joule is one such process. Joule's system consisted of a copper tank with water and an integrated stirrer. Via the stirrer and a device with weights, a precisely measurable mechanical work was transformed into internal energy of the system (mainly water). Joule measured the temperature before and after the friction work. In his 1850 experimental report, he also discusses his arrangements for thermal insulation of the system.

Instead of a defined amount of mechanical work, a measured amount of electrical work $\int U(t)I(t)dt$ can also be performed on a system, for example to determine the heat capacity of a substance. The stirrer is replaced by an electric heater; the thermodynamic system consists of a container, the substance and the heater. For thermal isolation, the system is best located in a Dewar vessel or an adiabatic calorimeter. If the system is in thermodynamic equilibrium before and after the introduction of the electrical energy, this is an adiabatic change of state.

Electrochemical cell

An accumulator as a thermodynamic system can deliver energy in the form of electrical work to the outside or energy can be supplied to it by means of electrical work from the outside, depending on the direction of the current in the electrical supply lines. The supply or withdrawal of electrical energy leads to a change in the amounts of material at the electrodes. If the accumulator is thermally insulated by an adiabatic calorimeter in the process, adiabatic changes of state are involved. Since ohmic losses always occur during the process, the system heats up to a greater or lesser extent. Because of these ohmic losses alone, the change of state is not reversible. Such adiabatic changes of state are induced and measured, for example, during safety tests of batteries.

integration of systems

In thermodynamics, adiabatic changes of state are often considered, in which the initial state consists of two systems, each of which is in thermodynamic equilibrium. The two systems are considered as a single composite system. The change of state occurs when the systems are connected to each other without any work and then interact with each other; for example, through a thermal contact or by removing a partition between the systems - e.g. opening a separating valve. The processes involved are irreversible and can be very violent. The change is complete when the entire system no longer changes after the coupling, i.e. has found a new thermodynamic equilibrium.

In order for the change of state to be adiabatic the composite system must be thermally isolated from the environment, Dewar vessels or adiabatic calorimeters are suitable for this purpose. Some examples of such changes of state follow:

Determination of the heat of solution: One system consists of a known quantity of water and the other of a known quantity of common salt. Both systems have room temperature. Then the salt is added to the water - coupling of the systems. It dissolves in the water, then the temperature of the salt solution is measured.
Neutralization heat determination: Let one system be an acid and the other an alkali. Then the acid and alkali are carefully stirred together and the temperature of the mixture is followed until it does not change. From the temperature change and the amounts of substance, the heat of neutralization can be determined.
Chemical reaction: At the beginning a system of two moles of hydrogen and a system with one mole of oxygen are given. If a separating valve is opened between the two systems, an oxyhydrogen mixture is produced, which eventually reacts to form water. In the final state, the system consists of water.
Phases in equilibrium: One system is water in the liquid phase, the second is water vapour in a container. After a connection of the two systems, an equilibrium is established between the liquid and the gaseous phase.

Heat equalization between two systems

Let A and B be two simple systems, separated at the start of the process and each in thermal equilibrium. A has a higher temperature than B.

Irreversible heat balance: If the systems are pushed together so that they touch, or if they are thermally connected to each other via a copper wire, heat flows irreversibly from system A to system B until both systems have the same final temperature.
Reversible heat balance: If the heat energy is transported from the warmer to the colder system by an ideal heat engine - Carnot process - the temperatures of the systems approach each other. In this process, in addition to the heat transfer, work is done by the overall system, i.e. energy is extracted from it. If this process is repeated until the temperatures of the two systems are equal, the final temperature is lower than in the case of irreversible heat exchange, since the energy of the overall system has decreased, but the entropy has remained the same. Conversely, the temperature difference between systems A and B can also be increased again if, with the supply of external work, the machine between the systems is operated as a heat pump.

Fog formation in the negative pressure area of the wings of an aircraft

Joule's experimental set-up for the determination of the heat equivalent

Dewar vessel (Deutsches Museum, Munich)

Theory

An adiabatic change of state is a change of a thermodynamic system, isolated except for work processes, from an equilibrium state $z_{1}$ to an equilibrium state $z_{2}$ ; a mechanical or electrical work can be performed on the system from outside or it can perform such a work. If the work imparts energy to the system, then ; if the $W>0$ system performs work, then $W<0$ ; if no work is performed, then $W=0$ . It is important for the structure of thermodynamics that this definition of adiabatic change of state does not use the term heat.

Adiabatic accessibility

A state $z_{2}$ of a thermodynamic system is said to be $z_{1}$ adiabatically reachable from the state if there is an adiabatic change of state having $z_{1}$ as initial state and as $z_{2}$ final state.

For a thermodynamic system, the two postulates hold:

For each two equilibrium states $z_{1}$ and $z_{2}$ holds: $z_{2}$ is $z_{1}$ adiabatically reachable from or is reachable $z_{1}$ from $z_{2}$ .
If there are two adiabatic changes of state with the same initial state $z_{1}$ and the same final state $z_{2}$ , then the work $W_{1}$ of one state change is equal to the work the other.

For two states $z_{1}$ and $z_{2}$ , it may be that both $z_{2}$ $W_{1}$ is adiabatically reachable from $z_{1}$ with a work as well as $z_{1}$ of is $z_{2}$ W_2 adiabatically reachable with a work then $W_{2}=-W_{1}$ .

Definition of internal energy

Based on these postulates, it is possible to introduce the internal energy as a state function for a thermodynamic system. For any equilibrium state , $z_{0}$ a value is $U(z_{0})$ arbitrarily set. The internal energy for an arbitrary state is then obtained as follows:

if of $z_{0}$ is attainable by an adiabatic change of state with a work then $U(z)=U(z_{0})+W$ .
otherwise $z_{0}$ of must be reachable by an adiabatic change of state with a work and it is $U(z)=U(z_{0})-W$ .

The amount of heat as a physical quantity

The internal energy is fixed only up to a constant. With it, for a general change of state of a thermally non-isolated system from an initial state $z_{a}$ to a final state $z_{b}$ and a work , the heat supplied to the system in the process is given by

$Q=U(z_{b})-U(z_{a})-W$

is defined. For an adiabatic change of state, follows Q=0 .

Adiabatic changes of state are not only needed to define - as just shown - internal energy and heat as physical quantities, they can also be used to introduce temperature and entropy in the context of an axiomatic construction of thermodynamics. Two approaches are worth mentioning here:

Axiomatic models

The mathematician Constantin Carathéodory, in his study of the foundations of thermodynamics, makes the statement:

"In any given neighborhood of an arbitrarily prescribed initial state, there are states that cannot be arbitrarily approximated by adiabatic changes of state."

as an axiom at the beginning of a mathematical model for thermodynamic systems. This axiom is equivalent to the second law of thermodynamics.

Carathéodory introduces in his work the notion of a simple thermodynamic system: it is a system in which each equilibrium state is uniquely determined solely by the specification of a value for the internal energy and a tuple of external parameters $V_{1},\dots ,V_{m}$ for the external constraints.

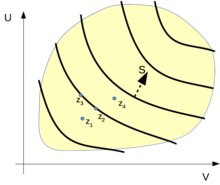
In a recent paper on the second law of thermodynamics, Elliot H. Lieb and Jakob Yngvason develop a mathematical model for thermodynamic systems without the implicit assumptions made by Caratheodory about analytical properties of the state functions. This model is based on the quasi-order in the state space given by the adiabatic reachability; see also the accompanying schematic drawing. A presentation in German with illustrative application examples can be found in a textbook by André Thess.

With supplementary axioms for the scaling and coupling of thermodynamic systems Lieb and Yngvason define for equilibrium states the state function of entropy and only over this the temperature. Monotonicity S(z) holds for the entropy : in a simple thermodynamic system, an equilibrium state is $z_{2}$ $z_{1}$ adiabatically reachable from a state exactly when $S(z_{2})\geq S(z_{1})$ .

Schematic representation of the state space of a simple thermodynamic system - thick lines show hypersurfaces with constant entropy, the arrow shows the direction of increasing entropy - The state $z_{2}$ is $z_{1}$ adiabatically reachable from but not $z_{1}$ from $z_{2}$ . - Both $z_{3}$ is $z_{2}$ adiabatically reachable from and conversely is reachable $z_{2}$ from $z_{3}$ .