Tetration

In mathematics, especially number theory, one speaks of a power tower when the exponent of a power is itself represented as a power. This can then be repeated in that the exponent of the exponent is also a power, and so on, so that the bases build up into a tower terminated by the (final) exponent. The notation is usually used for numbers where the exponent would be too large in normal notation, for example:

$2^{{1.267.650.600.228.229.401.496.703.205.376}}=2^{{2^{{100}}}}$

The larger the number becomes, the clearer the advantage of this abbreviated notation becomes.

$2^{2^{2^{2^{2^{2}}}}}=2^{2^{2^{2^{4}}}}=2^{2^{2^{16}}}=2^{2^{65.536}}$

Already the exponent of this power of 2, written in decimal notation, would have 19,728 digits. The total result would thus hardly be usable or understandable.

The convention is that power towers are processed "from top to bottom", i.e. starting with the highest power:
$2^{3^{4}}$ therefore means $2^{\left(3^{4}\right)}=2^{81}$ and not $\left(2^{3}\right)^{4}=8^{4}=2^{12}$ .

With the help of this notation, very large numbers can be clearly represented, which quickly lie beyond any direct imaginability and which can no longer be represented in absolute length and as a simple power, or only in a cumbersome way.

Nevertheless, there are numbers that are so large that even this notation is no longer sufficient to represent them. So if a power tower has too many levels to be represented, one uses alternative notations like the hyper-operator.

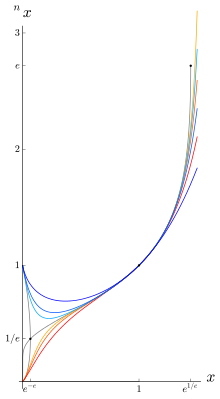
x↑↑a for a = 2,3,4,5,6,7 and limits for a towards infinity (gray).

Representation with sequences and infinite power towers

A finite power tower of the form (see also arrow notation)

${\begin{matrix}x\uparrow \uparrow n&=&\underbrace {x^{x^{{}^{.\,^{.\,^{.\,^{x}}}}}}} \\&&n{\mbox{ Kopien von }}x\end{matrix}}$

where $x\in {\mathbb R}^{{\geq 0}}$ and $n\in \mathbb {N}$ coincides with the -th member $a_{n}(x)$ of the equation given by

$a_{{n}}(x):={\begin{cases}x,&{\text{falls }}n=1\\x^{{a_{{n-1}}(x)}},&{\text{falls }}n>1\end{cases}}$

recursively defined sequence $(a_{{n}}(x))$ This is called a partial tower sequence and is identified with the infinite power tower (analogous to the notion of infinite series).

If is $(a_{{n}}(x))$ convergent with the limit A(x), then the (infinite) power tower is called convergent with

$x\uparrow \uparrow \infty =x^{x^{{}^{.\,^{.\,^{.\,}}}}}=A(x).$

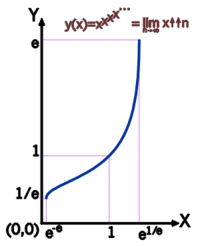
Already Leonhard Euler has recognized that the power tower

$x\uparrow \uparrow \infty =x^{x^{{}^{.\,^{.\,^{.\,}}}}}\qquad {\text{f}}{\ddot {\text{u}}}{\text{r}}\;x\in \mathbb {R} ^{\geq 0}$

converges exactly when

$0{,}065988\approx {\frac {1}{e^{e}}}=e^{-e}\leq x\leq e^{\frac {1}{e}}\approx 1{,}444668.$

The function defined by this

$A\colon [e^{-e},e^{\frac {1}{e}}]\to [{\tfrac {1}{e}},e],\quad A(x)=x^{x^{{}^{.\,^{.\,^{.\,}}}}}$

is strictly monotonically increasing and bijective. Its inverse function is given by

$A^{-1}\colon [{\tfrac {1}{e}},e]\to [e^{-e},e^{\frac {1}{e}}],\quad A^{-1}(x)=x^{\frac {1}{x}}$ .

Tetration

Representation with sequences and infinite power towers

See also

Search by letter