Tesseract
![]()
This article explains the four-dimensional cube; for the meanings of the word tesseract, see there.
The tesseract [ˈtɛsərakt] (from ancient Greek τέσσερες ἀκτίνες tésseres aktínes, German 'four rays') is a transfer of the classical concept of a cube to four dimensions. It is also referred to as a four-dimensional hypercube. The tesseract relates to the cube like the cube to the square. It has 16 corners, 32 edges of equal length, 24 square faces, and is bounded by 8 cube-shaped cells. These cells are also called bounding cubes of the tesseract. In each corner 4 edges, 6 faces and 4 cells meet each other perpendicularly.
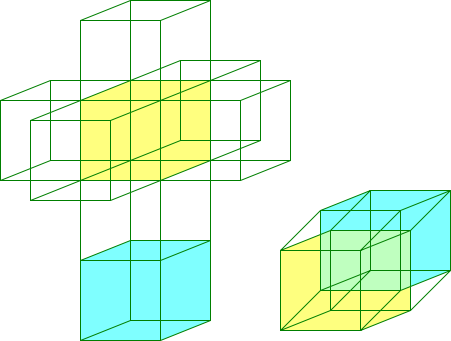
The pictures in this article are to be understood as pictures of tesseracts under parallel projections. At the bottom of the right image, one can see a blue and a yellow cube connected by six more rhombohedrically distorted bounding cubes. In the three-dimensional mesh of the tesseract (left in the first picture), all eight bounding cubes are folded into three-dimensional space, just as the faces of a three-dimensional cube can be unfolded into a mesh of six squares. There are 261 ways to unfold a tesseract.
The following image shows a mesh of the tesseract on the left, and a two-dimensional parallel projection of the tesseract on the bottom right.
The longest diagonal of a hypercube is equal to the square root of its number of dimensions multiplied by its edge length. In a tesseract, the longest diagonal is therefore two edge lengths long. In a tesseract, if you interlock its eight opposite bounding cubes in pairs, you get a 4-torus.
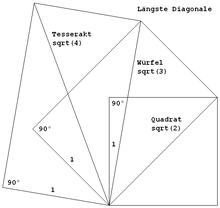
The construction of the longest diagonals of the square, cube and tesseract
Projections in two dimensions
The construction of a hypercube can be imagined as follows:
- one-dimensional: Two points A and B can be connected to a line, a new line AB is created.
- two-dimensional: two parallel lines AB and CD of equal length can be connected to form a square, with corners ABCD.
- three-dimensional: two parallel squares ABCD and EFGH of equal area can be connected to form a cube, with corners ABCDEFGH.
- four-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP with the same volume can be connected to form a hypercube, with corners ABCDEFGHIJKLMNOP.
It is difficult to imagine, but possible to project tesseracts into three- or two-dimensional spaces. Moreover, projections into the second dimension become more revealing if one rearranges the projected vertices. Using this method, one can obtain images that no longer reflect the spatial relationships within the tesseract, but do reflect the connecting structure of the vertices, as the following examples show:
In principle, a tesseract is formed by two connected cubes. The scheme is similar to the construction of a cube of two squares: one places two copies of the lower dimensional cube next to each other and connects the corresponding vertices. Each edge of a tesseract is of the same length. Eight cubes connected to each other.
Tesseracts are also bipartite graphs, just like lines, squares, and cubes.
Projections in three dimensions
The cell-first parallel projection of the tesseract into three-dimensional space has a cube-shaped envelope. The nearest and farthest faces are projected onto the cube and the remaining 6 cells are projected onto the square faces of the cube.
The surface-first parallel projection of the tesseract into 3-dimensional space has a cuboidal hull. Two pairs of the cells project the upper and lower half of the hull and the 4 remaining cells are projected onto the side faces.
The edge-first parallel projection of the tesseract into three-dimensional space has a hull in the form of a hexagonal prism. Six cells are projected onto rhombic prisms laid out in the hexagonal prism, analogous to how the faces of a 3D cube are laid out on a hexagonal hull in the edge-first projection. The two remaining cells are projected onto the bases of the prism.
The corner-first parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedral hull.
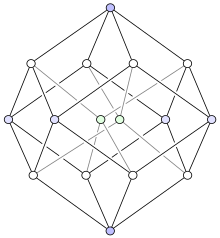
The rhombic dodecahedron forms the shell of this projection of a tesseract in 3 dimensions
Search within the encyclopedia