Skip to content
Home

Subset (mathematics)

Explanation of subsets: definitions, notation, examples, properties and distinctions such as proper subset and relation to power sets, aimed at a general mathematical audience.

Author: Created: Updated:

A subset is a fundamental concept in set theory and everyday mathematics. Informally, a set A is called a subset of a set B when every element of A also belongs to B. This relationship is written A ⊆ B. When A contains some but not all elements of B, A is a proper (or strict) subset of B and is often written A ⊂ B. The empty set Ø is a subset of every set, while every set is a subset of itself.

Image gallery

1 Image
Socrates
en.wikipedia.org · Public domain

Definitions and notation

Key terms and symbols used with subsets include:

  • Subset (non-strict): A ⊆ B means ∀x(x ∈ A ⇒ x ∈ B).
  • Proper subset (strict): A ⊂ B means A ⊆ B and A ≠ B.
  • Not a subset: A ⊄ B indicates there exists an element of A not in B.
  • Superset: B ⊇ A is equivalent to A ⊆ B; B ⊃ A corresponds to A ⊂ B.

Examples

Concrete examples make the idea clear. If B = {1, 2, 3}, then A = {1, 2} satisfies A ⊂ B, while C = {1, 2, 3} satisfies C ⊆ B but not C ⊂ B. The set Ø is a subset of B and of every other set. Subsets can be finite or infinite; for instance, the set of even integers is a subset of the integers.

The subset relation is reflexive (A ⊆ A for every A) and transitive (if A ⊆ B and B ⊆ C then A ⊆ C), making it a partial order on the collection of all subsets of a given set. The collection of all subsets of a set S is called the power set of S and is denoted P(S); its elements are precisely the subsets of S. Cardinality interacts with inclusion: if A ⊂ B then |A| ≤ |B|, with strict inequality when both are finite and A ≠ B.

Uses, distinctions and remarks

Subsets are used throughout mathematics to form substructures (subgroups, subspaces, suborders), to specify domains and constraints, and to reason about containment. Be aware that notation varies: some authors use ⊂ to mean non-strict subset (same as ⊆), while others reserve ⊂ for strict inclusion. When precision matters, the words "proper" or explicit equality checks help avoid ambiguity. For further reading on foundational ideas see general resources on sets.

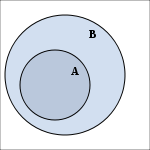
Set diagram: A is a (real) subset of B.
Set diagram: A is a (real) subset of B.

Definition

If Aand Bare sets and each element of Aalso an element of B, then Acalled a subset or subset of B:

A \subseteq B :\Longleftrightarrow \forall x \in A\colon x \in B

Conversely, Bcalled the superset of Aexactly when is subset of AB

B \supseteq A :\Longleftrightarrow A \subseteq B

Furthermore, there is the notion of a real subset. Ais a real subset of Bexactly if Aa subset of Band is Anot identical to }B.

{\displaystyle A\subsetneq B:\Longleftrightarrow A\subseteq B\land A\neq B}

Again, one also writes B \supsetneq Aif A \subsetneq B.

Other notations

⊂⊊⊆⊇⊋⊃

Some authors also use the characters \subset and \supset for subset and superset instead of \subseteq and \supseteq. Mostly the author then does not define the term "real subset".

Other authors prefer the characters \subset and \supset for true subset and superset thus instead of \subsetneqand \supsetneq. This usage is fittingly reminiscent of the characters for inequality ≤ \leq and <. Since this notation is mostly used when the difference between real and non-real subsets is important, the characters \subsetneqand \supsetneqrather rarely used.

Variants of the character \subsetneqare also \varsubsetneq , \subsetneqq and \varsubsetneqq . If is Anot a subset of B, can also be A\nsubseteq B :\Longleftrightarrow \lnot \left(A\subseteq B\right)used. Corresponding notations are \varsupsetneq for \supsetneq, \supsetneqq and \varsupsetneqq for \supsetneq, and {\displaystyle A\nsupseteq B}(no superset).

The corresponding Unicode symbols are: ⊂, ⊃, ⊆, ⊇, ⊄, ⊅, ⊈, ⊉, ⊊, ⊋ (see: Unicode block Mathematical Operators).

Speech

Instead of " Ais a subset of B." we also say "The set ABcontained in the set " or "The set Ais Bcontained by ." said. Similarly, instead of saying " Bis a superset of A.", we say "The set Bcontains the set A." or "The set Bcontains the set A.". If there can be no misunderstanding, " Bcontains A." etc. is also said. Misunderstandings can arise in particular with "The set Bcontains the element A.".

Examples

  • {1, 2} is a (real) subset of {1, 2, 3}.
  • {1, 2, 3} is a (fake) subset of {1, 2, 3}.
  • {1, 2, 3, 4} is not a subset of {1, 2, 3}.
  • {1, 2, 3} is not a subset of {2, 3, 4}.
  • {} is a (real) subset of {1, 2}.
  • {1, 2, 3} is a (real) superset of {1, 2}.
  • {1, 2} is a (fake) superset of {1, 2}.
  • {1} is not a superset of {1, 2}.
  • The set of prime numbers is a real subset of the set of natural numbers.
  • The set of rational numbers is a real subset of the set of real numbers.

More examples as set diagrams:

·        

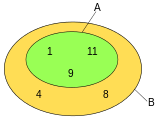
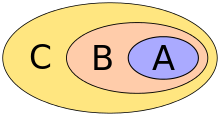
A is a real subset of B

·        

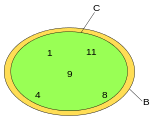
C is a subset of B, but not a real subset of B

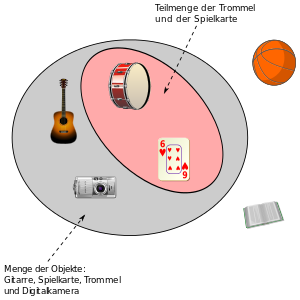
The set {drum, playing card} is a subset of the set {guitar, playing card, digital camera, drum}
The set {drum, playing card} is a subset of the set {guitar, playing card, digital camera, drum}
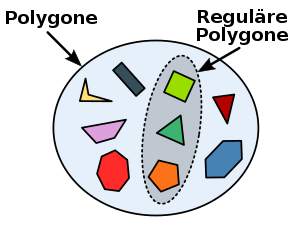
The regular polygons form a subset of the set of all polygons.
The regular polygons form a subset of the set of all polygons.

Properties

\varnothing \subseteq A

  • Every set is a subset of itself:

A \subseteq A

  • Characterization of inclusion with the help of the association:

A \subseteq B \Leftrightarrow A \cup B = B

  • Characterization of inclusion using the average:

A \subseteq B \Leftrightarrow A \cap B = A

  • Characterization of inclusion using the difference set:

A \subseteq B \Leftrightarrow A \setminus B = \varnothing

  • Characterization of inclusion using the characteristic function:

A \subseteq B \Leftrightarrow \chi_A \le \chi_B

  • Two sets are equal if and only if each is a subset of the other:

{\displaystyle A=B\Leftrightarrow A\subseteq B\land B\subseteq A}

This rule is often used when proving equality of two sets by showing mutual inclusion (in two steps).

  • In the transition to complement, the direction of inclusion reverses:

A \subseteq B \Rightarrow A^{\rm c} \supseteq B^{\rm c}

  • When forming the intersection, you always get a subset:

A \cap B \subseteq A

  • When forming the union set, you always get a superset:

A \cup B \supseteq A

Inclusion as order relation

Inclusion as a relation between sets satisfies the three properties of a partial order relation, namely it is reflexive, antisymmetric and transitive:

A \subseteq A

A \subseteq B \subseteq A \Rightarrow A = B

A \subseteq B \subseteq C \Rightarrow A \subseteq C

(Where A\subseteq B\subseteq Ca shorthand notation for A\subseteq Band B\subseteq C.)

Thus, if M \,a set of sets (a set system), then (M, \subseteq) a half-order. In particular, this holds for the power set \mathcal P(X) a given set X.

If A ⊆ B and B ⊆ C, then also A ⊆ C
If A ⊆ B and B ⊆ C, then also A ⊆ C

Inclusion Chains

If is M \,a set system such that of every two sets occurring in M \,one includes or is included by the other, such a set system is called an inclusion chain. An example of this is provided by the system \{{]{-\infty, x}[} \mid x \in \R \}of the left unconstrained open intervals of \mathbb {R} .

A special case of an inclusion chain exists if a (finite or infinite) set sequence is given which is ordered by \subseteq ascending or by \supseteq descending. One writes then briefly:

A_1 \subseteq A_2 \subseteq A_3 \subseteq \ ...

A_1 \supseteq A_2 \supseteq A_3 \supseteq \ ...

Size and number of subsets

  • Every subset of a finite set is finite and for the powers holds:

A \subseteq B \Rightarrow \left| A\right| \le \left| B\right|

A \subsetneq B \Rightarrow \left| A\right| < \left| B\right|

  • Every superset of an infinite set is infinite.
  • The same applies to the thicknesses for infinite sets:

A \subseteq B \Rightarrow \left| A\right| \le \left| B\right|

  • For infinite sets, however, it is possible for a real subset to have the same power as its base set. For example, the natural numbers are a real subset of the integers, but the two sets are equally powerful (namely, countably infinite).
  • By Cantor's theorem, the power set of a set Aalways more powerful than the set Aitself:
  • A finite set with nelements has exactly 2^{n}subsets.
  • The number of k-elementary subsets of an n-elementary (finite) set is {\tbinom {n}{k}}given by the binomial coefficient

See also

  • characteristic function

Related articles

Author

AlegsaOnline.com Subset (mathematics)

URL: https://en.alegsaonline.com/art/94508

Share