String theory

String theory is a collection of closely related hypothetical physical models which, instead of describing elementary particles in the usual models of quantum field theory as point-like particles (spatial dimension zero) in space-time, use so-called strings as fundamental objects with one-dimensional spatial extension. In extensions of string theory, higher-dimensional objects are also considered. String theories were introduced in the 1960s to describe the strong interaction (quantum chromodynamics).

Since the 1980s, string theory has experienced a strong upswing. Since then, it has been regarded as the dominant candidate for a theory that unifies all forces of nature and combines the Standard Model of elementary particle physics and gravitation. The main subject of discussion is the supersymmetric version of string theory ("superstring theory"). Supersymmetry predicts new, supersymmetric partner particles for all bosons and fermions. A major contribution to the appreciation of superstring theory was that it made concrete predictions for the symmetry groups of a Grand Unified Theory (GUT). In the 1990s, it turned out that the hitherto known superstring theories and 11-dimensional supergravity could be considered together as part of a more comprehensive theory ("M-theory"). The latter also includes higher-dimensional objects (so-called "brane").

String theory led to an unprecedentedly close exchange between different fields of mathematics and theoretical physics, resulting in fundamental new insights, and to upheavals in the way quantum field theories (such as the holographic principle in AdS/CFT) are viewed. Strings have also found applications in other areas of physics, such as the description of excitations in solid state physics and the theory of strong interactions (quantum chromodynamics).

String theory is currently neither experimentally confirmed nor refuted. One of the reasons for this is that the unification of the forces of nature is only expected at energy scales (see Planck scale) which are not achievable in the foreseeable future. String theory has therefore been criticized since the 2000s, both within and outside of physics. Criticism has also been directed at the one-sided and extraordinary commitment of research resources in areas remote from applications, and has been particularly determined by theorists pursuing alternative theories of quantum gravity (such as loop quantum gravity). Moreover, an unexpected number of variants emerged in the concrete mathematical workout of string theory, making the prospects of success in unifying all forces of nature via string theory a distant prospect.

Overview

In contrast to the standard model of particle physics, in string theory the fundamental building blocks that make up the world are not particles in the sense of points (i.e. zero-dimensional objects), but vibrating one-dimensional objects. These one-dimensional objects are called strings. Elementary particles can be thought of as vibrational excitations of the strings, with the frequency corresponding to an energy according to quantum mechanics.

In further developments of string theory, the so-called brane theories, not only one-dimensional (or, if time is included, (1+1)-dimensional) strings are considered as basic objects, but also higher-dimensional objects ("brane") are used.

By assuming this one-dimensional structure of strings, many desirable properties of a more fundamental theory of physics automatically emerge. What stands out most is that any string theory compatible with quantum mechanics must include quantum gravity.

In string theory, problems arising from divergent loop integrals and the renormalization theories developed to compensate them are avoided. Divergences (infinite values of the integrals) arise specifically for point particles from their self-interaction, which is "smeared" and thus mitigated for extended, e.g. one-dimensional, objects. Simplified, one can imagine it like this: If one considers the Heisenberg uncertainty relation Δ fundamental to quantum mechanics. , we observe that if Δ , then Δ . This means that if the distance vanishes, there would be an infinite momentum. Now in string theory the case Δ is avoided and there exists an upper bound, the momentum can only have a large but finite value, in this way the divergences in the theory are avoided. The uncertainty relation for strings is modified to

with α,

Where describes the string tension. The new term α is used here to specify a minimum distance. This minimum distance is now given by:

Now if αholds, the problem of point interactions does not arise because they are excluded.

The characteristic length scale of strings would have to be of the order of the Planck length, the size below which effects of quantum gravity become important:

On much larger length scales, such as those accessible in laboratories today, these objects would be indistinguishable from zero-dimensional point-like particles. Nevertheless, the vibrational states and structure of these tiny strings would make them appear as different elementary particles of the Standard Model of elementary particle physics. For example, one vibrational state of the string would be associated with a photon, another state with a quark. This unifying effect of string theory is one of its greatest strengths, but no known solution of this theory yet reproduces exactly the variety of particles known to the Standard Model.

In space-time, a particle sweeps across a line called the world line: The particle has no spatial extent, but it moves along "time". A string, on the other hand, has a two-dimensional world surface ("world sheet"), since it also has a spatially one-dimensional extension. The interactions of elementary particles, described in the usual quantum field theory of point particles with Feynman diagrams in space-time, can be imagined by "thickening" these Feynman diagrams in one direction of space (see above picture).

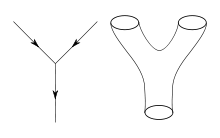
Interactions in the subatomic realm: world lines of point particles in the Standard Model and the analogous world surfaces in string theory


Strings as building blocks of the universe - a hierarchy: from macroscopic objects to atoms, nuclei, quarks or gluons and "strings

Types of strings

Closed and open strings

Strings can be either open or closed. A "closed string" has no endpoints and is therefore topologically equivalent to a circle. An "open string" has two ends and is topologically equivalent to a stretch. Not all string theories contain open strings, but every theory must contain closed strings, since interactions of open strings can always produce closed ones.

The oldest string theory that contained open strings was the type-1 string theory.

Both open and closed strings are always associated with characteristic types of vibration (modes). A particular vibration of a closed string can be identified as a graviton. In certain string theories, the vibration with the lowest energy of an open string represents a tachyon. Other vibrational modes of open strings exhibit the properties of photons or gluons.

Orientation

Strings can also have an "orientation", which can be thought of as a string-internal arrow that distinguishes them from strings with the opposite orientation. In contrast, there is also the "non-oriented string", to which no such arrow can be assigned.