Stress (mechanics)

The mechanical stress (formula symbols σ (small sigma) and τ (small tau), English stress, French contrainte) is a measure of the internal stress of a body due to its external load. Since there is no danger of confusion with electrical stress within mechanics, it is referred to as stress for short.

The normal mechanical stress σ on an imaginary area A through a body is the component Fn of an external force F acting perpendicularly on it:

$\sigma =\lim _{\Delta A\to 0}{\frac {\Delta F_{n}}{\Delta A}}$ .

The definition of the stress term goes back to Cauchy (1823).

The mechanical shear stress τ in an imaginary sectional surface A through a body is the component _FA (transverse force) of an external force F running in it:

$\tau ={\frac {F_{A}}{A}}$ , (approximate equation: shear stress is not constant over surface and is always zero at surface boundary).

Mechanical stress has the same physical dimension as pressure, namely force per unit area. In liquids and gases at rest, pressure is a normal stress acting equally in all spatial directions.

In mechanical and structural engineering, the dimensioning of objects requires knowledge of the occurring mechanical stresses. As components of the stress tensor, the mechanical stresses occur in physical laws.

Interface voltages

→ Main article: Cut reaction

By applying the principle of sectioning, internal stresses of a body can be graphically represented. At an imaginary section at any point of a body, the section forces are applied, which result from the forces acting on the body from the outside and allow the conclusion to be drawn about the internal stresses of the body.

Normal stress, bending stress, shear stress, torsional stress and true stress

For a uniform tensile or compressive load on a bar, the stress is uniformly distributed over the cross-sectional area. The normal stress, i.e. the stress under normal force loading due to tension or compression, is given by

$\sigma _{N}={\frac {F}{A}},$

where $F=F_{\perp }$ is the force in the direction of the surface normal and the area of the bar cross-section. For true stresses this is the area in the deformed member and for nominal or engineering stresses it is the nominal value of the undeformed initial member cross section, see tensile test. The stress tensor always has 3 (for all three spatial directions) normal stress components, if this is positive in one spatial direction, tension is present in this spatial direction, likewise with compressive stresses, the normal stress component is then negative in this direction.

When the bar is subjected to a bending load, a bending stress results which is highest at the edge of the bar cross-section (in the so-called edge fibre) and decreases to zero towards the centre (in the so-called neutral fibre). In summary, the bending stress is the compressive and tensile stress caused by the bending in one part of the cross-section at a time:

$\sigma _{B}(x,y,z)=-{\frac {M_{z}(x)\cdot I_{y}+M_{y}\cdot I_{yz}}{I_{y}(x)\cdot I_{z}(x)-(I_{yz})^{2}}}\cdot y+{\frac {M_{y}(x)\cdot I_{z}(x)+M_{z}(x)\cdot I_{yz}}{I_{y}(x)\cdot I_{z}(x)-(I_{yz})^{2}}}\cdot z$

With constant uniaxial bending $M_{y}(x)=M_{y}$ in the principal inertial axis system, the formula simplifies to:

$\sigma _{B}(z)={\frac {M_{y}}{I_{yy}}}\cdot z\quad {\text{und}}\quad |\sigma _{B}|_{\mathrm {max} }={\frac {|M_{y}|}{|W_{y}|_{\mathrm {min} }}}\quad {\text{mit}}\quad W_{y,{\text{positiv}}}={\frac {I_{yy}}{z_{\mathrm {max} }}}\quad {\text{und}}\quad W_{y,{\text{negativ}}}={\frac {I_{yy}}{z_{\mathrm {min} }}},$

where $M_{y}$ is the bending moment about the y-axis, $I_{yy}$ is the plane moment of inertia about the y-axis, is the distance from the neutral fiber (for σB = 0), $z_{R}$ is the maximum or minimum occurring distance from the axis of gravity to the edge fiber, and is the section modulus, see beam theory. The following sketch illustrates this on a cantilever beam:

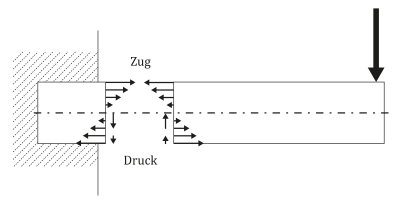
Spannungen in Kragträger

As a vector, the section stress vector has three components that depend on the orientation of the section face. The vertical arrows on the cut edges indicate shear stresses introduced by the shear force. In the case of a profile loaded with a shear force, as shown in the figure, a non-constant shear stress curve occurs across the cross-section. If the shear force acts outside the shear center, torsion also occurs.

In the case of torsion of bars with circular (ring) cross-section, the shear stress is:

$\tau ={\frac {M_{t}}{I_{p}}}r\quad {\text{und}}\quad \tau _{\mathrm {max} }={\frac {M_{t}}{W_{t}}}\quad {\text{mit}}\quad W_{t}:={\frac {I_{p}}{r_{a}}}$

Where _Mt is the torsional moment, Ip is the polar moment of area inertia, Wt is the torsional moment of resistance, r is the radial cylinder coordinate and _ra is the outer radius of the (hollow) cylinder.

The formulas for bending and torsional stress assume linear elasticity.

The tensor calculation allows to describe the stress state at first independent of a certain coordinate system and to adapt it to the geometrical properties of the body only after deriving the respective calculation method (like the formulas above), for example in cylindrical coordinates as in torsion.

Questions and Answers

Q: What is stress?

A: Stress is the force per unit area on a body that tends to cause it to change shape. It is a measure of the internal forces in a body between its particles, and is the average force per unit area that a particle of a body exerts on an adjacent particle across an imaginary surface that separates them.

Q: How do external forces affect stress?

A: External forces are either surface forces or body forces, and they cause deformation of the body's shape which can lead to permanent shape change or structural failure if the material is not strong enough.

Q: What is the formula for uniaxial normal stress?

A: The formula for uniaxial normal stress is σ = F/A, where σ is the stress, F is the force and A is the surface area. In SI units, force is measured in newtons and area in square metres, meaning stress would be newtons per square meter (N/m2). However, there exists its own SI unit for stress called pascal (Pa), which equals 1 N/m2. In Imperial units, it would be measured in pound-force per square inch (psi).

Q: What does continuum mechanics assume about force?

A: Classical models of continuum mechanics assume an average force and do not properly include geometrical factors - meaning they don't take into account how geometry affects how energy builds up during application of external force.

Q: How can different models give different results when looking at deformation of matter and solid bodies?

A: Different models look at deformation of matter and solid bodies differently because characteristics of matter and solids are three dimensional - so each approach takes into account different aspects which can lead to varying results.

Q: How does continuum mechanics treat loaded deformable bodies?

A: Continuum mechanics treats loaded deformable bodies as continua - meaning internal forces are distributed continually within volume of material body instead being concentrated at certain points like with classical models.