Squaring the circle

The title of this article is ambiguous. For other meanings, see Squaring the circle (disambiguation).

The squaring of the circle is a classical problem in geometry. The task is to construct a square with the same area from a given circle in finitely many steps. It is equivalent to the so-called rectification of the circle, that is, the construction of a straight line equal to the circumference of the circle. This, in turn, is equivalent to constructing the circumference π $\pi$ (half the circumference of the circle) from the distance whose length is equal to unit of length. If one restricts the means of construction to a ruler and compasses, the problem is $\pi$ unsolvable due to the transcendence of π {\displaystyle It was not until 1882 that this could be proved by the German mathematician Ferdinand von Lindemann.

Squaring the circle is one of the most popular problems in mathematics. For centuries, not only mathematicians but also laymen searched in vain for a solution. The term squaring the circle has become a metaphor for an unsolvable problem in many languages.

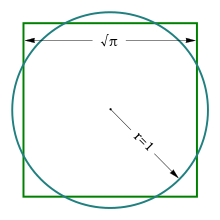
The square and the circle have the same area.

Popularity of the circle quadrature

The squaring of the circle, like only a few other problems, also achieved great popularity outside mathematics. As a result, many mathematical laymen tried to solve the seemingly simple problem; some thought they had found it.

Reports of a growing emergence of amateur work from the 18th and 19th centuries and examples on the subject can be found in Jean-Étienne Montucla, Johann Heinrich Lambert and Augustus de Morgan. As a rule, these were procedures in which the problem was solved "exactly" mechanically, numerically, or by a geometric approximate construction. Such work was brought to the attention of mathematicians or scientific institutions in such large numbers that, for example, the Paris Academy of Sciences felt compelled in 1775 to officially reject further investigation of pretended solutions to the quadrature of the circle:

" L'Académie a pris, cette année, la résolution de ne plus examiner aucune solution des problèmes de la duplication du cube, de la trisection de l'angle ou de la quadrature du cercle, ni aucune machine annoncée comme un mouvement perpétuel. »

"The Academy has this year taken the decision not to investigate in the future the solutions of mathematical problems concerning the doubling of the cube, the tripartition of the angle, and the squaring of the circle, nor any machine claiming to be a 'perpetual motion machine.'"

Even after Lindemann's proof of impossibility in 1882, supposed circular quadratures were still being published in the 20th century, and in more recent times they have become the stuff of entertainment mathematics as futile attempts by amateur mathematicians.

A main reason for the high attractiveness especially for mathematical laymen is probably the very elementary problem, which can be understood or at least seems to be understandable even without deeper mathematical knowledge. Together with the numerous unsuccessful attempts by established scientists to solve the problem, the circle quadrature acquired a real aura.

Another reason for the numerous efforts to square the circle, which should not be underestimated, was the widespread opinion that a high prize was offered for solving the problem - a misconception that may have been based on the erroneous assumption that squaring the circle was directly connected with the problem of determining the exact longitude to sea, which had also remained unsolved for a long time and for which prizes were indeed offered. The legend of the prize competitions was so persistent that even in 1891 it could be read in Meyer's Konversations-Lexikon that "Charles V had offered 100,000 Thaler and the Dutch States General an even higher sum".

Prominent circle squares

A prominent example of an amateur mathematician who thought he had squared the circle was the English philosopher Thomas Hobbes. His solution, published in 1665 in his work De corpore - in reality an approximate construction - was refuted by John Wallis in the same year. Subsequently, the two engaged in an acrimonious dispute that only ended with Hobbes's death in 1679.

Lambert reports three circle squares by means of a certain rational value. The works published in the middle of the 18th century are based on the approximation ^35/31 for the ratio of the diameter of the circle to the side of the equal area square. For the circle number one receives from it the approximation

$\pi \approx {\frac {3844}{1225}}=3{,}1{\color {red}37\;9\;\ldots }\;.$

To one of the three authors, the preacher Merkel from Ravensburg, Gotthold Ephraim Lessing dedicated the poem "Auf den Herrn M** den Erfinder der Quadratur des Zirkels".

The circle quadrature of the American physician Edward J. Goodwin even appeared in the first volume of the American Mathematical Monthly in 1894, albeit only as an advertisement by the author. The paper itself is self-contradictory, allowing multiple values for π $\pi$ depending on how you read it. It was the basis for a bill presented to the Indiana legislature in 1897, the so-called Indiana Pi Bill, by which Goodwin's findings were to become law.

Art and culture

As the earliest evidence for the appearance of a so-called "circle squarer" or "quadrator", a passage in Aristophanes' comedy The Birds from the 5th century BC is occasionally cited, in which Meton appears as a surveyor and wants to determine the ground plan of a new city with geometric aids so that "the circle becomes a square". What is meant, however, is not the squaring of a circle, but the laying out of two streets meeting at right angles, even if the expression seems like an allusion to the squaring of a circle.

In 1321, Dante Alighieri, in his work Divine Comedy, presented the squaring of the circle as a task beyond human comprehension, which he compared to his own inability to understand paradise:

"As to measure the circle in vainThe
mathematician labors with thought,
Because he lacks the principle he needs: 135

That's how I felt about this new sight.
I wanted to see, how the picture to the circle
And where it would find its place;

But my wings here were not enough,
Were not my spirit struck by lightning,
Who contemplated the fulfillment of my wish."

- Dante Alighieri, Ludwig Gottfried Blanc (translator): The Divine Comedy - Paradise - Canto 33, lines 133 to 141

In James Joyce's seminal 1922 novel Ulysses, the main character is Leopold Bloom, an advertising agent. In the summer of 1882, he was working hard to solve the problem of squaring the circle in order to obtain what he thought was a large fortune. Towards the end of the novel, in a long dialogue with his father, Rudolf Virág, he sadly and disappointedly had to admit that he had failed.

"VIRAG [...] You carried yourself, after all, with the intention of devoting a full year to the study of the problem of religion, and the summer months of 1882 to squaring the circle and winning that million. Pomegranate! From the sublime to the ridiculous is but a step. Pajamas, we might say? […]

BLOOM I wish it was the end now. Night suit never was. Hence this one. But tomorrow is a new day, will be. Past was, is today. What is now will then be tomorrow, as it was now, past yesterday."

- James Joyce: Ulysses: Novel

Proximity Constructions

Although an exact solution with compass and ruler is not possible, there are approximate constructions for the circle-square that are exact enough for many purposes. Simple methods, already known in antiquity, give an integer ratio of the diameter or radius of the circle to the side or diagonals of the square. Besides the equation of the circle of diameter 9 with the square of the side 8, mentioned in the Papyrus Rhind, that of the circle of diameter 8 with the square of the diagonal 10 was also known. This construction is found on the one hand in the Babylonians and on the other hand in the publications of the Roman surveyor Vitruvius. It yields the value ^31/8 for π $\pi$ . In order to give a convenient drawing method, Albrecht Dürer takes up this construction again in 1525 in his work Vnderweysung der messung mit dem zirckel und richtscheyt. Dürer is aware that this is a purely approximate solution; he explicitly writes that an exact solution has not yet been found:

"It would be necessary to know quadratura circuli, that is, the equality of a circle and a square, that is, that one had as much content as the other. But this has not yet been demonstrated by scholars. Mechanice, which is incidental, so that it is not lacking in the work, or only by a small amount, may this equality be made. Tear a square and divide the local line into ten parts, and then tear a circle whose diameter is to have eight parts, like the quadrature whose 10; as I have torn open below."

- Albrecht Dürer: The measurement with the compass and the rule of law

Kochański construction

→ Main article: Kochański approximate construction

A classical approximation solution for the half circumference of a circle was discovered by the Polish mathematician Adam Adamandy Kochański in 1685. It makes do with only one opening in the compass. The actual construction consists of a rectification of the semicircle. Kochanski constructed approximately from the given radius a straight line of length $r\cdot \pi ,$ i.e. approximately half the circumference of the circle ${\tfrac {U}{2}}.$ Consequently, the rectangle drawn in red in the accompanying drawing has ${\overline {AZ}}\cdot r=r\;\cdot \approx \pi \cdot r$ almost the same area as the circle with The approximate quadrature follows from this elementarily with the help of mathematical laws of the right triangle, described in Quadrature of the Rectangle. Kochański approximates the number of the circle to four decimal places:

$\pi =3{,}141\;592\ldots \approx {\overline {AZ}}=r\cdot {\sqrt {(3-\tan 30^{\circ })^{2}+4\,}}\ \approx \ 3{,}141\;5{\color {red}33}\cdot r$

Examples to illustrate the errors:

For a circle of radius r = 100 m, the error in side length a would be ≈ -1.7 mm.

For a circle of radius r = 1 m, the error of area would be A ≈ -59 mm².

Construction by Jacob de Gelder

In 1849, an elegant and apparently simple construction by Jacob de Gelder (1765-1848) appeared in Grünert's archives. This was 64 years earlier than the publication of the comparable construction by S. A. Ramanujan.

It is based on the approximation

$\pi \approx {\frac {355}{113}}=3{,}141\;592{\color {red}\;9\;\ldots }$

and the division of the value into the two summands

$3+0{,}141\;592{\color {red}\;9\;\ldots }.$

The value of this fraction $\pi$ already has six decimal places in common with the circle number π It originates from the Chinese mathematician Zu Chongzhi from the 5th century and is therefore also called Zu Chongzhi fraction.

Jacob de Gelder did not construct the side of the square; it was enough for him to find the following value:

${\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}=0{,}141\;592{\color {red}\;9\;\ldots }$ .

The adjacent figure - described below - shows Jacob de Gelder's construction with continuation.

Draw two perpendicular centre lines of a circle with radius CD = 1 and determine the intersection points A and B. Set the distance CE = $\tfrac{7}{8}$ and connect E to A. Set the distance AF = ${\tfrac {1}{2}}$ on AE and from A on. Draw FG parallel to CD and connect E to G. Draw FH parallel to EG, then AH = ${\tfrac {4^{2}}{7^{2}+8^{2}}}.$ Determine BJ = CB and then JK = AH. Bisect AK in L and draw the Thales circle around L starting from A, yielding the intersection M. The distance BM is the square root of AK and hence the side length a of the nearly equal area square we are looking for.

Examples to illustrate the errors:

For a circle with radius r = 100 km, the error of the side length a ≈ 7.5 mm would be

For a circle with radius r = 1 m, the error of the area A ≈ 0.3 mm² would be

Construction by E. W. Hobson

A particularly simple and easily comprehensible construction was made by E. W. Hobson in 1913, which requires only three semicircles and two perpendicular lines for the side of the square.

The adjacent picture shows the construction with the circle drawn in and the square we are looking for.

Specifications and Description:

Circle with diameter $AOB$
${\overline {OD}}={\frac {3}{5}}\cdot r,\;{\overline {OF}}={\frac {3}{2}}\cdot r,\;{\overline {OE}}={\frac {1}{2}}\cdot r.$

Draw the semicircles $DGE,AHF$ with ${\overline {DE}}$ and ${\overline {AF}}$ as diameters. Finally, construct the perpendicular to ${\overline {AB}}$ through $O.$ The intersections and thus produced give the side length of the square we are looking for

${\overline {GH}}=r\cdot 1{,}772\;4{\color {red}67\ldots }\;[LE].$

For a circle of radius four decimal places of the side length of the square are equal to those in $r=1\;[LE]$ π ${\sqrt {\pi }}=1{,}772\;453$

Example to illustrate the errors:

For a circle with radius r = 100 m, the error of the side length a ≈ 1.4 mm would be

For a circle of radius r = 1 m, the error of area A would be ≈ 46 mm².

Constructions by S. A. Ramanujan

Also in 1913 a construction of the Indian mathematician Srinivasa Ramanujan appeared which was also based on the approximation

$\pi \approx {\frac {355}{113}}=3{,}141\;592{\color {red}\;9\;\ldots }$

is based. Ramanujan noted regarding the accuracy of his method that with a circular area of 140,000 square miles, the constructed square side deviated from the true value by only about one inch.

Description (Translation):

Let PQR be a circle with center O, of which PR is the diameter. Bisect PO in H, and let T be the point from the trisection of OR near R. Draw TQ perpendicular to PR and set the chord RS = TQ.

Connect P with S and draw OM and TN parallel to RS. Set a chord PK = PM and draw the tangent PL = MN. Connect R with L, R with K and K with L. Section RC = RH. Draw CD parallel to KL, [CD] meets RL in D.

Then the square over RD is approximately equal to the circle PQR.

For $RS^{2}={\frac {5}{36}}d^{2},$

where is the diameter of the circle.

Thus $PS^{2}={\frac {31}{36}}d^{2}.$

But $PL$ and $PK$ are equal to $MN$ and $PM.$

Thus $PK^{2}={\frac {31}{144}}d^{2},$ and $PL^{2}={\frac {31}{324}}d^{2}.$

Hence, $RK^{2}=PR^{2}-PK^{2}={\frac {113}{144}}d^{2},$

and $RL^{2}=PR^{2}+PL^{2}={\frac {355}{324}}d^{2}.$

But ${\frac {RK}{RL}}={\frac {RC}{RD}}={\frac {3}{2}}{\sqrt {\frac {113}{355}}},$

and $RC={\frac {3}{4}}d.$

Therefore $RD={\frac {d}{2}}{\sqrt {\frac {355}{113}}}=r{\sqrt {\pi }},$ almost equal.

Note: If the area of the circle is 140,000 square miles, then RD is about one inch greater than the true length.

In a paper from the following year (1914) Ramanujan provided, among other approximations, another quadrature using a compass and ruler. This has the value

$\pi \approx {\sqrt[{4}]{9^{2}+{\frac {19^{2}}{22}}}}=3{,}141\;592\;65{\color {red}2\;\ldots }$

which approaches π $\pi$ even to eight digits. Ramanujan did not construct the side length of the square he was looking for in this quadrature; it was sufficient for him to represent the distance OS. In the adjacent continuation of the construction, the distance OS is used together with the distance OB to represent the mean proportional (red distance OE).

Description (Translation):

Let AB (Fig. 2.) be a diameter of a circle, the centre of which is O. Bisect the arc ACB in C and third AO in T. Connect B with C and trace on it CM and MN of equal length to AT. Connect A with M and A with N and on the latter trace AP of the same length as AM. Draw PQ parallel to MN, where Q meets AM. Connect O with Q and draw TR parallel to OQ, where R meets AQ. Draw AS perpendicular to AO and equal in length to AR, then connect O with S. Then the mean proportional between OS and OB will be very near one-sixth of the circumference of the circle, the error being less than one-twelfth of an inch when the diameter is 8000 miles long.

Continuation of the construction up to the side length of the square:
Extend AB beyond A and draw the arc b1 around O with radius OS, you get S'. Bisect BS' in D and draw the Thales circle b2 over D. Draw a straight line from O through C to the Thales circle b2, it intersects b2 in E. The distance OE is the above described mean proportional between OS and OB also called geometric mean, it results from the height theorem of Euclid. Extend the distance EO beyond O and transfer EO to it two more times, we get F and _{A1 and} thus the length of the distance EA1 with the approximate value of π described above. $\pi$ , half the circumference of the circle. Bisect the distance EA1 in G and draw the Thales circle b3 over G. Transfer the distance OB from _A1 to the distance EA1, we get H. Erect a perpendicular on EA1 from H to the Thales circle b3, we get _B1. Connect _A1 with _B1, thus the side length is constructed for an almost equal area square _A1B1C1D1.

Examples to illustrate the errors:

For a circle with radius r = 10,000 km, the error of the side length a would be ≈ -2.8 mm

For a circle with radius r = 10 m, the error would be the area A ≈ -0.2 mm².

Construction by Louis Loynes

A simpler method was published by Louis Loynes in 1961, based on the observation that the area of the circumcircle of a right triangle is equal to the square over the larger cathetus if the tangent of the smaller angle, that is, the ratio of the smaller to the larger cathetus,

$\sqrt{\frac{4}{\pi}-1} = 0{,}5227232\dots$

a value that is very close to the fraction

$\frac{23}{44} = 0{,}5227272\dots$

lies. This gives a simple approximation using the (constructible) right triangle with a 23:44 ratio of cathets to square. The approximated value for the circle number of

$\pi \approx {\frac {7744}{2465}}=3{,}141\;5{\color {red}82\;\ldots }$

is slightly better than Kochański's design.

Examples to illustrate the errors:

For a circle of radius r = 1 km, the error in side length a would be ≈ -3 mm.

For a circle of radius r = 1 m, the error of area would be A ≈ -11 mm².

Approximate solution using a constructed fraction

If a fraction whose value approximately corresponds to $\pi$ the circle number π constructed on a ray using the third ray theorem, it is possible with more or less constructive effort to $\pi$ represent any desired number of decimal places of π To find the side length of the square, for example, the fraction

${\frac {245850922}{78256779}}=3{,}141\;592\;653\;589\;793{\color {red}\;160\;\ldots }$

can be used. As an approximate value of the circular number π $\pi$ it yields a remarkable fifteen equal decimal places. The reciprocal fraction of this fraction originates from Johann Heinrich Lambert, who published it in his book Beyträge zum Gebrauche der Mathematik und deren Anwendung already in 1770.

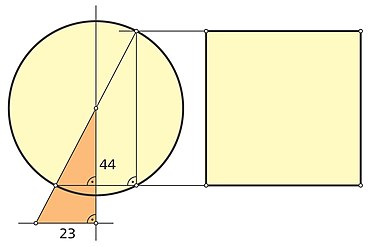
Loynes' Construction (1961).

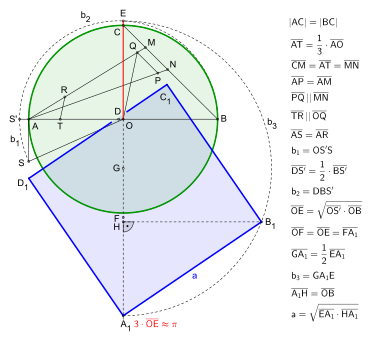
Approximate construction according to S. A. Ramanujan (1914) with continuation of the construction (dashed lines), see the animation.

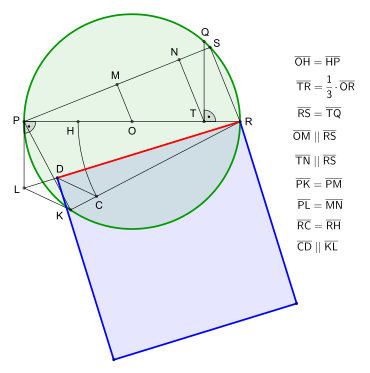
Approximation construction according to S. A. Ramanujan (1913) with drawn square

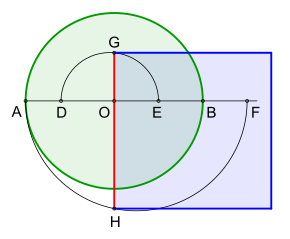
Approximate construction according to E. W. Hobson, with continuation of the construction.

Babylonian procedure after Dürer (1525)

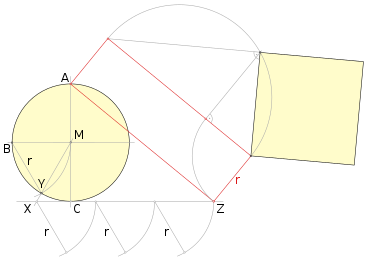
Approximate construction of Kochański (1685).

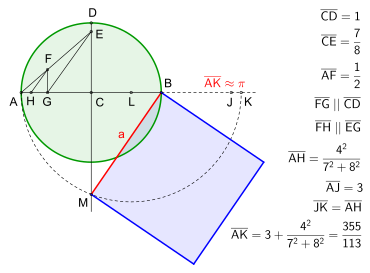
Construction by Jacob de Gelder with continuation (dashed lines).

Squaring the circle

Popularity of the circle quadrature

Prominent circle squares

Art and culture

Proximity Constructions

Kochański construction

Construction by Jacob de Gelder

Construction by E. W. Hobson

Constructions by S. A. Ramanujan

Construction by Louis Loynes

Approximate solution using a constructed fraction

Search by letter