Speed of light

The speed of light ( after lat. celeritas: speed) is usually understood as the speed of propagation of light in vacuum. Besides light, all other electromagnetic waves as well as gravitational waves propagate with this speed. It is a fundamental natural constant, whose meaning in the special and general relativity theory goes far beyond the description of the electromagnetic wave propagation.

The unit of length meter is defined by the speed of light in vacuum. The speed of light was set to exactly 299792458 m/s for this purpose.

In a material medium like air or glass, the propagation speed of light is smaller. If it is not obvious from the context, it is made clear by word additions whether the speed of light in vacuum or in the material is meant. In both cases one uses the formula sign ; occasionally the index zero is used for the speed of light in vacuum ( $c_{0}$ ).

According to Maxwell's equations of electrodynamics, the speed of light does not depend on the speed of the light source. From this statement together with the principle of relativity it follows that the speed of light also does not depend on the state of motion of the receiver used for its measurement. From this, Albert Einstein developed the theory of relativity. It states, among other things, that the vacuum speed of light an insurmountable speed limit for the motion of mass and for the transmission of energy and information in the universe. Particles without mass, like photons, always move with this limit speed, all particles with mass always move slower. As a consequence of special relativity (SRT), the natural constant the previously independent concepts of energy and mass in the equivalence of mass and energy $E=mc^{2}$ . Place and time are combined by to space-time and described by the four-vector (ct,x,y,z) in a four-dimensional space.

Value

The value of the speed of light in vacuum is

$c=299\,792\,458\ {\frac {\text{m}}{\text{s}}},$

thus approx. 300000 km/s or 1.08 billion km/h. This value is valid exactly because the unit of measurement "meter" is implicitly defined since 1983 by assigning this value to the speed of light.

Previously, the meter had been defined as a multiple of the wavelength of a certain atomic transition, and the speed of light was a quantity to be determined experimentally. However, with the progress in measurement technology, the speed of light could be determined more precisely than this wavelength and thus the meter itself. Therefore, the new definition of the meter was decided in 1983.

Time-true representation of a beam of light traveling from the earth to the moon; duration: about 1.3 seconds

Natural units

Many representations of relativistic physics give lengths by light travel times or vice versa times by the length of the way which light passes during this time. A light year is then called shorter a year. In these units (see Planck units) is valid

$1{\text{ Lichtsekunde}}=299\,792\,458{\text{ Meter}}$

and light has the dimensionless speed of one second per second

c=1 .

The formula picture of physical relations is simplified by this choice of units, for example the relation of energy and momentum ${\vec {p}}$ a particle of mass then no longer $E^{2}=m^{2}c^{4}+{\vec {p}}^{\,2}c^{2}$ , but $E^{2}=m^{2}+{\vec {p}}^{\,2}$ .

If you want to recover the equation in the International System of Units (SI) from an equation in natural units, you must multiply each summand by so many factors that both sides of the equation and each summand have equal SI units. For example, in SI, energy has the unit of measurement of a mass times the square of a velocity, and an impulse has the unit of measurement of a mass times a velocity. Therefore, in order for the formula $E^{2}=m^{2}+{\vec {p}}^{\,2}$ to have quantities of the same unit of measure, energy times energy, on the right-hand side in SI as on the left-hand side, the mass square must be multiplied by $c^{4}$ and the momentum square must be $c^{2}$ multiplied by Thus, the equation valid in SI is obtained $E^{2}=m^{2}\,c^{4}+{\vec {p}}^{\,2}\,c^{2}.$

Technical meaning

Information in telecommunications systems propagates at 70 percent (optical fibers) to 100 percent (vacuum, outer space, practically also air) of the speed of light. This results in delay times that cannot be avoided. Along the earth's surface, the maximum distance between two locations is about 20,000 km. This would correspond to 67 ms transit time at vacuum light speed. The actual transmission time is always longer. In the case of atmospheric transmission, the wave is reflected in the various layers of the atmosphere and on the earth's surface and thus has a longer distance to travel.

Microprocessors today operate at clock frequencies in the order of 1 to 4 GHz. During one clock cycle, electrical signals in circuits with low-k dielectrics travel between 5 and 20 cm. When designing circuits, these travel times are not negligible.

Geostationary satellites are located 35,786 km above the equator. To receive a response to telephone or television signals on this path, the signal must have traveled at least 144,000 km: from the transmitter to the satellite, then to the receiver, then back the same way. This transit time is about 480 ms.

Space probes are often many millions or billions of kilometers from Earth at their destinations. Even at the speed of light, radio signals travel several minutes to hours to reach them. The response back to Earth takes the same amount of time again. Extraterrestrial vehicles such as the Mars rover Opportunity must therefore be able to steer themselves and detect hazards, because the ground station can only react to incidents minutes later.

Speed of light and electrodynamics

It follows from Maxwell's equations that electric and magnetic fields can oscillate, transporting energy through empty space. Thereby the fields obey a wave equation, similar to the one for mechanical waves and for water waves. The electromagnetic waves transfer energy and information, which is used in technical applications for radio, radar or laser.

Plane wave or spherical wave in vacuum

According to Maxwell's equations, the velocity of plane or spherical electromagnetic waves in vacuum is the inverse of the square root of the product of the electric field constant ε $\varepsilon _{0}$ and the magnetic field constant μ $\mu _{0}\colon$

$c={\frac {1}{\sqrt {\varepsilon _{0}\,\mu _{0}}}}$

From this, Maxwell calculated in 1865, using the then known values for ε $\varepsilon _{0}$ and μ $\mu _{0}$ value of $310\,740\;{\text{km/s}}$ and concluded:

"This speed is so close to the speed of light that we have a strong reason to believe that light itself (including thermal radiation and other radiation, if any), is an electromagnetic wave."

Maxwell's assumption has been confirmed in all observations of electromagnetic radiation.

Plane wave or spherical wave in a medium

In a medium, the two field constants are modified by the material, which is $\mu _{\mathrm {r} }$ accounted for by the factors relative permittivity ε $\varepsilon _{\mathrm {r} }$ and relative permeability μ Both depend on the frequency. Accordingly, the speed of light in the medium is

$c_{\text{medium}}={\frac {1}{\sqrt {\varepsilon \,\mu }}}={\frac {1}{\sqrt {\varepsilon _{0}\,\varepsilon _{\mathrm {r} }\,\mu _{0}\,\mu _{\mathrm {r} }}}}={\frac {c}{\sqrt {\varepsilon _{\mathrm {r} }\,\mu _{\mathrm {r} }}}}$ .

The ratio of the speed of light in vacuum to that in a medium is the (frequency-dependent) refractive index the medium. The relation of the refractive index with the relative permittivity and the relative permeability is also called maxwell's relation:

$n={\frac {c}{c_{\text{medium}}}}={\sqrt {\varepsilon _{\mathrm {r} }\,\mu _{\mathrm {r} }}}$

Because of the generally given dependence of ε $\varepsilon _{\mathrm {r} }$ and μ $\mu _{\mathrm {r} }$ on the frequency of the wave, note that $c_{\mathrm {medium} }$ denotes the phase velocity in the medium at which points of the same phase (e.g., minima or maxima) of a plane wave progress at constant amplitude. e.g. minima or maxima) of a plane wave progress with constant amplitude. The envelope of a spatially confined wave packet, on the other hand, propagates at the group velocity. In media, these two velocities differ more or less from each other. In particular, a refractive index simply n<1 means that wave crests faster than c {\displaystyle . Wave packets transporting information and energy are still slower than .

Transverse modulated wave in vacuum

According to Maxwell's equations, the speed of light $c=1/{\sqrt {\varepsilon _{0}\,\mu _{0}}}$ etc., which is independent of the wavelength, results for the case of an infinitely extended plane wave in vacuum with a well-defined direction of propagation. In contrast, every practically realizable light wave always has a certain beam profile. If this is represented as a superposition of plane waves with slightly different directions of propagation, the individual plane waves all have the vacuum light velocity but this is not necessarily true for the wave resulting from the superposition. A slightly slowed down wave results. This could be proved at special formed Bessel beams of microwaves and visible light, even for the velocity of single photons. However, this effect is negligibly small for all practically realizable light waves, even for sharply focused laser beams.

The red point moves with the (average) phase velocity, the green points with the group velocity

Speed of light in matter

In matter, light is slower than in vacuum, and there, as derived above, $c_{\,\mathrm {Medium} }={c}/{n}$ with a refractive index , which is greater than 1.

In air near the ground, the speed of light is about 0.28 ‰ lower than in vacuum (i.e., about 299,710 km/s), in water it is about 225,000 km/s (- 25%), and in glasses with high refractive index it is as low as 160,000 km/s (- 47%).

In some media, such as Bose-Einstein condensates or photonic crystals, there is a very large dispersion for certain wavelengths. Light propagates in them at a significantly slower rate. In 1999, for example, the research group of the Danish physicist Lene Hau was able to bring light to a group velocity of about 17 m/s. This was the first time that light was propagated at a group velocity.

If two transparent media are adjacent to each other, the different speed of light in the two media causes refraction of the light at the interface. Since the speed of light in the medium also depends on the wavelength of the light, light of different colors is refracted differently, and white light splits into its different color components. This effect can be observed directly, for example, with the aid of a prism.

In a medium, particles can be faster than light in the same medium. If they are electrically charged, such as electrons or protons, the Cherenkov effect occurs: The particles radiate light, just as a supersonic airplane drags the sonic boom behind it. This can be observed, for example, in swimming pool reactors. In them, there is water between the fuel elements. The beta radiation of the fission products consists of electrons that are faster than the speed of light in water. The Cherenkov light they emit makes the water glow blue.

The Cherenkov effect is used in particle detectors to detect fast charged particles.

Cherenkov light of a Triga reactor

Speed of light and particle physics

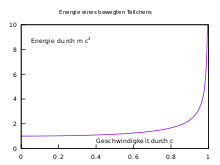
Particles without mass move always and in every inertial frame with speed of light. The best known massless particle showing this property is the photon. It mediates the electromagnetic interaction that governs much of the physics of everyday life. Other massless particles in the Standard Model of particle physics are the gluons, the mediating particles of the strong interaction. Particles with non-zero mass are always slower than light. When accelerated, their energy increases E(v) because of the relativistic energy-momentum relation according to

$E(v)={\frac {m\,c^{2}}{\sqrt {1-{v}^{2}/c^{2}}}}.$

Here is the velocity of the particle with respect to the inertial frame chosen to describe the process. The closer the magnitude of the particle velocity the speed of light the more the quotient $v^{2}/c^{2}$ 1, and the smaller the root in the denominator becomes. The more the particle velocity approaches the velocity of light, the larger the energy required for it. So with finitely high energy you can accelerate a particle arbitrarily close to the speed of light, but you cannot reach it.

The relationship between energy and velocity predicted by relativity has been proven in various experiments.

Among other things, it has implications for the technology of particle accelerators. The orbital period of a packet of electrons orbiting in a synchrotron, for example, hardly changes with further acceleration; the synchronization of the individual accelerating alternating fields can therefore be constant. In contrast, it must be continuously adapted to the increasing velocity in the case of heavier particles which are fed at lower velocities.

The vacuum light velocity as limit velocity of massive particles: If their velocity goes towards the speed of light, the energy, i.e. E(v) , over all limits.

Superluminal velocity

→ Main article: Superluminal velocity

There is speculation about particles moving faster than the speed of light. One example are hypothetical particles called tachyons. According to relativity, tachyons could not interact with normal matter: otherwise, it would not be possible to distinguish between cause and effect, equally for all observers. The theoretical foundations of the tachyon concept are controversial. An experimental proof of tachyons did not succeed so far.

Furthermore, in recent years, publications claiming the observation of faster-than-light speeds have caused a particular stir. But either it could be shown that the apparently faster-than-light signal transmission resulted from a misinterpretation of the data (faster-than-light jets, superluminal tunneling), or the measurements could not be reproduced and eventually turned out to be erroneous (see, for example, measurements of neutrino velocity).

Historical background

Speculations about finiteness

Historically assumed height of the speed of light
Year (approx.)	Researchers	Speed of light
450 BC	Empedocles	finally
350 BC	Aristotle	infinite
100	Heron of Alexandria	infinite
1000	Avicenna/Alhazen	finally
1350	Sayana	finally
1600	Johannes Kepler	infinite
1620	René Descartes	infinite
1620	Galileo Galilei	finally

The question of whether light propagates infinitely fast or whether it has a finite speed was already of interest in the philosophy of antiquity. Light covers a kilometer in only three microseconds. With the observation possibilities of the antiquity a ray of light is thus inevitably apparently in the moment of its origin at the same time already at its goal.

Nevertheless, Empedocles (around 450 BC) already believed that light is something that is in motion and therefore needs time to cover distances. Aristotle, on the other hand, thought that light came from the mere presence of objects, but was not in motion. He argued that otherwise the speed would have to be so enormous as to be beyond human imagination. Because of his reputation and influence, Aristotle's theory found general acceptance.

An ancient theory of vision assumed that the light needed for seeing was emitted by the eye. An object should therefore be seen when the light rays from the eye hit it. Building on this idea, Heron of Alexandria also endorsed the Aristotelian theory. He argued that the speed of light must be infinite, since even the most distant stars can be seen as soon as one opens one's eyes.

In the oriental world, on the other hand, the idea of a finite speed of light was also widespread. In particular, the Persian philosophers and scientists Avicenna and Alhazen (both around the year 1000) believed that light has a finite speed. However, their supporters were in the minority compared to the followers of the Aristotelian theory.

At the beginning of the 17th century, the astronomer Johannes Kepler believed that the speed of light was infinite, at least in a vacuum, because empty space was no obstacle for light. Here already the idea appears that the speed of a light ray could be dependent on the traversed medium.

Francis Bacon argued that light need not necessarily be infinitely fast, but perhaps only faster than perceptible.

René Descartes assumed an infinite speed of light. Sun, moon and earth lie in a line during a solar eclipse. Descartes argued that these celestial bodies would seem to be out of alignment for an observer at that time if the speed of light was finite. Since such an effect was never observed, he saw his assumption confirmed. Descartes believed so strongly in an infinite speed of light that he was convinced his world view would collapse if it were finite.

This is contrasted by the theories of Isaac Newton and Christiaan Huygens around the year 1700 with finite speed of light. Newton saw light as a stream of particles, while Huygens interpreted light as a wave. Both could explain the law of refraction by assuming the speed of light to be proportional (Newton) or inversely proportional (Huygens) to the refractive index. Newton's idea was considered to be disproved since interference and diffraction could be observed in the 19th century and the velocity could be measured in media.

Since there was the first measurement of the speed of light at Huygens' time, which in his opinion was much too high for bodies with mass to reach it, he proposed with the aether an elastic (neither visible nor measurable) background medium, which allowed the propagation of waves, similar to sound in the air.

Measurement of the speed of light

Around 1600, Galileo Galilei was the first to attempt to measure the speed of light using scientific methods by placing himself and an assistant, each with a signal lantern, on two hills of known distance. The assistant was to return Galileo's signal immediately. He had already successfully determined the speed of sound using a comparable method. To his astonishment, no repeatable measurable time remained after deduction of the reaction time of the assistant. This did not change even when the distance was increased to the maximum possible visibility of the lanterns. Isaac Beeckman proposed a modified version of the experiment in 1629, in which the light was to be reflected by a mirror. Descartes criticized such experiments as superfluous, since more accurate observations had already been made using solar eclipses and had yielded a negative result. Nevertheless, the Accademia del Cimento repeated the experiment in Florence in 1667. Here the lamps were about a mile apart. Again, no delay could be observed. This confirmed Descartes in his assumption of an infinitely fast propagation of light. Galileo and Robert Hooke, on the other hand, interpreted the result to mean that the speed of light was so high that it could not be determined by this experiment.

The first proof that the speed of light is finite was made by the Danish astronomer Ole Rømer in 1676. He found seasonally varying transit times for clock signals from Jupiter (entry of Jupiter's moon Io into Jupiter's shadow), while on this side the Earth's rotation served as a stable time reference. He gave a transit time of light of 22 min for the Earth's orbit diameter. The correct value is shorter (16 min 38 s). Since Rømer did not know the diameter of the Earth's orbit, he did not give a value for the speed of light. This was done two years later by Christiaan Huygens. He related the running time value of Rømer to the diameter of the earth's orbit around the sun, which was by chance almost correctly given by Cassini in 1673 (see solar parallax for the gradual improvement of this value) and came to a speed of light of $213\,000\;{\text{km/s}}$ .

James Bradley found another astronomical method in 1728 by determining the variations of the star positions by an angle of 20″ during the orbit of the Earth around the Sun (aberration). His measurements were an attempt to observe the parallax of fixed stars in order to determine their distances. From this, Bradley calculated that the light is $10\,210$ times faster than the Earth during its orbit (measurement error 2%). His measurement (published in 1729) was considered at the time as further proof of a finite speed of light and - at the same time - of the Copernican world system. However, for the calculation of the speed of light, he also needed the Earth's orbital radius.

The first terrestrial determination of the speed of light was achieved by Armand Fizeau with the gear wheel method. In 1849, he sent light through a rotating gear wheel onto a mirror several kilometers away, which reflected it back through the gear wheel. Depending on how fast the gear wheel is rotating, the reflected light that passed through a gap in the gear wheel on the way there either falls on a tooth or passes through a gap again, and only then can it be seen. At that time, Fizeau arrived at a value that was too large by 5%.

Léon Foucault further improved the method in 1850 by using the rotating mirror method to significantly shorten the measurement distances. This enabled him to prove the material dependence of the speed of light for the first time: Light propagates more slowly in other media than in air. In the experiment, light falls on a rotating mirror. From this, it is deflected onto a fixed mirror, where it is reflected back onto the rotating mirror. However, since the rotating mirror has continued to rotate in the meantime, the light beam is now no longer reflected back to the starting point. By measuring the displacement of the point, it is possible to determine the speed of light given a known rotational frequency and distances. Foucault published his result in 1862 and gave as $298\,000$ kilometers per second.

Simon Newcomb and Albert A. Michelson again built on Foucault's apparatus and improved the principle again. In 1926, Michelson also used rotating prism mirrors in California to send a beam of light from Mount Wilson to Mount San Antonio and back. He obtained $299\,796\;{\text{km/s}}$ , only 12 ppm above today's value.

Historical values for the speed of light
Year	Researchers	Method	Speed of light in km/s
about 1620	Galileo Galilei	Time delay of observation of lanterns covered by hand	At least several km/s
1676/78	Ole Rømer / Christiaan Huygens	Time delay in astronomical observations	$213\,000$
1728	James Bradley	Aberration	$301\,000$
about 1775	?	Venus transit 1769	$285\,000$
1834	Charles Wheatstone	Rotating mirror method for measuring the speed of electric current	$402\,336$
1849	Armand Fizeau	Gear method	$315\,000$
1851	Léon Foucault	Rotating mirror method	$298\,000\pm 500$
1865	James Clerk Maxwell	Maxwell equations	$310\,740$
1875	Alfred Cornu	Rotating mirror method	$299\,990$
1879	Albert A. Michelson	Rotating mirror method	$299\,910\pm 50$
1888	Heinrich Hertz	Frequency and wavelength measurement of standing radio waves	$300\,000$
1926	Albert A. Michelson	Rotating mirror method	$299\,796\pm 4$
1947	Louis Essen, Albert Gordon-Smith	Electrical cavity resonator	$299\,792\pm 3$
1958	Keith Froome	Interferometer	$299\,792{,}5\pm 0{,}1$
1973	Boulder group at NBS	Laser measurement	$299\,792{,}4574\pm 0{,}001$
1983	Definition of CGPM	Determination of the speed of light by redefinition of the meter	$299\,792{,}458$

On the constancy of the speed of light

First considerations

With his investigations on aberration of 1728, James Bradley was not only able to determine the speed of light itself, but also to make statements about its constancy for the first time. He observed that the aberration varies identically for all stars in the same viewing direction during one year. From this, he concluded that the speed at which starlight arrives on Earth is the same for all stars within the limits of his measurement accuracy of about one percent.

However, to clarify whether this speed of arrival depends on whether the Earth is moving toward or away from a star on its way around the Sun, this measurement accuracy was not sufficient. This question was first investigated by François Arago in 1810 by measuring the deflection angle of starlight in a glass prism. According to the then accepted corpuscular theory of light, he expected a change in this angle of a measurable order of magnitude, since the speed of the incident starlight should add to the speed of the Earth on its path around the Sun. However, there were no measurable variations in the deflection angle over the course of the year. Arago explained this result with the thesis that starlight is a mixture of different velocities, while the human eye can perceive from it only one. From today's point of view, however, his measurement can be regarded as the first experimental proof of the constancy of the speed of light.

With the advent of the concept of light as a wave phenomenon, Augustin Fresnel formulated a different interpretation of the Arago experiment in 1818. According to this, the analogy between mechanical waves and light waves included the idea that light waves must propagate in a certain medium, the so-called aether, just as water waves propagate in water. The aether was supposed to be the reference point for a preferred inertial frame of reference. Fresnel explained the result of Arago by the assumption that this aether is partly carried along inside matter, in this case in the used prism. Thereby, the degree of entrainment would suitably depend on the refractive index.

Michelson-Morley experiment

→ Main article: Michelson-Morley experiment and history of special relativity.

In 1887, Albert A. Michelson and Edward W. Morley performed a significant experiment to determine the velocity of the Earth relative to this assumed aether. For this purpose, the dependence of the light travel times on the state of motion of the aether was investigated. The experiment resulted contrary to expectation always the same running times. Also repetitions of the experiment to different phases of the earth orbit around the sun always led to the same result. An explanation on the basis of a far-reaching ether guidance by the earth as a whole failed because in this case there would be no aberration at stars perpendicular to the direction of motion of the earth.

A solution compatible with Maxwellian electrodynamics was achieved with the length contraction proposed by George FitzGerald and Hendrik Lorentz. Lorentz and Henri Poincaré further developed this hypothesis by introducing time dilation, but combining this with the assumption of a hypothetical ether whose state of motion would have been impossible to determine in principle. This means that in this theory the speed of light is "real" constant only in the ether system, independent of the motion of the source and the observer. This means, among other things, that maxwell's equations should take the usual form only in the ether system. However, this was taken into account by Lorentz and Poincaré by introducing the Lorentz transformation in such a way that the "apparent" speed of light is also constant in all other reference systems and thus everyone can claim to be at rest in the ether. (The Lorentz transformation was thus interpreted only as a mathematical construction, while Einstein (1905) was to revolutionize all previous ideas about the structure of space-time on its basis, see below). Poincaré still stated in 1904 that the main feature of the Lorentzian theory was the unpassability of the speed of light for all observers, independent of their state of motion relative to the aether (see Lorentzian aether theory). That means, also for Poincaré the aether existed.

However, a theory in which the ether system was assumed to exist but remained undetectable was very unsatisfactory. A solution of the dilemma was found by Einstein (1905) with the special relativity theory by giving up the conventional ideas of space and time and replacing them by the principle of relativity and the light constancy as starting points or postulates of his theory. This solution was formally identical with the theory of H. A. Lorentz, however, as with an emission theory, it got along completely without "ether". He took the light constancy from the Lorentzian aether, as he explained in 1910. In contrast to Poincaré and Lorentz, he explained that just because of the equality of the reference frames and thus the undetectability of the aether, the concept of aether is meaningless at all. In 1912 he summarized this like this:

"It is generally known that on the principle of relativity alone a theory of the transformation laws of space and time cannot be founded. It is well known that this is connected with the relativity of the concepts 'simultaneity' and 'shape of moving bodies'. To fill this gap, I introduced the principle of constancy of light velocity borrowed from H. A. Lorentz's theory of the light ether at rest, which, like the principle of relativity, contains a physical presupposition which seemed to be justified only by the relevant experiences (experiments of Fizeau, Rowland, etc.)."

Thus, the independence of the speed of light from the speed of the uniformly moving observer is the basis of the theory of relativity. This theory is generally accepted since decades due to many very exact experiments.

Independence from the source

→ Main article: Emission theory

With the Michelson-Morley experiment the constancy of the speed of light was confirmed for an observer moving with the light source, but not at all for an observer not moving with the source. Because the experiment can also be explained with an emission theory, according to which the speed of light in all reference systems is only constant relative to the emission source (that is, in systems where the source moves with ±v, the light would consequently propagate with c ± v). Albert Einstein also briefly considered such a hypothesis before 1905, which was also the reason that he always used the MM experiment in his writings as a confirmation of the principle of relativity, but not as a confirmation of the constancy of light.

However, an emission theory would require a complete reformulation of electrodynamics, which was opposed by the great success of Maxwell's theory. The emission theory was also experimentally refuted. For example, the orbits of double stars observed from Earth would have to be distorted at different speeds of light, but this has not been observed. In the decay of π0-mesons moving at approximately the resulting photons should have taken on the velocity of the mesons and moved at approximately twice the speed of light, but this was not the case. The Sagnac effect also demonstrates the independence of the speed of light from the motion of the source. All these experiments find their explanation in the special relativity theory which states among other things: Light does not overtake light.

Variable speed of light and constancy in the observable universe

Although the constancy of the speed of light has been experimentally demonstrated, there is as yet no sufficiently convincing explanation for its constancy and its particular value. Loop quantum gravity, for example, dictates that the speed of a photon cannot be defined as a constant, but that its value depends on the photon frequency. In fact, there are theories that the speed of light changes with the age of the universe and that it was not constant in the early universe. Albrecht and Magueijo show that the cosmological evolution equations, together with a variable speed of light, can solve the problems of the horizon, flatness, and the cosmological constant. The assumption of a spacetime with three space and two time dimensions gives a natural explanation for the constancy of the speed of light in the observable universe and also for the fact that the speed of light varied in the early universe.

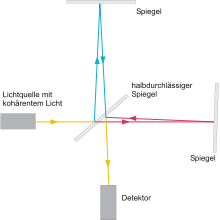
Schematic structure of the Michelson-Morley experiment

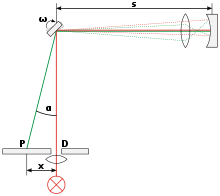
Experimental setup of the experiment of Foucault

Experimental setup of Fizeau's experiment

Questions and Answers

Q: What is the speed of light?

A: The speed of light, denoted by 'c', is a physical constant that is exactly 299,792,458 metres per second (983,571,056 feet per second).

Q: How is the speed of light represented?

A: The speed of light is usually denoted by 'c' and in vacuum medium it is specifically denoted as 'c^0'.

Q: What particles travel at the speed of light?

A: Photons (particles of light) travel at this speed in a vacuum. Additionally, all massless particles such as photons and associated fields—including electromagnetic radiation such as light—travel at c regardless of their source or an observer's inertial frame of reference.

Q: What does special relativity state about the speed of light?

A: According to special relativity, c is the maximum speed at which all energy, matter and physical information can travel in the universe. It also states that the measured speed of light in a vacuum will remain unchanged regardless if either its source or observer are moving relative to each other.

Q: How does c interrelate space and time?

A: In the theory of relativity, c interrelates space and time by appearing in Einstein's famous equation E = mc2. This equation shows how energy can be converted into mass and vice versa.

Q: Is there any evidence that supports special relativity's prediction on the measured speed of light?

A: Yes - so far observations have upheld this prediction that no matter what reference frame it is observed from or what its source may be travelling at -the measured speed remains constant.