Skew lines

In geometry, two straight lines are called skew if they neither intersect nor are parallel to each other. This is not possible in two-dimensional space, since here all conceivable straight lines lie in the same plane and intersect or are parallel. Therefore, wind-skewed straight lines exist only in at least three-dimensional spaces.

The word "skew" comes from the idea that two originally parallel straight lines have been "twisted" around their connecting axis (transversal).

To prove that two straight lines and are skewed, it suffices to show that a direction vector from , a direction vector of and a displacement vector from a point on to a point on are linearly independent. Equivalently, one can show that there is no plane containing both straight lines.

Representation of two skew lines

Spatial image of two skewed straight lines with common plumb line

Calculation of the distance between two skew lines

The uniquely determined path of smallest length connecting two skew lines and called the common perpendicular of the two lines. The line on which the common perpendicular lies is called the minimum transversal of the two lines. This is the uniquely determined straight line which is at right angles to the two straight lines. The length of the common perpendicular of and is the distance d = d(g,h) of the two straight lines.

Given the skew lines and with the supporting points and resp. the support vectors $\vec a = \overrightarrow{OA},\;\vec b = \overrightarrow{OB}$ and the direction vectors ${\vec {v}}$ and ${\vec {w}}$ . Then the parameter forms of the linear equations are

$g\colon {\vec {x}}={\vec {a}}+r{\vec {v}}$

$h\colon {\vec {x}}={\vec {b}}+s{\vec {w}}\ \ \,r,s\in \mathbb {R}$ ,

Where $\vec a,\,\vec b,\,\vec v,\,\vec w \in \R^3$ holds and the three vectors $\vec a - \vec b,\,\vec v,\,\vec w$ must be linearly independent.

The normal vector ${\vec {n}}$ which is perpendicular to the two direction ${\vec {v}}$ and can be ${\vec {w}}$ calculated via the cross product:

$\vec n = \vec v \times \vec w$ and bring to length 1: $\vec n_0 = \frac{\vec v \times \vec w}{|\vec v \times \vec w|}$ .

The calculation of the distance is possible by the orthogonal projection of the connection vector of the support points on the normal vector. To do this, the normal vector is brought to the length 1. The distance of the two skew lines is then

$d(g,h)=|({\vec {a}}-{\vec {b}})\cdot {\vec {n}}_{0}|$ .

Notation with determinants

The two straight line equations are written out as follows

$g\colon {\vec {x}}=\left({\begin{smallmatrix}a_{1}\\[0.7ex]a_{2}\\[0.7ex]a_{3}\end{smallmatrix}}\right)+r\left({\begin{smallmatrix}v_{1}\\[0.7ex]v_{2}\\[0.7ex]v_{3}\end{smallmatrix}}\right)$

$h\colon {\vec {x}}=\left({\begin{smallmatrix}b_{1}\\[0.7ex]b_{2}\\[0.7ex]b_{3}\end{smallmatrix}}\right)+s\left({\begin{smallmatrix}w_{1}\\[0.7ex]w_{2}\\[0.7ex]w_{3}\end{smallmatrix}}\right)\ \ \,r,s\in \mathbb {R}$ .

The distance between the two skew lines using the determinant det is then

$d(g,h)={\frac {\left|\det {\begin{pmatrix}a_{1}-b_{1}&a_{2}-b_{2}&a_{3}-b_{3}\\v_{1}&v_{2}&v_{3}\\w_{1}&w_{2}&w_{3}\end{pmatrix}}\right|}{\sqrt {{\begin{vmatrix}v_{2}&v_{3}\\w_{2}&w_{3}\end{vmatrix}}^{2}+{\begin{vmatrix}v_{3}&v_{1}\\w_{3}&w_{1}\end{vmatrix}}^{2}+{\begin{vmatrix}v_{1}&v_{2}\\w_{1}&w_{2}\end{vmatrix}}^{2}}}}$ .

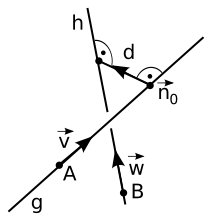
Distance d between two skew lines

Determination of the perpendicular points

The perpendicular foot point $F_{h}$ is obtained by setting up an auxiliary plane point lies on the auxiliary plane, ${\vec {v}}$ and ${\vec {n}}$ span the auxiliary plane.

$E\colon {\vec {x}}={\vec {a}}+r{\vec {v}}+t{\vec {n}}\ \ ,r,t\in \mathbb {R}$ ,

where the normal vector is determined by

$\vec n = \vec v \times \vec w$ .

The intersection of and gives the plumb bob $F_{h}$ :

$\vec F_h=\frac{ \vec a \cdot \vec n_1 - \vec b \cdot \vec n_1 }{ \vec w \cdot \vec n_1 } \vec w + \vec b$ where $\vec n_1 = \vec v \times (\vec v \times \vec w)$

Similarly, we obtain F_g with the plane $E'\colon {\vec {x}}={\vec {b}}+s{\vec {w}}+t{\vec {n}}\ \ \,s,t\in \mathbb {R}$ and its intersection with :

$\vec F_g=\frac{ \vec b \cdot \vec n_2 - \vec a \cdot \vec n_2 }{ \vec v \cdot \vec n_2 } \vec v + \vec a$ where $\vec n_2 = \vec w \times (\vec v \times \vec w)$

With this method, the distance not need to be calculated.

The perpendicular foot points can also be determined by setting the two (for the time being unknown) points:

${\vec {F}}_{h}={\vec {a}}+r{\vec {v}}$ and ${\vec {F}}_{g}={\vec {b}}+s{\vec {w}}$

and then move one along ${\vec {n}}$ and make it coincide with the other:

${\vec {a}}+r{\vec {v}}+u{\vec {n}}={\vec {b}}+s{\vec {w}}$ .

A line-by-line resolution yields a system with three variables: , and . The footers are then:

${\vec {a}}+r{\vec {v}}$ and ${\vec {b}}+s{\vec {w}}$ .

The distance given by $|u{\vec {n}}|$

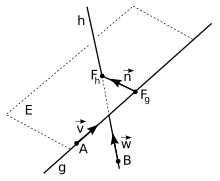
Drawing for determining the perpendicular foot points

Skew lines

Calculation of the distance between two skew lines

Notation with determinants

Determination of the perpendicular points

Search by letter