Sidereal time

Sidereal time is a time scale used in astronomy and is based on the apparent motion of the stars due to the rotation of the Earth. A sidereal day is the length of time it takes for the starry sky (more precisely, the vernal equinox) to make one complete apparent revolution around the Earth. Compared to the commonly used solar time, which is based on the apparent orbit of the Earth by the Sun, the sidereal day is just under four minutes shorter than the solar day.

Like the solar day, the sidereal day is also divided into 24, but shorter hours. It begins when the vernal equinox passes the meridian of the observing site and ends there at its next passage. The observer - usually an astronomer in an observatory - infers the current celestial aspect from the sidereal time. Sidereal time is derived from the right ascension angle - a primary measure of the position of stars in the sky. A star with, for example, 15° difference in right ascension to the vernal equinox passes the meridian one sidereal hour later than the latter. This fact can be briefly stated by saying that it is, for example, 1:00 sidereal time. It should be noted, however, that sidereal time is a time bound to location. To facilitate time comparison for observations made at different locations, local sidereal clocks are set to Greenwich sidereal time. The time difference is - the same as for solar time - 1 hour for 15° difference in longitude between the observation locations.

Observation work using sidereal time has the advantage that at the same sidereal time the stars are always in the same direction in the sky. Compared to the ordinary clock, the sidereal time clock is about 4 more minutes ahead every day. After one year it overtakes the latter and coincides with it again for a short time.

The general determination of time according to Universal Time (UT) (a solar time) is made in practice by the more exact possible observation of the star positions. The sidereal time determined in this way is converted into the corresponding UT using a formula established by convention (see below).

Definition and properties

The sidereal time is defined as the hour angle of the vernal equinox. If you refer to the mean vernal equinox, you get the mean sidereal time. If you refer to the true vernal equinox, you get the apparent or true sidereal time.

The cause for the continuous increase of the mentioned hour angle is the earth rotation. The sidereal time is subject to all short- and long-term irregularities of the earth's rotation and is therefore not a uniformly proceeding measure of time. However, it is always a faithful reflection of the angle of rotation of the Earth with respect to the vernal equinox.

Since the vernal equinox moves relative to the fixed star background due to precession, a sidereal day (i.e., one full revolution of the Earth relative to the vernal equinox) is slightly shorter than a rotation of the Earth (i.e., one full revolution of the Earth relative to the fixed star background). Since the vernal equinox moves backwards along the ecliptic by about 0.137 arc seconds per day, a mean sidereal day is 0.009 seconds shorter than a rotation of the Earth.

The true vernal equinox differs from the mean vernal equinox by its variable nutation. The apparent sidereal time is therefore subject to an additional non-uniformity compared to the (itself already non-uniform) mean sidereal time, whose main component varies with a period of 18.6 years and an amplitude of ±1.05 seconds.

The hour angle of the vernal equinox is the same for observers located at the same longitude, but different for observers at different longitudes. The sidereal time derived from this is therefore a local time. The sidereal time of the reference location Greenwich is the Greenwich sidereal time. It is particularly often used in calculations. The different types of sidereal time are often designated by their English abbreviations:

• LAST: local apparent sidereal time, apparent local sidereal time
• LMST: local mean sidereal time, mean local sidereal time
• GAST: Greenwich apparent sidereal time, apparent Greenwich sidereal time
• GMST: Greenwich mean sidereal time, mean Greenwich sidereal time

The hour angle of the vernal equinox is the angle counted along the celestial equator from the meridian to the vernal equinox. The right ascension of a star, on the other hand, is the angle counted along the celestial equator from the vernal equinox to the star. If the star is on the meridian (that is: culminating), both angles are equal. It follows: At the moment of culmination of a star, the sidereal time is equal to the right ascension of the star.

The sidereal time is the right ascension in the upper culmination.

This can be used to directly determine the right ascension of the star by observing the culmination time. This is the reason why the right ascension is often given in time units instead of angular units: it is then directly the sidereal time read at the time of culmination. Wega, for example, has a right ascension of 18h 36m 56s, so it will always culminate at 18h 36m 56s local sidereal time.

On the other hand, by observing the culmination of a star of known right ascension, the instantaneous sidereal time can be determined: When Vega culminates, the sidereal time is 18h 36m 56s (in practice, corrections for precession, proper motion, parallax, etc. must still be applied).

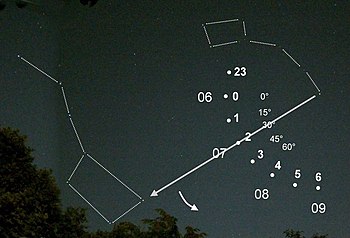
1. the "sidereal hour hand" rotates on a dial fixed on the horizon: after a 15° turn (scale 0°, 15°, 30°, ...) one sidereal hour (scale 23, 0, 1, ...) has passed. 2. the "sidereal hour hand" rotates on a dial dragged along by the sun around the pole star: after about one month (scale 06, 07, 08, ...) one sidereal hour has passed. 2. the "sidereal hour hand" turns on a dial dragged along by the sun and rotating around Polaris: after about one month (scale 06, 07, 08, ...) it has moved ahead of the sun by 30° (scale 0°, 15°, 30°, ...).

Rotation of the starry sky

Daily rotation

One can imagine the starry sky as a large clock disk, which rotates once around itself in a counterclockwise direction (in the northern hemisphere) on a starry day. In the picture, this disk is marked with a hand between Polaris and the Great Bear. The 24-hour dial (scale 23, 0, 1, ...) is fixed at the horizon. If the hand has turned 15° further (scale 0°, 15°, 30°, ...), one sidereal hour has passed. For a solar time hour it must turn slightly further.

Annual rotation

On a dial dragged along by the sun and rotating around the pole star, one notices a very slow advance of the hand. The hand circles it once a year: 30° (scale 0°, 15°, 30°, ...) in about one month (scale 06, 07, 08, ...).

The picture was taken in early July (numeral 07) around 2:00 am. Two hours later (about 4:00) the Big Dipper has moved on to the number 4. One month later in August (number 08) it is already at the number 4 at 2:00 o'clock.