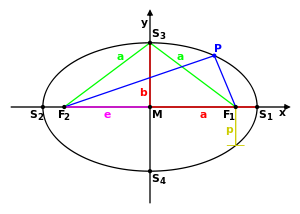
Semi-major and semi-minor axes

The two characteristic radii of an ellipse are called semi-axes:

  • The major semi-axis is half of the largest diameter of an ellipse, which is also called the major axis.
  • The minor semi-axis is half of the shortest diameter (minor axis) and is exactly at a 90° angle to the major semi-axis.

The circle is a special ellipse where these two semi-axes are of equal length, in this case both semi-axes correspond to the radius of the circle.

The major axis (the largest diameter, here \overline {S_{1}S_{2}}) and the minor axis (the smallest diameter, here \overline {S_{3}S_{4}}) are also collectively referred to as the major axes of the ellipse. Major and minor axes are conjugate diameters. This relationship is preserved even when the ellipse is viewed "obliquely", which can be used to geometrically construct other conjugate diameters.

Zoom

Parameters of an ellipse:

S1,S2

Main title

S3,S4

Parting

\overline {S_{1}S_{2}}

Main axis

\overline {S_{3}S_{4}}

Minor axis

a

Large semi-axis

b

Small half-axis

F1,F2

Focal point (ellipse)

e

lin. Eccentricity

M

Center

p

Parameter (semi-latus rectum)

Astronomy

In astronomy, the major semimajor axis of a Keplerian orbit is one of the six so-called orbital elements and is often also inaccurately specified as "mean distance" and usually abbreviated as a. It characterizes - together with the eccentricity - the shape of elliptical orbits of various celestial bodies.

Such bodies are first of all the planets and their moons, artificial earth satellites, the asteroids and thousands of double stars.

According to Kepler's third law, the orbital period U of an elliptical orbit is coupled with a ( {\displaystyle U^{2}/a^{3}=\mathrm {const} }). The constant is related to the mass of the central body - so in a planetary system, it is related to the mass of the central star.

The two main vertices are called apsides, the main axis is the apside line: When a body lies at the focal point F1 and a smaller body orbits it on an ellipse, the shortest distance ( {\displaystyle {\overline {S_{1}F_{1}}}}= a-e) is called the periapsis, and the longest distance ( \overline {S_{2}F_{1}}= a+e) is called the apoapsis (perihelion, aphelion for the Sun).

In the periapsis (pericenter, main vertex close to the gravicenter) the orbital velocity is maximal, in the apocenter minimal.

In addition to the major semimajor axis, the actual mean distance depends on the numerical eccentricity ε \varepsilon=e/aand is

{\displaystyle a\cdot \left(1+{\frac {\varepsilon ^{2}}{2}}\right)}

Geodesy

In geodesy, the axes of the so-called error ellipses are an important means of representing the mean or maximum/minimum point errors. In the adjustment of geodetic networks, the accuracy with which the individual survey points of the network are determined can be represented as an error ellipse.


AlegsaOnline.com - 2020 / 2023 - License CC3