Search algorithm
This article describes searching for data in the context of computer science. For the search for missing persons and ships, see Search Patterns.
This article or subsequent section is not sufficiently supported by evidence (e.g., anecdotal evidence). Information without sufficient evidence may be removed in the near future. Please help Wikipedia by researching the information and adding good supporting evidence.
In computer science, a search procedure or search algorithm refers to an algorithm that searches for patterns or objects with certain properties in a search space. A distinction is made between simple and heuristic search algorithms. Simple search algorithms use intuitive methods for searching the search space, while heuristic search algorithms incorporate knowledge about the search space (for example, the data distribution) to reduce the required search time.
The solution of an algorithmic problem can be generally understood as a search for the solution in a set of possible solutions (the solution space). The solution can be the goal state, but also the path to the goal or the sequence of corresponding actions. If the search space is finite, the search can always lead to a result with an appropriate search strategy. In the case of infinite (solution) sets, the search must be terminated according to certain criteria (e.g. after a certain time).
Repeated searches in a finite set can be made efficient by creating an index structure over the data (e.g. in the form of a search tree) that is sorted according to a certain criterion. Then, when searching, it is no longer necessary to look at all entries (e.g., one starts the search in a telephone directory at the letter with which the name begins).
Simple search algorithms
Simple search algorithms neglect the specific nature of the problem at hand. Therefore, they can be implemented more generally and abstractly, allowing the same implementation to be used for a wide range of problems. The disadvantage of simple search algorithms is the cost incurred: The search space of search problems is generally very large, but simple search only runs in small search spaces in acceptable time.
Search in lists
Algorithms for searching in lists are the simplest search algorithms of all. The goal of searching in lists is to find a particular element of a list of which the associated search key is known. Since this problem is often encountered in computer science, the algorithms used - as well as their complexity - are very well studied.
The simplest search algorithm for lists is the linear search. It traverses one element after the other until an element with the searched key is encountered. The linear search has a running time of 
(n is the number of elements in the list) and can be applied to both sorted and unsorted lists. An advanced method is binary search with a running time of 
. For large lists, it is much more efficient than linear search, but it assumes that the list has been sorted beforehand and that random access to the elements is possible. Interpolation search, also called interval search, is an improvement on binary search that assumes the data is uniformly distributed. The running time 
is better than that of binary search only for very large data sets. Another search algorithm for lists is the Grover algorithm, which is used on quantum computers and runs quadratically faster than classical linear search for unsorted lists. Hashing can also be used for list searching, which takes a constant time average. 
but takes linear time in the worst case.
Search in trees
Searching in trees is the supreme discipline among search algorithms. It searches nodes of trees, regardless of whether the tree is explicit or implicit (generated during the search). The following principle is applied: A node is taken from a data structure. Its child nodes are examined and, if necessary, added to the data structure. Depending on the selection of the data structure, the tree can be searched in different orders. Using a queue leads to a breadth-first search in which the tree is traversed level by level. When using a stack, on the other hand, the system searches up to one leaf at a time and only then continues with the next child node. This is called a depth-first search.
Search in graphs
Many problems in graph theory can be solved using search algorithms. Examples of these problems are the traveling salesman problem, the computation of shortest paths, and the construction of a minimal spanning tree. The corresponding algorithms are for example Kruskal's algorithm, Dijkstra's algorithm or Prim's algorithm, which can be seen as extensions of the algorithms for searching trees.
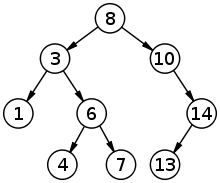
A binary search tree of size nine and depth three
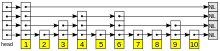
Search in a skip list
Heuristic (Informed) search algorithms
Strategies that can speed up the process of finding solutions are called heuristics. Typical heuristics are rules of thumb, orientation on examples, and emulation of the human problem-solving process. Accordingly, procedures can be divided into uninformed (also called blind search) and informed (use of heuristics). The study of different methods for heuristic search, the development and implementation of new methods and their application to different problem areas are usually counted as the algorithmic core of artificial intelligence. This includes, for example, automatic reasoning, the control of robots and, as typical representatives, especially games. This includes two-person games (zero-sum games with complete information) such as chess, checkers, and mills, as well as one-person games such as sliding puzzles or solitaire. The classical methods for heuristic search are A*, IDA*, bidirectional search schemes, the minimax method, alpha-beta search.
Heuristic search algorithms are also used when an algorithm for solving a problem is too computationally intensive. In this case, a certain error is accepted - i.e. a non-optimal solution is also accepted - if the computing time used can be significantly reduced in return.
Questions and Answers
Q: What is a search algorithm?
A: A search algorithm is a method for finding a target value within a list.
Q: How does a search algorithm work?
A: A search algorithm checks each element of the list for the target value until a match is found or until all the elements have been searched.
Q: Is linear search practical?
A: Linear search is rarely practical because other search algorithms and schemes allow faster searching for all but short lists.
Q: What are some other search algorithms besides linear search?
A: Some other search algorithms are binary search algorithm and hash tables.
Q: Are other search algorithms faster than linear search?
A: Yes, other search algorithms like binary search algorithm and hash tables are significantly faster than linear search for all but short lists.
Q: Why is linear search not the ideal search algorithm?
A: Linear search is not the ideal search algorithm because other search algorithms and schemes allow significantly faster searching for all but short lists.
Q: What is binary search algorithm?
A: Binary search algorithm is a search algorithm that works by repeatedly dividing the search interval in half until the target value is found or until it is confirmed that the target value is not in the list.
