Riemann zeta function

The Riemann zeta function, also known as the Riemann ζ-function or Riemann zeta function (after Bernhard Riemann), is a complex-valued, special mathematical function that plays an important role in analytical number theory, a branch of mathematics. It was first considered in the 18th century by Leonhard Euler, who investigated it within the framework of the Basel problem. It is usually denoted by the symbol $\zeta (s)$ (with the letter zeta), where is a complex number of its domain.

For values $s\in \mathbb {C}$ with real part greater than 1, the Riemann zeta function is defined via a Dirichlet series. By means of analytic continuation, it can be transformed into a Dirichlet series based on $\mathbb {C} \setminus \{1\}$ holomorphic function. It satisfies an important functional equation, which can even be used to characterise it.

Of great importance for number theory is that the zeta function expresses the law of the unique decomposition of natural numbers into prime factors (by this is meant the decomposition of a number into "indivisible" elements, approximately 132 = 2 - 2 - 3 - 11) analytically, i.e. through a closed formula. On this basis, Riemann was able to prove in 1859 the very close and non-obvious relationship between the prime numbers and the position of the zeros of the zeta function. Thus, it follows from the fact $\zeta (s)\neq 0$ for all complex numbers with $\operatorname {Re} (s)\geq 1$ already that the th prime number $p_{n}$ $n\log(n)$ has "quite exactly" the value - more precisely, it follows that

$\lim _{n\to \infty }{\frac {p_{n}}{n\log(n)}}=1.$

Here denotes $\log(n)$ the natural logarithm of . More precise information about zero-free areas makes the picture around the prime number distribution clearer. The Riemann conjecture, which is still unproven (as of September 2020), states that all non-trivial zeros of the Riemann zeta function 1/2 have the real part , i.e. lie on a common straight line. Whether this conjecture is true is one of the most important unsolved problems in mathematics. Because of the importance of prime numbers for modern cryptosystems (such as RSA encryption), the Riemann conjecture also enjoys attention outside pure number theory.

The behaviour of the Riemann zeta function is valid in the ranges $\operatorname {Re} (s)\geq 1$ and $\operatorname {Re} (s)\leq 0$ are understood to be largely. However, their properties within the critical strip $0<\operatorname {Re} (s)<1$ largely unknown and subject to significant conjecture. Among other things, this concerns the questions of asymptotic growth in the imaginary direction and the zero distribution, which is so important for number theory. According to current knowledge, the zeta function in the strip $1/2<\operatorname {Re} (s)<1$ chaos. The values of the zeros not only build bridges to the theory of prime numbers, but most likely also to modern quantum physics. Other areas of application are probability theory and the theory of automorphic forms (especially in the field of the Langlands programme).

From the point of view of algebraic number theory, the Riemann zeta function is only a special case of a whole class of so-called L-functions. Thus it corresponds to the Dirichlet L-function belonging to the trivial character modulo 1 and to the number field ${\mathbb {Q}}$ (rational numbers) corresponding to the Dedekind zeta function.

Because of the paramount importance of the Riemann conjecture for number theory and its applications, the subject of the Riemann zeta function remains an area of intensive mathematical research. Decisive progress was made by mathematicians such as Lindelöf, Hadamard, de La Vallée Poussin, Hardy, Littlewood, Selberg, Woronin and Conrey.

Notation: Throughout the article, denotes $\mathrm {i}$ the imaginary unit and $\mathrm {e} =2{,}71828\dots$ denotes the Euler number. Moreover, often used as a complex variable, which is often decomposed into $s=\sigma +\mathrm {i} t$

Furthermore, Landau's O-notation is often used for the specification of error sizes. If two (unrestricted) functions and behave the same for increasing argument, i.e. $\lim _{x\to \infty }f(x)/g(x)=1$ , this is $f(x)\sim g(x)$ notated as

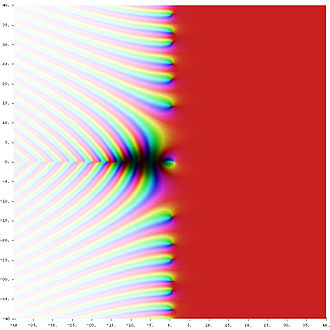
Complex diagram with colouring of the function values: The Riemann zeta function in the complex plane: The zero, i.e. the origin of the complex plane, is located exactly in the middle of the diagram. The so-called non-trivial zeros of the zeta function visible in the picture lie on the vertical line through 0.5 that is not drawn in. They are recognisable as black points on this imaginary line and are arranged in mirror symmetry to the real axis, i.e. to the horizontal line through the origin. The diagram has a single pure white point. This belongs to the only pole of the zeta function in 1, i.e. to that point which is one unit to the right of the origin and in which the zeta function is not defined. The so-called trivial zeros lie on the left part of the real axis, namely in -2, -4, -6, -8 ...

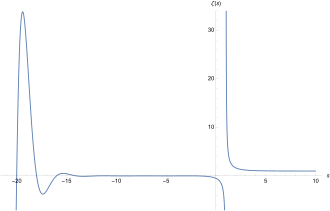
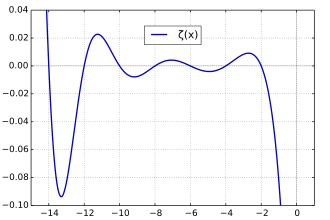
Function graph of the zeta function for real arguments in the range -20 < s < 10

Classification without prior mathematical knowledge

Motivation

At the centre of number theory, that branch of mathematics that deals with the properties of the natural numbers 1, 2, 3, 4 ... are the prime numbers 2, 3, 5, 7, 11 ... These are distinguished by the property of having exactly two divisors, namely 1 and themselves. 1 is not a prime number. Euclid was already able to show that there are an infinite number of prime numbers, which is why the list 2, 3, 5, 7, 11 ... will never end.

The prime numbers are, in a sense, the atoms of the integers, since every positive integer can be unambiguously decomposed into such multiplicatively. For example, 21 = 3 - 7 and 110 = 2 - 5 - 11. Despite this elementary property, after several millennia of mathematical history, there is still no known simple pattern to which the prime numbers conform in their sequence. Their nature is one of the most important open questions in mathematics.

Even if the detailed understanding of sequence 2, 3, 5, 7, 11 ... is unattainably distant, one can look for patterns if one broadens one's view. This is helped, for example, by the idea that statistical methods can often be used to describe the behaviour of a very large number of people (for example, with regard to consumption and voting behaviour) with surprising precision, although a single person is extremely complex. Roughly speaking, this has to do with the fact that increasing amounts of relevant data provide ever more reliable information. In the case of prime numbers, such an expansion leads, among other things, to the question of how many prime numbers there are below a fixed chosen number.

For example, only 4 prime numbers, namely 2, 3, 5 and 7, are smaller than the number 10. In the case of 50, there are already 15 smaller prime numbers, namely

$2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.$

At the end of the 19th century, an amazingly accurate estimate for the distribution of prime numbers was proven as a corollary of the prime number theorem. The prime number theorem was already conjectured in the 18th century by the 15-year-old Gauss (in 1792/93). The estimation was already given before a proof of the prime number theorem by Riemann and appears as a formula that allows the quick calculation of a predicted value. With this formula, for a given number, the number of primes smaller than this number can be estimated in a reasonable time. The formula for prediction becomes more accurate in percentage terms the larger the number is chosen (but with fluctuations). For example, for the value 50 it gives the prediction 14.97 (there are actually 15 primes, see above), making the error 0.16 per cent. Further, it predicts about 78,527 primes below the number 1,000,000 - in fact there are 78,498. This corresponds to a deviation of 0.037 per cent.

One possible tool for proving this formula is the Riemann zeta function. This takes advantage of the fact that it expresses the law of unique prime factorisation in the language of analysis. So the properties of the prime numbers are stored hidden in this function. If the knowledge of the zeta function increases, so does the knowledge of the prime numbers, even in more detailed questions. In this way, many prime number tests, such as Miller-Rabin's, can be proven or improved by assuming the Riemann conjecture.

The zeros of the zeta function generate a correction term of the above formula, which converts it into an exact expression. The resulting exact formula thus knows the distribution of the prime numbers down to the last detail. However, this does not mean that the questions about the prime numbers have been solved: the computational effort increases very strongly with increasing values and thus practical calculations with this formula are not effective. In contrast, modern prime number tests are better suited for numerical research. The exact formula, however, is of theoretical interest: namely, it conceals the error gap between the simple prediction and the actual prime number distribution. It is assumed that this error (within the spectrum of all possibilities) is the smallest possible. Yet deciphering this error would not be so much relevant to numerics. Rather, pure mathematics strives to find out the hitherto hidden reason why the error (if applicable) turns out to be as small as possible.

Prime numbers are not only the subject of basic mathematical research, but also have practical applications. For example, cryptosystems such as RSA encryption use very large prime numbers.

How does the Zeta function "work"?

A mathematical function is basically like a calculating machine. You enter a value into the function and it then delivers a result depending on the input value, at least in theory. What is meant by this is that the function itself does not calculate, but usually only records a calculation rule in the form of a formula. A simple example of a function is the quadratic function, which multiplies the input by itself. This is written formulaically as $f(x)=x^{2}$ . Thus, for example, the quadratic function assigns $-2$ the value $(-2)^{2}$ to the number If this is calculated, the result is $4$ so $f(-2)=4$ .

In principle, the Riemann zeta function works exactly like the example above, except that the calculation rule is a little more complicated. To understand it, the concept of infinite series must be known. A (convergent) series is, roughly speaking, a sum of numbers that never ends and that gets closer and closer to a number. An elementary non-trivial example of a series is based on the number $1/9$ which, in decimal notation, is not closed, but is only closed by the infinite periodic development of a number.

${\frac {1}{9}}=0{,}11111111111\dots$

can be written. If you look more closely, you see that this is just the sum of all reciprocal powers of 10:

${\frac {1}{10}}+{\frac {1}{100}}+{\frac {1}{1000}}+\cdots =0{,}1+0{,}01+0{,}001+\cdots =0{,}111111\dots$

In order for the infinitely long sum to approach a value, it must be ensured that the summands become small "fast enough".

The Riemann zeta function can now be compared to a calculating machine which, for a given number forms the infinite sum of the reciprocals of all natural powers with this exponent. As a mathematical formula, this rule is

${\begin{aligned}\zeta (x)&={\frac {1}{1^{x}}}+{\frac {1}{2^{x}}}+{\frac {1}{3^{x}}}+{\frac {1}{4^{x}}}+{\frac {1}{5^{x}}}+{\frac {1}{6^{x}}}+{\frac {1}{7^{x}}}+{\frac {1}{8^{x}}}+{\frac {1}{9^{x}}}+\cdots \\&=\sum _{n=1}^{\infty }{\frac {1}{n^{x}}}.\end{aligned}}$ .

To understand this better, consider the example of the input x=2 . The natural powers with this exponent are just the square numbers 1, 4, 9, 16, 25 ... . Thus the result of the zeta calculator depending on the input value 2 would be the series

$\zeta (2)={\frac {1}{1}}+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+{\frac {1}{25}}+{\frac {1}{36}}+{\frac {1}{49}}+{\frac {1}{64}}+{\frac {1}{81}}+\cdots .$

It turns out that the expressions $1/N^{2}$ become small fast enough so that this infinite sum approaches a certain numerical value arbitrarily the further one sums. Experimentally, one can state:

$1=1;\qquad 1+{\frac {1}{4}}=1{,}25;\qquad 1+{\frac {1}{4}}+{\frac {1}{9}}\approx 1{,}361;\qquad 1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}\approx 1{,}4236$

and if you even $1.000.000^{2}=1.000.000.000.000$ go up to the millionth square number

$1+{\frac {1}{4}}+{\frac {1}{9}}+\cdots +{\frac {1}{1.000.000.000.000}}\approx 1{,}644933.$

Since a lot of terms have already been added here, one can assume that $1{,}644933$ already quite close to the exact result. The exact limit, as Leonhard Euler was able to justify, is the number

${\frac {\pi ^{2}}{6}}=1{,}644934066848226436472415\dotso$ .

Here π is $\pi =3{,}1415926\dots$ the circular number. Although Euler knew the beginning of the decimal sequence $1{,}64493406684822\dotso$ but its justification was ultimately based on mathematical arguments and not explicit calculations, since the sum never ends. Thus, for input 2, the zeta function returns the result π $\pi ^{2}/6$ . Similarly, for the input 3, 4 ... etc. the reciprocals of all cubic numbers, biquadrat numbers etc. must be added accordingly and new limit values $\zeta (3)$ , $\zeta (4)$ ... etc. come about.

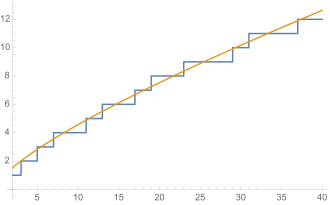
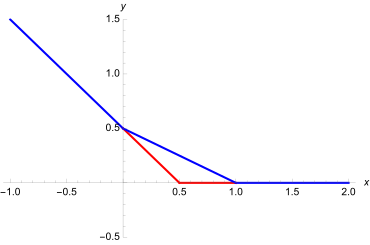
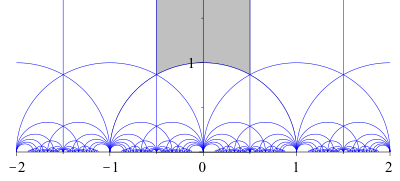
For each prime number, the counting function takes one step up an infinitely long and high staircase. The prediction "meanders" steadily around the counting function. However, for very large values, an ever greater distance between the staircase and the prediction is to be expected.

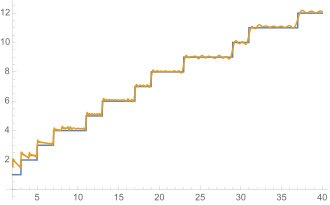
The zeros of the zeta function correct the prediction to an exact term. The more of the infinitely many zeros are included, the more accurate the approximation. The picture shows the correction of 100 pairs of zeros.

History

In contrast to prime numbers or Euclidean geometry, the mathematical history of the discovery of the Riemann zeta function is very young. Thus, all the discoveries concerning this function that are still significant today were made in the last 250 years. On the one hand, the early discovery in relation to the emergence of rigorous (complex) analysis can be justified by the simplicity of the series. On the other hand, the late results can be explained by the difficulty of their properties.

Around 1735 Leonhard Euler solved the Basel problem

One of the first mathematicians to deal intensively and in detail with a precursor of the zeta function as defined today was Leonhard Euler. Since the middle of the 17th century, mathematicians had been trying to find the exact limit of the infinite series.

$1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+\dotsb$

to determine. Personalities such as Pietro Mengoli, who formulated the Basel problem (as it was later called) for the first time, but also Jakob I Bernoulli failed with their attempts to solve it. It was not until around 1734 that Leonhard Euler found the solution.

$1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\dotsb ={\frac {\pi ^{2}}{6}}=1{,}6449340668\dots$

with the circle number π $\pi =3{,}14159265\dots$ , by developing a novel technique for calculating the sine function. However, this proof was not initially accepted by his contemporaries after publication. He then countered with the publication of an alternative proof in 1741. Naturally, Euler was soon involved in the study of series of the type

$f(n)=1+{\frac {1}{2^{n}}}+{\frac {1}{3^{n}}}+{\frac {1}{4^{n}}}+{\frac {1}{5^{n}}}+\dotsb$

interested. He had the hope of being able to make further and, moreover, far more significant statements. And indeed, it was not to remain only with the solution of the Basel problem. Among other things, he found the formulas

$f(4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+{\frac {1}{4^{4}}}+{\frac {1}{5^{4}}}+\cdots ={\frac {\pi ^{4}}{90}},$

$f(6)=1+{\frac {1}{2^{6}}}+{\frac {1}{3^{6}}}+{\frac {1}{4^{6}}}+{\frac {1}{5^{6}}}+\cdots ={\frac {\pi ^{6}}{945}},$

which were first published in 1735 in his work De Summis Serierum Reciprocarum. Although the function values become more complicated with increasing input numbers, Euler calculated the value by hand

$f(26)=1+{\frac {1}{2^{26}}}+{\frac {1}{3^{26}}}+{\frac {1}{4^{26}}}+{\frac {1}{5^{26}}}+\dotsb ={\frac {1.315.862}{11.094.481.976.030.578.125}}\pi ^{26}.$

In his book Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, published in 1755, he finally proved a general formula for $f(2n)$ . This showed that indeed any can $f(2n)$ always be $\pi ^{2n}$ written as a rational multiple of the power π He was not successful, however, with odd arguments, for example, with the series

$f(3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+{\frac {1}{5^{3}}}+\dotsb ,$

because none of his techniques could be applied here. However, he calculated the values $f(2n+1)$ for $n=1,\dotsc ,5$ to several decimal places. He also wrote uniformly $f(n)=N\pi ^{n}$ where rational in the case where an even number. In the case where is odd, Euler conjectured that is "a function of $\log(2)$ ". However, regardless of Euler's vague formulation, this could not be confirmed until today. The values of the series for odd arguments greater than 1 are still (as of 2020) largely unknown and the subject of number-theoretical conjecture.

Euler is considered the discoverer of the link between the zeta function and the prime numbers. This link is still called the Euler product today. Thus he wrote in his work Variae observationes circa series infinitas:

"If the following expression is formed from the series of prime numbers ${\frac {2^{n}}{2^{n}-1}}\cdot {\frac {3^{n}}{3^{n}-1}}\cdot {\frac {5^{n}}{5^{n}-1}}\cdot {\frac {7^{n}}{7^{n}-1}}\cdot {\frac {11^{n}}{11^{n}-1}}\cdot \mathrm {etc}$ , its value will be equal to the sum of this series $1+{\frac {1}{2^{n}}}+{\frac {1}{3^{n}}}+{\frac {1}{4^{n}}}+{\frac {1}{5^{n}}}+{\frac {1}{6^{n}}}+{\frac {1}{7^{n}}}+\mathrm {etc}$ “

- Leonhard Euler

Immediately Euler was aware of the relationship between prime numbers and geometry, and he continued writing:

"Because after setting $n=2$ holds $1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+\mathrm {etc} ={\frac {\pi ^{2}}{6}}$ , where π $\pi$ denotes the periphery of the circle whose diameter is 1, will be ${\frac {4\cdot 9\cdot 25\cdot 49\cdot 121\cdot 169\cdot \mathrm {etc} }{3\cdot 8\cdot 24\cdot 48\cdot 120\cdot 168\cdot \mathrm {etc} }}={\frac {\pi ^{2}}{6}}.$ “

- Leonhard Euler

From the fact, already well known at that time, that the harmonicseries is divergent, Euler was also able to conclude from the Euler product that the sum of the reciprocals of all prime numbers has no finite limit. This result is also known as Euler's theorem on the summation of the reciprocals of the primes.

The functional equation later proved by Riemann was also already known to Euler. In his work Remarques sur un beau rapport entre les series des puissances tant directes que reciproques, he described it in a mathematically non-rigorous way:

"Par cette raison je hazarderai la conjecture suivante, que quelque soit l'exposant n, cette équation ait toujours lieu:

${\frac {1-2^{n-1}+3^{n-1}-4^{n-1}+5^{n-1}-6^{n-1}+\cdots }{1-2^{-n}+3^{-n}-4^{-n}+5^{-n}-6^{-n}+\cdots }}={\frac {-1\cdot 2\cdot 3\cdot 4\cdot (n-1)(2^{n}-1)}{(2^{n-1}-1)\pi ^{n}}}\cos {\frac {n\pi }{2}}.$ “

"For this reason I venture to suggest the following conjecture that for any variable n the following the equation is always valid:

${\frac {1-2^{n-1}+3^{n-1}-4^{n-1}+5^{n-1}-6^{n-1}+\cdots }{1-2^{-n}+3^{-n}-4^{-n}+5^{-n}-6^{-n}+\cdots }}={\frac {-1\cdot 2\cdot 3\cdot 4\cdot (n-1)(2^{n}-1)}{(2^{n-1}-1)\pi ^{n}}}\cos {\frac {n\pi }{2}}.$ “

- Leonhard Euler

Euler was actually referring to Dirichlet's eta function, which, however, corresponds to the Riemann zeta function except for one factor. Euler did not give a rigorous proof of a functional equation, but had only checked it for many values and then assumed it to be universally valid.

Dirichlet shows his prime number theorem

In 1838, the mathematician Peter Dirichlet made a major contribution to number theory. He proved a conjecture of Fermat, which is now called Dirichlet's prime number theorem. This states that every arithmetic progression $ak+b$ with positive, divisor-alien $a,b$ contains infinitely many prime numbers. For example, if $a=4$ and it $b=1$ follows that the list contains 1, 5, 9, 13, 17 ... infinitely many prime numbers.

The key to the proof was, in addition to the Riemann zeta function, a whole class of other functions that also decompose into prime products and thus form a "large family". Only a century later, thanks to finer methods, Dirichlet's results could be clearly specified by Siegel and Walfisz (Siegel-Walfisz theorem).

Riemann's contribution to the zeta function

In 1859, Bernhard Riemann decisively elaborated the connection of the zeta function to the prime numbers already given by Euler in his publication Über die Anzahl der Primzahlen unter einer gegebenen Größe. The great achievement was to recognise the relevance of extending the domain of definition to complex numbers. Only with this approach had it become possible to gain concrete information about primes 2, 3, 5, 7 ... themselves. This is remarkable insofar as prime numbers are real numbers. Riemann, who was a student of Carl Friedrich Gauss, wrote a function-theoretical interpretation and evaluation of the Euler product in his ten-page paper, which created a connection between prime numbers and the non-trivial zeros of the zeta function. The main result was a formula that counted the number of prime numbers under a given (non-integer) positive number without any error. With this, he had managed a completely new approach to the theory of prime numbers.

In his work he established the Greek $\zeta$ (zeta) as a function symbol and also formulated the Riemann conjecture, named after him and unproven to this day, which asserts an important statement about the exact location of the zeros of the zeta function.

Although the article is nowadays seen as a breakthrough and departure for modern analytical theory around the zeta function, it was far from being met with enthusiasm in mathematical circles at the time. This was primarily due to the fact that Riemann had omitted to provide proofs for his formulas in most places. As a result, Godfrey Harold Hardy and John Edensor Littlewood described Riemann's work merely as a "remarkable collection of heuristic insights", although English mathematicians were still so backward in analytical number theory at the beginning of the 20th century that Littlewood remembered being given Riemann's conjecture as an exercise by his professor in 1906. Edmund Landau was also among the most vocal critics regarding the meaning of the article. Although he initially called it "brilliant and fruitful", his praise soon changed:

"Riemann's formula is by no means the most important thing in the theory of prime numbers. He created some tools which, once worked out, will make some other proofs possible."

- Edmund Landau

Detlef Laugwitz notes in his Riemann biography that Landau also paid little tribute to Euler's groundbreaking work in his textbooks, as he tended to appreciate only work in which every detail was worked out. On the other hand, mathematicians like Felix Klein admired that Riemann had worked "with great general ideas" and "often relied on his intuition". That was even before Carl Ludwig Siegel's study of the estate showed how extensive Riemann's analytical work on the zeta function was. The calculations in the estate were difficult to decipher, however, and it took a mathematician of Siegel's calibre to reconstruct Riemann's ideas.

Riemann did not work on the zeta function again from this time until his early death (he died of tuberculosis at the age of just 39); it remained his only publication on number theory. The 1859 essay was only sketchy; Riemann wanted to thank the Berlin Academy of Sciences for admitting him.

Many of Riemann's records were burned by his housekeeper after his demise until she was stopped by members of the Göttingen faculty. The remaining writings were handed over to his widow and thus disappeared for many years. To this day, we can only speculate about further results on the Zeta function that would have been found if the documents had not been partially destroyed.

The last years of the 19th century

Mangoldt proves Riemann's main formula

In 1893, the mathematician Jacques Hadamard published a paper that laid the foundation for a more detailed understanding of Riemann's work. Hadamard had succeeded in proving a formula for the zeta function that included its zeros. Strictly speaking, this was a procedure for constructing the zeta function as a whole from its zeros. The existence of such a formula had already been assumed by Riemann, but had not been rigorously proved until then. For the verification of Riemann's ideas, however, it was a substantial part: the basic scheme of argumentation for Riemann's main formula was namely "prime product (Euler) versus zero product (Riemann/Hadamard)". For this reason, among others, Hans von Mangoldt called Hadamard's contribution "the first real progress in this field for 34 years".

Building on Hadamard's work, Hans von Mangoldt made the breakthrough to Riemann's main formula only two years later, in 1895. However, he showed it in a slightly modified version that is considered more "natural" today. In honour of his achievement, the main formula is now called the Riemann von Mangoldt formula.

Hadamard and De La Vallee-Poussin prove the prime number theorem

After von Mangoldt proved Riemann's main formula in 1895, not much was needed to prove the prime number theorem. This theorem makes a statement about how often prime numbers appear on average. All that remained was to show that the zeta function has no zeros in the range in which Euler's prime number product is "just not valid any more". Independently, Hadamard and the Belgian Charles-Jean de La Vallée Poussin produced the proof in 1896. Important points for the proof were ideas of Franz Mertens and the trigonometric identity $3+4\cos(\theta )+\cos(2\theta )=2(1+\cos(\theta ))^{2}$ .

Although there was great excitement in the mathematics world, there were concerns about the naturalness of the method of proof, which was strongly tied to the properties of the difficult zeta function. It was considered strange that a statement about prime numbers was even equivalent to a certain distribution of the zeros of a complex function. Thus Albert Ingham expressed in 1932:

"One may consider the proof of the prime number theorem, [...] of de la Vallée Poussin and Hadamard unsatisfactory, because terms are introduced which are very far from the original problem. Therefore it is only too natural to ask for a proof which does not depend on the theory of functions of a complex variable. To this we must reply that at present no such proof is known. Indeed, we may go further and say that it is unlikely that a truly real proof will be found; at least it is unlikely so long as the theory relies on the Eulerian identity. For every known proof of the prime number theorem relies on some property of the complex zeros of $\zeta (s)$ and, conversely, this property is a simple corollary of the prime number theorem itself. It seems clear, therefore, that this property must be used explicitly or implicitly in any proof $\zeta (s)$ based on and one does not see how a proof is to be given using only the real values of "

- Albert Ingham

In 1948, an elementary proof (i.e. one that does not require any functional theory) was finally given by Atle Selberg and Paul Erdös. However, "elementary" does not mean "simple". In the course of time, considerably simpler function-theoretic and elementary proofs of the prime number theorem were found.

Beginning of the 20th century

Hilbert formulates his 23 problems

→ Main article: Hilbert problems

David Hilbert gave a lecture on 8 August at the 2nd International Congress of Mathematicians in Paris in 1900. In it, he formulated a list of 23 mathematical problems that he considered to be among the most important of the coming century. At that time, Hilbert was already one of the leading mathematicians of the day. Problem No. 8 was the Riemann conjecture:

"In the theory of the distribution of prime numbers, considerable progress has been made in recent times by Hadamard, De La Vallee-Poussin, V. Mangoldt and others. However, for the complete solution of the problems posed to us by Riemann's treatise 'On the Number of Primes under a Given Quantity', it is still necessary to prove the correctness of Riemann's extremely important assertion that the zeros of the function $\zeta (s)$ $\textstyle \zeta (s)=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+\cdots$ represented by the series all have the real component ${\tfrac {1}{2}}$ - if one disregards the known negative integer zeros. As soon as this proof is successful, the further task would be to test the Riemann infinite series for the number of primes more precisely and, in particular, to decide whether the difference between the number of primes below a magnitude and the integral logarithm of } does indeed become infinite of no higher than the $\tfrac12$ {1}{2}}th order in and further, whether then the members of Riemann's formula depending on the first complex zeros of the function $\zeta (s)$ really cause the local compression of the primes which has been noticed in the counts of the primes.“

- David Hilbert

The high reputation Hilbert enjoyed inspired mathematicians to tackle his problems, including the zeta function. To date, 15 of the 23 problems are considered solved, but not the Riemann conjecture.

Ramanujan's work on the zeta function

In 1910, the Indian mathematician Srinivasa Ramanujan published an article in the Journal of the Indian Mathematical Society in which, among other things, the following equation was asserted:

$1+2+3+4+5+\dotsb =-{\frac {1}{12}}.$

Most mathematicians who had seen this equation had judged it to be obvious nonsense. So it was that Professor Hill of University College in London wrote:

"Mr Ramanujan has become a victim of the pitfalls of the very difficult field of divergent series."

- Micaiah John Muller Hill

Hill, however, was not completely dismissive and encouraged Ramanujan to keep trying. And so he sent his results directly to some mathematicians at Cambridge. Two of them were unable to recognise the statements behind Ramanujan's coded formulae and refused the request for assistance. However, when Ramanujan finally also drew Godfrey Harold Hardy's attention to his ideas by letter, the latter became aware of the correct evaluation of the value $\zeta (-1)$ equation, even though it was of course incorrect in terms of its mathematical formality. In this context, the formula was already known to Euler, since it results from $\zeta (2)$ and the functional equation (both found by Euler). Furthermore, Ramanujan's claim to have a formula that predicts almost flawlessly whether a given number is prime or not (Ramanujan's formula, however, did not use the zeros of the zeta function) aroused much curiosity. Even in a second letter, however, he gave no proof of this. Littlewood expressed:

"This letter could make you furious."

- John Edensor Littlewood

The initially exclusively written exchange eventually culminated in Ramanujan's stay in England, where the duo of Ramanujan and Hardy developed into one of the most productive and extraordinary mathematical correspondences in history.

After the evaluation of Ramanujan's diaries by George E. Andrews and Bruce Berndt, among others, Ramanujan's numerous ideas on the Riemann zeta function were revealed. Thus he independently found Euler's formula for $\zeta (2n)$ the Euler product as well as numerous infinite series and integrals that contain zeta values in whole and also half-integer places.

The Riemann Legacy

Fifty years after Riemann's death, some unburned pages resurfaced. Richard Dedekind, a colleague of Riemann had received some pages of Riemann's wife Elise's estate and deposited some of them in the library of Göttingen. After the mathematics historian Erich Bessel-Hagen found the writings in 1926 and was unsuccessful in his attempt to decipher the confused records, the documents went to Carl Ludwig Siegel. Siegel was astonished by the depth of Riemann's thoughts on the zeta function. This at the same time invalidated much criticism of Riemann's original work, since the notes showed that Riemann's claims were based on thorough calculations. However, Siegel also complained about the chaos in the notes:

"Nothing of what Riemann had written down about the zeta function was ripe for publication. Sometimes you find disjointed formulae on the same page, often only half of an equation."

- Carl Ludwig Siegel

Siegel discovered that Riemann had calculated at least three non-trivial zeros of the zeta function with relative accuracy using only handwritten calculations. The formula used for this was worked out by Siegel, published in 1932 and has since been called the Riemann-Siegel formula.

After 1945 until today

In the age of the computer

See also: History of calculation methods for the Riemann zeta function

In research on the Riemann zeta function, computers are mainly used to check the correctness of the Riemann conjecture for as many zeros as possible. Although all calculations are numerical procedures, they show exactly and not only approximately that the examined zeros are on the critical straight line.

As early as 1936, the Oxford mathematician Edward Charles Titchmarsh had calculated the first 1,041 non-trivial zeros of the zeta function with a machine originally designed for astronomical calculations. In 1953, these calculations were continued by Alan Turing. His method is still used today. For the first time, a computer was used.

From the beginning of the 1980s, computers became more and more powerful. As early as 1979, a group from Amsterdam around Herman te Riele and Richard P. Brent had checked 200 million zeros (a little later they increased their calculation to 300 million) - all of them were on the critical straight line. In doing so, they contradicted a prediction by Don Zagier, who had said that it would be "a miracle" if they were still all on the critical straight line. Zagier referred to theoretical reasons, which confirmed the position of the first few thousand zeros on the straight line, but were weaker for increasing numbers - and ultimately even argued against it.

By 2005, the first 900 billion zeros had been checked by distributed computers as part of the so-called ZetaGrid Project. Around the same time, Xavier Gourdon, with the support of Patrick Demichel, calculated the first 10 trillion ( $10^{{13}}$ ) zeros. All of them lay on the critical straight line.

Number theory meets quantum physics

In 1972, a coincidental conversation between the physicist Freeman Dyson and the mathematician Hugh Montgomery revealed a previously unnoticed connection between quantum physics and number theory. The subject of the discussion was the zeros of the Riemann zeta function. In their distribution, which was assumed by Montgomery, Dyson recognised the distances between pairs of eigenvalues of Hermitian random matrices. These are used by quantum physicists to predict the energy levels in a heavy atomic nucleus when it is irradiated with low-energy neutrons. When Montgomery looked at the distances between the energy levels in the atomic nucleus erbium, the 68th element in the periodic table, he recognised a striking similarity. The general agreement between a certain section of the zero locations on the critical line and the experimentally determined energy levels was highly significant.

Through extensive use of computers, Montgomery's conjecture about Andrew Odlyzko's zero distances was verified. The numbers were in favour of Montgomery's assumption. Odlyzko published his results in 1987.

Despite strong evidence, some were sceptical about the results. The question arose whether any progress had been made in pure mathematics. For example, the number theorist Peter Sarnak from Princeton said:

"After all, it's quite fascinating to see the same images in both fields, but who can name a real contribution to number theory that this has made possible?"

- Peter Sarnak

Jonathan Keating, a student of the physicist Michael Berry, soon provided a number-theoretical application. Berry had previously worked on connections between prime numbers and quantum physics (especially connections to quantum chaos). But it was eventually Keating and his PhD student Nina Snaith who, using statistical methods (often used in quantum physics), established an exact formula for the average behaviour of powers of absolute values of the zeta function along the critical straight line. These averages are important for number theory and have many applications, for example to Dirichlet's divisor problem. A few minutes before Keating presented his results, he and Snaith had "tested" the formula on a blackboard by seeing if a result they had already laboriously worked out would be correctly predicted. What was special about the approach of Keating and Snaith, which was praised by Atle Selberg among others, was that they interpreted prime numbers as random variables, i.e. as the results of a coin toss. Sarnak conceded that without this strange approach, such a conjecture about the zeta function could not have been worked out.

Montgomery's pair correlation conjecture and the asymptotic behaviour of the zeta moments are still the subject of intensive research today.

The Riemann conjecture until today

See also: History of the Riemann Conjecture

At the latest after Hilbert included the Riemann conjecture on his list of problems, it aroused the interest of numerous mathematicians. But to this day, the problem proves to be extraordinarily difficult.

After Atle Selberg showed in 1942 that a positive proportion of the zeros must lie on the critical straight line, a real race developed to find the size of this proportion. Norman Levinson showed that a good third fulfil the assumption, and Brian Conrey showed in 1989 that it is even a good 40 percent. Whether these methods ultimately lead to a solution, however, is considered controversial. Not even such a proof that "100 per cent" (in an asymptotic sense) of the zeros obey the conjecture would be necessarily purposeful, since the number of zeros is infinitely large. Similar concerns exist about the efforts made to optimise zero-free regions.

Stephen Smale, winner of the Fields Medal, published his own list of 18 problems in 1998, written in the spirit of Hilbert. Problem number 1 is the Riemann conjecture. So far, only a few problems on Smale's list have been solved (see Smale problems).

The Riemann conjecture gained further fame when it was placed on the list of millennium problems by the Clay Mathematics Institute (CMI) in 2000. A prize of 1 million US dollars is offered for a conclusive proof.

Considered a pioneer of modern theory around the zeta function: Bernhard Riemann

Bernhard Riemann's original work

David Hilbert formulated 23 mathematical problems, the eighth of which was the Riemann conjecture

Had self-taught enormous knowledge of zeta function: Srinivasa Ramanujan

Considered one of the 20th century's leading experts in the field of random matrices: Freeman Dyson

Initially became involuntarily involved in a conversation with Dyson at the insistence of Sarvadaman Chowla: Hugh Montgomery

Found that his greatest mathematical discovery was "Ramanujan": Godfrey Harold Hardy

Was able to comprehensibly prepare large parts of Riemann's preserved records for posterity: Carl Ludwig Siegel

Euler's explicit calculations in his original work De Summis Serierum Reciprocarum

Peter Dirichlet showed with the help of the zeta function that number sequences such as 1, 5, 9, 13, 17, 21 ... or 7, 107, 207, 307, 407 ... contain an infinite number of prime numbers.

Leonhard Euler, 1753

Practical areas of application

Applications with practical relevance are given below. Relationships to basic mathematical and physical research can be found below in the areas:

Analytic number theory
Algebraic number theory
Automorphic shapes
Geometry
Probability theory and statistics

Fast primality tests

→ Main article: Miller-Rabin test

A prime number test is an algorithm that checks whether a given number is a prime number. If one proceeds completely naively here, one must calculate whether one of the numbers $2,3,\dots ,q$ with ${\sqrt {n}}\leq q<{\sqrt {n}}+1$ divisor of n {\displaystyle n}. If none of these numbers divide then it must be a prime number, since every divisor greater than corresponds to a divisor less than via $rs=n$ . This procedure requires about $O({\sqrt {n}})$ computational operations, since about quotients have to be formed and evaluated. Thus, despite its simplicity, it is considered laborious.

The location of the zeros of the Riemann zeta function plays a role in proving the existence of faster prime tests. Under the assumption of the Generalised Riemann Conjecture, Gary L. Miller was able to show in 1976 that there is a deterministic prime number test which in $O(\log(n)^{4}\log(\log(\log(n))))$ steps (i.e. "quickly") tests whether is a prime number or not. The term Generalised Riemann Conjecture means that not only the Riemann zeta function, but also all Dirichlet L-functions never satisfy for arguments with take $\operatorname {Re} (s)>1/2$ value zero.

In 1980, Michael O. Rabin succeeded in transforming this into a probabilistic test which, although it never gives a result that is 100 per cent correct, is very reliable after a sufficient number of steps. This works independently of the Riemann conjecture.

→ Main article: RSA cryptosystem

Large prime numbers are used in the encryption of data (for example on the internet). The security of such systems is based on the assumption that there is no fast way to decompose a number into its prime factors. In the RSA cryptosystem, a person who wants to encrypt a message takes two large prime numbers and with a large distance between them, and forms the composite number $pq=N$ . With the help of this, messages (if previously converted into numbers) can now be encrypted by a public key generated from and This key is available to everyone, but does not give insight into the cryptosystem itself. With the knowledge of and a message from the public to the private person can subsequently be decrypted again, since with the knowledge of and "counter key" can also be generated, which restores the plaintext. This counter key is only available to the private individual and is therefore a private key. Consequently, to break the system, the factorisation of required.

Physics

In physics, the Riemann zeta function plays a versatile role. Applications have special function values, for example:

The value $\zeta (3/2)\approx 2{,}61237$ is required, among other things, in the calculation of the critical temperature for the formation of a so-called Bose-Einstein condensate and in spin wave theory for magnetic systems.

The value $\zeta (2)\approx 1{,}64493$ is needed in the high temperature limes in the density of states for the harmonic oscillator.

The value $\zeta (5/2)\approx 1{,}34148$ is used in the density of states for a free boson gas.

The constant $\zeta (4)\approx 1{,}08232$ to the integral over the radiance of Planck's blackbody radiation.

In addition, the so-called zeta function regularisation plays a role in the regularisation of divergences in quantum field theory. Similar to what Ramanujan did, finite values are assigned to divergent series. An application example of such a regularisation concerns the Casimir effect.

Ramanujan and Euler's formula for $\zeta (-1)$ can be used heuristically to derive in a simple way the necessity of 26 space-time dimensions in bosonic string theory.

Zipf's Law

→ Main article: Zipf's law

Zipf's law was originally formulated in quantitative linguistics and states that in a corpus of natural language utterances, the frequency of a word is inversely proportional to its rank in the frequency table. Thus, the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, and so on. Using different words, this has a probability distribution of

$P(X=n)={\frac {1}{nH_{N}}}$

with the harmonic sequence $H_{N}$ consequence. However, depending on the type of data set, a different exponent may be needed. With the generalised harmonic sequence $\textstyle H_{N}^{(s)}=1+{\frac {1}{2^{s}}}+\cdots +{\frac {1}{N^{s}}}$ can be used for real parameters the generalised distribution

$P(X=n)={\frac {1}{n^{s}H_{N}^{(s)}}}$

describe. In the case of the zeta distribution suitable for "infinitely many words" $s>1$ thus be generated:

$P(X=n)={\frac {1}{n^{s}\zeta (s)}}.$

Properties of the Dirichlet series

For real arguments σ $\sigma >1$

Imaging properties and conclusions

On the open interval $]1,\infty [$ the zeta function is an unbounded, real-valued and strictly monotonically decreasing function. In particular, it is injective in this domain. Thereby 1 is its largest lower bound, which is why (due to its continuity) it $]1,\infty [$ bijectively maps the interval onto itself. Meanwhile, it follows immediately from its holomorphism that it is real differentiable (i.e. smooth) on $]1,\infty [$ any number of times.

Since $\zeta (]1,\infty [)\subset \mathbb {R}$ , it already follows $\zeta (\mathbb {R} \setminus \{1\})\subset \mathbb {\mathbb {R} }$ . A property of analytic functions is to satisfy a mirror law under complex conjugation under these conditions: It holds $\zeta ({\overline {s}})={\overline {\zeta (s)}}$ . This has important consequences for the zero distribution, since the zeros are mirrored on the real axis and thus occur in pairs.

Inequalities

The real Dirichlet series can be enclosed in its convergence region by rational functions. For all σ $\sigma >1$ estimation is valid

${\frac {1}{\sigma -1}}<\zeta (\sigma )<{\frac {\sigma }{\sigma -1}}.$

Also interesting in this area is the inequality

$\sigma {\frac {\zeta (\sigma )}{\zeta (\sigma +1)}}>(\sigma +1){\frac {\zeta (\sigma +1)}{\zeta (\sigma +2)}}.$

Convergence speed

If we define $\textstyle \zeta _{N}(s)=\sum _{n=1}^{N}{\frac {1}{n^{s}}}$ then for all $\operatorname {Re} (s)>0$

$\zeta (s)-\zeta _{N}(s)={\frac {(N+1)^{1-s}}{s-1}}+{\frac {1}{2}}(N+1)^{-s}+R_{N+1}(s),$

where $\textstyle |R_{N}(s)|\leq {\frac {1}{12}}{\frac {|s(s+1)|}{\sigma +1}}N^{-\sigma -1}$ . This follows from the Euler-Maclaurin summation formula, which can also be used to calculate the zeta function numerically. This shows that the rate of convergence of the Dirichlet series decreases $\sigma >1$ for smaller real parts σ Moreover, it follows that the series $\textstyle \sum 1/n^{s}$ not converge at any point $s=1+\mathrm {i} t$

Behaviour in the vertical and horizontal direction

For real parts that increase indefinitely, the zeta function has an asymptotic behaviour that is easy to determine; the following applies

$\lim _{\operatorname {Re} (s)\to \infty }\,\zeta (s)=1.$

This follows directly from the uniform convergence of the Dirichlet series in the domains $\operatorname {Re} (s)\geq 1+\varepsilon$ and interchanging limes and summation. Compare also the complex graph of the zeta function at the beginning of the article, which is coloured increasingly constant red in the direction of the positive real axis.

For any σ $\sigma \in \mathbb {R}$ with σ

${\frac {\zeta (2\sigma )}{\zeta (\sigma )}}<|\zeta (\sigma +\mathrm {i} t)|<\zeta (\sigma )$

for all $t\in \mathbb {R} \setminus \{0\}$ .

This estimation is optimal. With the Euler product and Kronecker's approximation theorem, the following statements can also be made

$\liminf _{t\to \infty }|\zeta (\sigma +\mathrm {i} t)|={\frac {\zeta (2\sigma )}{\zeta (\sigma )}}\quad {\text{und}}\quad \limsup _{t\to \infty }|\zeta (\sigma +\mathrm {i} t)|=\zeta (\sigma )$

prove. Also with approximation methods it can be proved that for every T > 0 > T such that $\tau >T$

$\sup _{\sigma >1}|\zeta (\sigma +\mathrm {i} \tau )|\geq {\frac {1}{10}}\log(\log(3+\tau ))$

holds. Regarding the averages on vertical lines, Turganaliev showed in 1981 for all σ $\sigma >1/2$ > 1

${\frac {1}{T}}\int \limits _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|\mathrm {d} t=\sum _{n=1}^{\infty }{\frac {d_{1/2}^{2}(n)}{n^{2\sigma }}}+O\left({\frac {1}{\log(T)}}\right).$

Here the coefficients generate $d_{1/2}(n)$ the Dirichlet series to $\zeta (s)^{1/2}$ .

Relationships to number theoretic functions

The Dirichlet series of some elementary and important (very often multiplicative) number-theoretic functions can be expressed via the Riemann zeta function. Of great importance here, for example, is the observation that the multiplicative inverse of the zeta function can again be represented by a Dirichlet series. The formula applies

${\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}=1-{\frac {1}{2^{s}}}-{\frac {1}{3^{s}}}-{\frac {1}{5^{s}}}+{\frac {1}{6^{s}}}-{\frac {1}{7^{s}}}+{\frac {1}{10^{s}}}-\dotsb ,$

where μ $\mu (n)$ denotes the Möbius function here. The series to the right converges (because $|\mu (n)|\leq 1$ for all $n\in \mathbb{N}$ ) absolute on the half-plane $\operatorname {Re} (s)>1$ and, if Riemann's conjecture is correct, even (conditionally) on the half-plane $\operatorname {Re} (s)>1/2$ (which can be seen by means of partial integration). For an informal explanation of the Dirichlet series identity, consider

${\frac {1}{\zeta (s)}}=\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\cdots ,$

i.e. the reciprocal of the Euler product, and forms the associated Dirichlet series by consistent multiplication out.

The Dirichlet convolution for number theoretic functions is a homomorphism from the ring $(A,+,*)$ number theoretic functions into the ring of formal Dirichlet series $(D,+,\cdot )$ . By means of these, further identities result. Important for number theory are, for example, formulas such as

$\zeta (s)\zeta (s-a)=\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}},\quad a\in \mathbb {C} ,$

with the divisor function σ $\sigma _{a}$ or also

${\frac {\zeta (s-1)}{\zeta (s)}}=\sum _{{n=1}}^{\infty }{\frac {\varphi (n)}{n^{s}}}$

with the Eulerian phi function. There is a whole galaxy of other identities beyond that. For example, the formula

${\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}=\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}},\qquad \operatorname {Re} (s)>1+\max\{0,\operatorname {Re} (a),\operatorname {Re} (b),\operatorname {Re} (a+b)\},$

can be traced back to Ramanujan. These identities testify to a close connection between number-theoretic functions on the one hand and a function endowed with good analytic properties such as global meromorphism on the other. By means of methods of analytic number theory, often striking behavioural patterns of these number-theoretic functions can be proved. Two important techniques for this, the Selberg-Delange method and the use of dew theorems, are described in this article.

Dirichlet series of derivatives and root function

Its -th derivative has for arguments with real part greater than 1 the representation

$\zeta ^{{(k)}}(s)=(-1)^{k}\,\sum _{{n=2}}^{\infty }{\frac {(\log n)^{k}}{n^{s}}}.$

This follows by means of limb-wise differentiation, which because of uniform convergence of the series on compact subsets $K\subset \{s\in \mathbb {C} \mid \operatorname {Re} (s)>1\}$ is allowed. Similarly there for a stem function:

$\int \zeta (s)\mathrm {d} s=s-\sum _{n=2}^{\infty }{\frac {1}{n^{s}\log(n)}}+C.$

Function graph of the function $|\zeta (2+\mathrm {i} t)|$ for 0 < t < 2000, this is $\zeta (4)/\zeta (2)$ bounded above by ζ ( 2 $\zeta (2)$ below by ζ ( 4

Special function values

Function values for even natural numbers

Properties

The function values of the Riemann zeta function for positive even numbers have a close relationship to the circle number π $\pi$ . For a positive integer is

$\zeta (2n)=(-1)^{n-1}\,{\frac {(2\pi )^{2n}}{2(2n)!}}\,B_{2n},$

where $B_{2n}$ denotes the -th Bernoulli number. This formula was first discovered by Leonhard Euler. Thus $\zeta (2n)$ for is n > 0 rational multiple of π 2 n $\pi ^{2n}.$ It follows immediately by Lindemann-Weierstrass' theorem that any value $\zeta (2n)$ for natural numbers is irrational and even transcendental.

Derivation to Euler's formula

Euler was inspired in his considerations by the Taylor series of the cardinal sinus. Via comparison of the coefficients on both sides, where on the right side first multiply out,

${\frac {\sin(\pi z)}{\pi z}}=1-{\frac {\pi ^{2}z^{2}}{6}}+{\frac {\pi ^{4}z^{4}}{24}}-\cdots =\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}}}\right)$

he concluded, for example

$\zeta (2)={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\dotsb ={\frac {\pi ^{2}}{6}},\quad \zeta (4)={\frac {\pi ^{4}}{90}},\quad \zeta (6)={\frac {\pi ^{6}}{945}}.$

An alternative and more direct access to the values at even places is provided by the cotangent function. On the one hand, its infinite partial fraction decomposition yields the power series

$\pi z\cot(\pi z)=1-2\sum _{n=1}^{\infty }\zeta (2n)z^{2n},\quad |z|<1,$

on the other hand follows via the complex sine and cosine

$\pi z\cot(\pi z)=\pi \mathrm {i} z{\frac {\mathrm {e} ^{2\pi \mathrm {i} z}+1}{\mathrm {e} ^{2\pi \mathrm {i} z}-1}}=\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2\pi )^{2n}}{(2n)!}}B_{2n}z^{2n}.$

By comparing the coefficients of both power series, Euler's formula is obtained.

More formulas

The recursion formula applies

$\zeta (2n)={\frac {1}{n+{\frac {1}{2}}}}\cdot \sum _{{k=1}}^{{n-1}}\zeta (2k)\cdot \zeta (2(n-k))$

for natural numbers n>1 which was not yet known to Euler.

Application

Although the Bernoulli numbers are rational, their explicit calculation for increasing indices is difficult, since initially only elaborate recursion formulae are available. For a long time, therefore, Euler's formula was valid for the values $\zeta (2n)$ (combined with Staudt-Claus's theorem) as the best basis for calculating the values $B_{2n}$ . However, in 2008 David Harvey found a slightly faster algorithm that does not require the use of the zeta function.

Function values for odd natural numbers

Very little is known about the value of the zeta function for odd natural numbers. The reason for this is that all known methods for explicitly determining values $\zeta (k)$ with $k\geq 2$ actually determine the value of the infinite series

$\sum _{n\in \mathbb {Z} \atop n\not =0}{\frac {1}{n^{k}}}$

which $2\zeta (k)$ has the value for even values but is trivially 0 for odd by truncating the summands, whereby the essential information is lost. Nevertheless, it is known, for example, that the Apéry constant $\zeta (3)$ irrational, which was proven in 1979 by the French mathematician Roger Apéry. His proof attracted a great deal of attention in mathematics circles. Don Zagier described Apéry's proof as a "sensation".

Apéry series

In essence, Apéry used for the proof of the irrationality of $\zeta (3)$ the rapidly convergent series

$\zeta (3)={\frac {5}{2}}\sum _{{k=1}}^{\infty }{\frac {(-1)^{{k-1}}}{k^{3}{2k \choose k}}}$

with rational links. On the other hand, it also applies

${\frac {1}{3}}\zeta (2)=\sum _{k=1}^{\infty }{\frac {1}{k^{2}{2k \choose k}}},\,\,\,{\frac {17}{36}}\zeta (4)=\sum _{k=1}^{\infty }{\frac {1}{k^{4}{2k \choose k}}}.$

Series of this kind are also called Apéry series. In the desire to be able to apply Apéry's proof method to other zeta values if necessary, these are still the subject of intensive research today. Contributions were made by Ablinger, Bailey, Borwein, Sun and Zucker, among others. When attempting a generalisation, one naturally encounters connections to general harmonic sums and multiple polylogarithms. However, despite formulas such as

${\frac {1}{9}}\zeta (5)+{\frac {\pi ^{2}}{27}}\zeta (3)=\sum _{k=1}^{\infty }{\frac {H_{k}^{(3)}}{k^{2}{2k \choose k}}}$

the breakthrough has still not been achieved.

Linear independence over $\Q$

After all, it is known that infinitely many values $\zeta (2n+1)$ are irrational. More precisely, we can say that for every ε there is $\varepsilon >0$ $N\in {\mathbb {N}}$ , so that for all $n>N$

$\dim _{\mathbb {Q} }(\mathbb {Q} +\zeta (3)\mathbb {Q} +\zeta (5)\mathbb {Q} +\dotsb +\zeta (2n+1)\mathbb {Q} ))>{\frac {1-\varepsilon }{1+\log(2)}}\log(n)$

holds. From this inequality it follows that infinitely many values of the set $\{\zeta (2n+1)\mid n\in \mathbb {N} \}$ linearly independent over the body $\Q$ are. But this necessarily means that the values involved must all be irrational numbers. Vadim Zudilin was even able to show that at least one of the values $\zeta (5)$ , $\zeta (7)$ , $\zeta (9)$ and $\zeta (11)$ must be irrational.

Periods to ironstone series

Ramanujan gave the identity $\alpha \beta =\pi ^{2}$ for integers $N>0$ numbers α , β $\alpha ,\beta >0$ 2

${\begin{aligned}\alpha ^{-N}\left({\frac {1}{2}}\zeta (2N+1)+\sum _{k=1}^{\infty }{\frac {1}{k^{2N+1}(\mathrm {e} ^{2\alpha k}-1)}}\right)=&(-\beta )^{-N}\left({\frac {1}{2}}\zeta (2N+1)+\sum _{k=1}^{\infty }{\frac {1}{k^{2N+1}(\mathrm {e} ^{2\beta k}-1)}}\right)-\\&-2^{2N}\sum _{k=0}^{N+1}(-1)^{k}{\frac {B_{2k}}{(2k)!}}{\frac {B_{2N+2-2k}}{(2N+2-2k)!}}\alpha ^{N+1-k}\beta ^{k}\end{aligned}}$

an. The posterior polynomial in α $\alpha$ and β $\beta$ with rational coefficients is also called the Ramanujan polynomial. In a sense, this implies a closer relationship between the values $\zeta (2N+1)$ and π $\pi ^{2N+1}$ . By inserting special values, a rich abundance of explicit formulae can be found. For example, if one sets $N=1$ and α $\alpha =\beta =\pi$ , one obtains the series given by Matyáš Lerch around 1900

$\zeta (3)={\frac {7\pi ^{3}}{180}}-2\sum _{n=1}^{\infty }{\frac {1}{n^{3}(\mathrm {e} ^{2\pi n}-1)}}$

and more generally a representation that includes zeta values of even arguments:

$\zeta (4m-1)=-{\frac {1}{\pi }}\sum _{n=0}^{2m}(-1)^{n}\zeta (2n)\zeta (4m-2n)-2\sum _{n=1}^{\infty }{\frac {1}{n^{4m-1}(\mathrm {e} ^{2\pi n}-1)}}.$

Ramanujan's formula can be shown, for example, by applying the residue theorem to the function $f(z)=\cot(\pi z)\cot(\pi \mathrm {i} \alpha z)z^{-2N-1}$ However, it finds its deeper origin in the fact that the functions defined on the upper half plane are

$F_{2N+1}(z):=\sum _{n=1}^{\infty }{\frac {1}{n^{2N+1}}}{\frac {q^{n}}{1-q^{n}}},\,\,\,\,\,q:=\mathrm {e} ^{2\pi \mathrm {i} z}$

are just the Eichler integrals to Eisenstein series of weight $2N+2$ to the full moduli group. In particular, they have the transformation behaviour described by Ramanujan (for example, if one α $\alpha =-\pi iz$ with $\operatorname {Im} (z)>0$ the relation to the modular language becomes clearer) and the coefficients of the Ramanujan polynomial as well as the zeta values at odd places appear as so-called periods of the respective Eisenstein series. In 2011, Murty, Smyth and Wang showed that there is at least one algebraic number α $\alpha$ with $\operatorname {Im} (\alpha )>0,\,|\alpha |=1,\,\alpha ^{2N}\neq 1$ so that

${\frac {1}{2}}\zeta (2N+1)={\frac {F_{2N+1}(\alpha )-\alpha ^{2N}F_{2N+1}(-1/\alpha )}{\alpha ^{2N}-1}}.$

At the same time, however, they proved that the amount

$\left\{{\frac {F_{2N+1}(z)-z^{2N}F_{2k+1}(-1/z)}{z^{2k}-1}}\mid \operatorname {Im} (z)>0,z\in {\overline {\mathbb {Q} }},z^{2N}\neq 1\right\}$

contains at most one algebraic number, where ${\overline {\mathbb {Q} }}$ the algebraic closure of $\Q$ . It is still unclear whether one of the values $\pi ^{{2n+1}}$ can be represented $\zeta (2n+1)$ as a rational multiple of π However, many mathematicians consider this extremely unlikely. According to a conjecture by Kohnen, which was also formulated in 1989 in connection with periods of modular forms, all quotients $\zeta (2n+1)/\pi ^{2n+1}$ with are $n\geq 1$ transcendental numbers.

Numerical calculation

Especially for smaller values the Dirichlet series for the fast numerical calculation of the values is $\zeta (2n+1)$ not optimal. In the search for fast convergent series, Bailey made his mark by giving various BBP formulas. Examples of these exist for $\zeta (3)$ and $\zeta (5)$ . An example is the extremely fast convergent series

${\begin{aligned}\zeta (3)=&{\frac {5}{105}}\pi ^{2}\log(2)-{\frac {4}{105}}\log(2)^{3}+\\&+{\frac {4}{35}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left[{\frac {8}{(8k+1)^{3}}}-{\frac {4}{(8k+3)^{3}}}-{\frac {4}{(8k+4)^{3}}}-{\frac {2}{(8k+5)^{3}}}+{\frac {1}{(8k+7)^{3}}}+{\frac {1}{(8k+8)^{3}}}\right].\end{aligned}}$

Other fast convergent series, available for all values $\zeta (2n+1)$ , are from Wilton:

$\zeta (2n+1)=(-1)^{n-1}\pi ^{2n}\left({\frac {H_{2n+1}-\log(\pi )}{(2n+1)!}}+\sum _{k=1}^{n-1}{\frac {(-1)^{k}}{(2n-2k+1)!}}{\frac {\zeta (2k+1)}{\pi ^{2k}}}+\sum _{k=1}^{\infty }{\frac {(2k-1)!}{(2n+2k+1)!}}{\frac {\zeta (2k)}{\pi ^{2k}}}\right).$

Here $H_{n}$ denotes the th harmonic number. Note, however, that this is a recursive formula which requires precise knowledge of the values $\zeta (2k)$ (i.e. the Bernoulli numbers).

The decimal places of some values $\zeta (2n+1)$ shown in the following table.

2n + 1	ζ(2n + 1)	OEIS episode
3	1,2020569031595942853997381…	Episode A002117 in OEIS
5	1,0369277551433699263313654…	Episode A013663 in OEIS
7	1,0083492773819228268397975…	Episode A013665 in OEIS
9	1,0020083928260822144178527…	Episode A013667 in OEIS
11	1,0004941886041194645587022…	Episode A013669 in OEIS
13	1,0001227133475784891467518…	Episode A013671 in OEIS
15	1,0000305882363070204935517…	Episode A013673 in OEIS
17	1,0000076371976378997622736…	Episode A013675 in OEIS
19	1,0000019082127165539389256…	Episode A013677 in OEIS

Function values for non-positive integers

In contrast to the zeta values of positive whole arguments, about which almost nothing is known to date in the case of the odd values, the function values for non-positive integers are all known. It is known, for example, that they are all rational numbers. Like the zeta values of even positive numbers, they are very closely related to the Bernoulli numbers.

Via the integral formula derived with a Hankel contour

$\zeta (s)={\frac {\mathrm {e} ^{-\pi \mathrm {i} s}}{2\pi \mathrm {i} }}\Gamma (1-s)I(s)$

is deduced by inserting a non-positive integer $s=-n$ via the residue theorem:

$\zeta (-n)=-{\frac {B_{n+1}}{n+1}}.$

Here $B_{n}$ is the nth Bernoulli number. This can also be derived using Euler's formula for even function values and the functional equation (and vice versa).

Among other things, this gives $\zeta (-2n)=0$ for all

$\zeta (0)=-{\frac 12},\quad \zeta (-1)=-{\frac 1{12}},\quad \zeta (-3)={\frac 1{120}}.$

In his blog, mathematician Terence Tao goes into the "formulas"

$1+1+1+1+1+\cdots =-{\frac {1}{2}}$

$1+2+3+4+5+\cdots =-{\frac {1}{12}}$

$1+4+9+16+25+\cdots =0$

in detail. In particular, it explains that these equations make sense outside of the traditional calculation of infinite series and that the results to the right are even "uniquely determinable". Tao writes about this:

"Clearly, these formulae do not make sense if one stays within the traditional way to evaluate infinite series, and so it seems that one is forced to use the somewhat unintuitive analytic continuation interpretation of such sums to make these formulae rigorous."

"It is clear that these formulae make no sense if one stays within the traditional way of evaluating infinite series, and so it seems that one is forced to use the somewhat unintuitive interpretation by analytic continuation of such sums to make these formulae rigorous."

- Terence Tao

Function values for half-integer arguments

The following applies to the function values for half-integer arguments:

$\zeta ({\tfrac {1}{2}})=-1{,}46035\ 45088\ 09586\ 81288\ 94991\ldots$ (sequence A059750 in OEIS),

$\zeta ({\tfrac {3}{2}})=2{,}61237\ 53486\ 85488\ 34334\ 85675\ldots$ (sequence A078434 in OEIS).

$\zeta ({\tfrac {5}{2}})=1{,}34148\ 72572\ 50917\ 17975\ 67696\ldots$

$\zeta ({\tfrac {7}{2}})=1{,}12673\ 38673\ 17056\ 64642\ 78124\ldots$

Ramanujan gave in his diary the following series identity $\zeta (1/2)$ involving the value For positive real numbers α $\alpha ,\beta$ with αthe following applies $\alpha \beta =4\pi ^{3}$

$\sum _{n=1}^{\infty }{\frac {1}{\mathrm {e} ^{\alpha n^{2}}-1}}={\frac {\pi ^{2}}{6\alpha }}+{\frac {1}{4}}+{\frac {\sqrt {\beta }}{4\pi }}\left(\zeta \left({\frac {1}{2}}\right)+\sum _{n=1}^{\infty }{\frac {\cos({\sqrt {n\beta }})-\sin({\sqrt {n\beta }})-\mathrm {e} ^{-{\sqrt {n\beta }}}}{{\sqrt {n}}(\cosh({\sqrt {n\beta }})-\cos({\sqrt {n\beta }}))}}\right).$

This was taken up by some mathematicians and further generalised. For example, Kanemitsu, Tanigawa and Yoshimoto found similar identities involving the values $L(\chi ,a/b)$ for Dirichlet L-functions with odd and even

In 2017 Johann Franke gave the following identity for half-integer function values:

$A+B+C+D+E=\sum _{n=1}^{\infty }\left(\sum _{d|n}\sigma _{-3}(n/d)\sigma _{-3}(d)d^{-{\frac {1}{2}}}\right)\left(\mathrm {e} ^{-2\pi {\sqrt {n}}}-{\frac {1}{32}}\mathrm {e} ^{-8\pi {\sqrt {n}}}\right)$

with

$A={\frac {511}{92160}}\pi ^{2}\zeta ({\tfrac {3}{2}})\zeta ({\tfrac {9}{2}})$ , $B={\frac {1}{288}}\pi ^{3}\zeta ({\tfrac {3}{2}})\zeta ({\tfrac {5}{2}})$ , $C=-{\frac {7}{32}}\zeta ({\tfrac {3}{2}})\zeta ({\tfrac {5}{2}})\zeta (3)$ , $D={\frac {127}{11520}}\pi ^{3}\zeta ({\tfrac {1}{2}})\zeta ({\tfrac {7}{2}})$ and $E=-{\frac {31}{64}}\zeta ({\tfrac {1}{2}})\zeta ({\tfrac {7}{2}})\zeta (3)$ .

Here σ denotes $\sigma _{a}(n)$ the generalised divisor function. This identity is a special case of a very general framework that substantially extends Ramanujan series identities for L-functions.

Zeros

Trivial zeros

From the representation as an Euler product one can easily conclude that $\zeta (s)\neq 0$ for $\operatorname {Re} (s)>1$ holds. Together with the functional equation of the zeta function and the pole positions of the gamma function, it follows that the only zeros outside the critical strip $S=\{s\in \mathbb {C} \mid 0\leq \operatorname {Re} (s)\leq 1\}$ $-2,-4,-6,\dotsc$ are the "trivial" zeros These are all simple because for all $n \in \N$

$\zeta '(-2n)=(-1)^{n}{\frac {\zeta (2n+1)(2n)!}{2^{2n+1}\ \pi ^{2n}}}\not =0.$

Non-trivial zeros

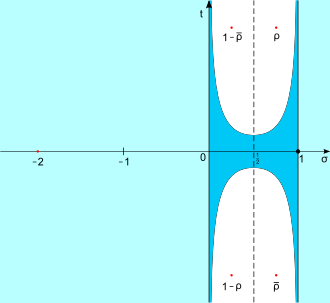
Besides the trivial zeros, the zeta function has further zeros in the critical strip $S=\{s\in \mathbb {C} \mid 0\leq \operatorname {Re} (s)\leq 1\}$ . These are also referred to as non-trivial zeros, since to date very little is known about their exact location. From their connection to Dirichlet's etafunction,

$\zeta (s)={\frac {\eta (s)}{1-2^{{1-s}}}},$

one can at least conclude that $\zeta (s)<0$ all real 0 ≤

Existence and asymptotic distribution

Due to the Euler product and the functional equation, all non-trivial zeros must lie within the closed critical strip $0\leq \operatorname {Re} (s)\leq 1$ lie, if they exist. Riemann was already aware that there are even infinitely many non-trivial zeros:

"The number of roots of $\Xi (t)=0$ whose real part lies between $0$ and is approximately $T/2\pi \log(T/2\pi )-T/2\pi$ because the integral extends $\int d\log \Xi (t)$ positively around the integral of the values of , whose imaginary part lies between $1/2\mathrm {i}$ and $-1/2\mathrm {i}$ whose real part lies between $0$ and is (except for a fraction of the order of the size $1/T$ ) is equal to $(T\log(T/2\pi )-T)\mathrm {i}$ ; but this integral is equal to the number of roots of $\Xi (t)=0$ lying in this area."

- Bernhard Riemann

Riemann thus gave a formula for the asymptotic distribution of non-trivial zeros for the first time in his work. He claimed that the number N(T) (calculated with multiplicity) of zeros within the rectangle $R=\{s\in \mathbb {C} \mid 0\leq \operatorname {Re} (s)\leq 1,0\leq \operatorname {Im} (s)\leq T\}$ satisfy the asymptotic equivalence

$N(T)\sim {\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}.$

He justified his train of thought (as briefly described above) via an evaluation of the zero-counting integral

$N(T)={\frac {1}{2\pi \mathrm {i} }}\int _{\partial R}{\frac {\xi '(s)}{\xi (s)}}\mathrm {d} s={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+O(\log T),$

where ξ $\xi (s)$ denotes the (somewhat differently scaled) Riemannian xi-function, which in particular has the same zeros in the critical strip as the zeta function. However, this statement was only rigorously proved by Mangoldt more than 50 years after Riemann's publication. The proof makes use of the functional equation ξ $\xi (1-s)=\xi (s)$ A standard proof given by Gérald Tenenbaum uses the extended rectangle $Q=\{-1\leq \operatorname {Re} (s)\leq 2,-T\leq \operatorname {Im} (s)\leq T\}$ and comes to

$2N(T)={\frac {1}{2\pi }}\operatorname {Im} \int _{\partial Q}{\frac {\xi '(s)}{\xi (s)}}\mathrm {d} s={\frac {2}{\pi }}\operatorname {Im} \int _{L}{\frac {\xi '(s)}{\xi (s)}}\mathrm {d} s,$

where because of all the symmetries of ξ can $\xi$ also $L=[2,2+\mathrm {i} T,1/2+\mathrm {i} T]$ be integrated over the line Using the simple formula for logarithmic derivatives, $\textstyle {\frac {(\prod _{k}f_{k})'}{\prod _{k}f_{k}}}=\sum _{k}{\frac {f_{k}'}{f_{k}}}$ and the fact, that imaginary parts of the logarithm are given by the argument, it follows that

$N(T)={\frac {1}{\pi }}[\operatorname {Arg} (\xi (s))]_{L}.$

While most of the factors of the ξ $\xi$ function in this formula are easy to evaluate and $T/2\pi \log(T/2\pi )-T/2\pi$ yield the magnitude , the most difficult part is estimating

$\operatorname {Im} \int _{L}{\frac {\zeta '(s)}{\zeta (s)}}\mathrm {d} s=O(\log(T)).$

The error $O(\log(T))$ could not be improved until today. Littlewood came up with the insight that the imaginary parts of the non-trivial zeros move closer and closer together. Thus, if one set γ $\gamma _{n}:=\operatorname {Im} (\rho _{n})$ (where ρ $\rho _{1},\rho _{2},\dots$ denotes the sequence of non-trivial zeros ascending by increasing positive imaginary parts), so $\textstyle \lim _{n\to \infty }\gamma _{n+1}-\gamma _{n}=0$ . This is concluded quite directly from the asymptotic equivalence

$\gamma _{n}\sim {\frac {2\pi n}{\log(n)}}.$

Symmetry properties

The functional equation of the zeta function and its basic mirror property with respect to conjugate arguments imply a pairwise occurrence of the non-trivial zeros. If, for example, ρ $\rho$ a zero in the critical strip, then due to the functional equation

$0=\Gamma \left({\frac {\rho }{2}}\right)\pi ^{{-\rho /2}}\zeta (\rho )=\Gamma \left({\frac {1-\rho }{2}}\right)\pi ^{{(\rho -1)/2}}\zeta (1-\rho )$

also $1-\rho$ zero. In addition, however, $0=\zeta (\rho )=\overline {\zeta (\overline {\rho })}$ , which is why also ρ $\overline {\rho }$ is zero; but analogously also $\overline {1-\rho }=1-\overline {\rho }.$ It should be noted that all values ρ $\rho ,1-\rho ,{\overline {\rho }}$ and lie in $1-\overline {\rho }$ the critical strip, can be connected there to form a rectangle and thus form a quasi-zero double pair.

However, if the Riemann conjecture is correct, all zeros lie on the straight line $\operatorname {Re} (s)=1/2$ where then ρ $\rho =1-\overline {\rho }$ oralways $\overline {\rho }=1-\rho$ holds.

Sums and series

The identity applies

$\sum _{\operatorname {Im} (\rho )>0}\left({\frac {1}{\rho }}+{\frac {1}{1-\rho }}\right)=1+{\frac {1}{2}}\gamma -{\frac {1}{2}}\log \left(4\pi \right).$

Here γ $\gamma$ the Euler-Mascheroni constant. However, the series over all does not converge $1/\rho$ absolutely. If one sums up the absolute amounts, one obtains

$\sum _{|\operatorname {Im} (\rho )|\leq T}{\frac {1}{|\rho |}}=O(\log(T)^{2}).$

This formula is required in deriving the explicit remainder estimates (also assuming the Riemann conjecture) of the prime number theorem.

Orders

Little is known about the order of the non-trivial zeros. It is assumed that all zeros of the zeta function have order 1. This assumption is supported by numerical investigations: So far, all zeros found were of first order.

However, J. B. Conrey, A. Ghosh and S. M. Gonek found statements under the assumption of the Riemann conjecture and the generalised Lindelöf conjecture. The latter states that for all ε $\varepsilon >0$ any Dirichlet character χ {\displaystyle $\chi$ q {\displaystyle the corresponding L-function for $1/2\leq \sigma \leq 1$ grows as follows

$L(\chi ,\sigma +\mathrm {i} t)=O((q(1+|t|))^{\varepsilon }).$

Assuming both, we obtain for the number of simple zeros $N_{s}(T)=\#\{\rho =\sigma +\mathrm {i} t\mid 0<\sigma <1,0\leq t\leq T,\zeta (\rho )=0,m(\rho )=1\}$ :

$\liminf _{T\to \infty }{\frac {N_{s}(T)}{N(T)}}\geq {\frac {19}{27}}.$

In 2013, H. M. Bui and D. R. Heath-Brown were able to show that this can essentially be proven without Lindelöf's conjecture. Furthermore, for values $T\gg H>0$

$\sum _{T<\operatorname {Im} (\rho )\leq T+H}\zeta '(\rho )={\frac {H}{4\pi }}\log(T)^{2}+O\left(H\log(T)+T^{{\frac {1}{2}}+\varepsilon }\right),$

where over zeros ρ $\rho$ is summed. So in every interval $[T,T+T^{{\frac {1}{2}}+\varepsilon }]$ lies the imaginary part of a simple zero.

According to a conjecture by Hardy and Littlewood, for every ε there exists $\varepsilon >0$ number T ( ε $T(\varepsilon )>0$ such that the function $\zeta ({\frac {1}{2}}+\mathrm {i} t)$ for all $T>T(\varepsilon )$ in the interval $[T,T+T^{{\frac {1}{4}}+\varepsilon }]$ has a zero of odd order. Moreover, there is a constant $c(\varepsilon )>0$ that

$N_{\mathrm {ungerade} }(T+T^{{\frac {1}{2}}+\varepsilon })-N_{\mathrm {ungerade} }(T)\geq cT^{{\frac {1}{2}}+\varepsilon }$

holds. Here $N_{\mathrm {ungerade} }(H)$ the number of zeros of odd order on $[0,H]$ .

In the case that all zeros should be simple, the non-vanishing values $\zeta '(\rho )$ come to mean something about the formula $x>1$ for non-natural

$\sum _{n\leq x}\mu (n)=\sum _{\rho }{\frac {x^{\rho }}{\rho \zeta '(\rho )}}-2-\sum _{n=1}^{\infty }\left({\frac {2\pi }{x}}\right)^{2n}{\frac {(-1)^{n}}{(2n)!n\zeta (2n+1)}}.$

Here μ $\mu (n)$ the Möbius function. However, this can only be shown under additional assumptions on the behaviour of the zeta function in the critical strip; this also refers to the intervals over which the partial zero-set sums are to be extended.

Zero-free regions

Already at the end of the 19th century it could be shown with the help of a simple proof of contradiction that the zeta function has no zeros on the straight line $\operatorname {Re}(s)=1$ . The basis of this proof is the inequality shown by Mertens, which is $\sigma >1$ for all $s=\sigma +\mathrm {i} t$ with σ

$\zeta (\sigma )^{3}\ |\zeta (\sigma +\mathrm {i} t)|^{4}\ |\zeta (\sigma +2\mathrm {i} t)|\ \geq 1.$

This zero-free region could then be enlarged further and further. Thus it was shown that a constant $C>0$ exists, so that ζ ( s $\zeta (s)$ no value s {\displaystyle

$\operatorname {Re} (s)>1-{\frac {C}{\max\{\log |\operatorname {Im} (s)|,1\}}}$

has a zero. Such improvements lead (in generalised form for Dirichlet L-functions), among other things, to the Siegel-Walfisz theorem.

The sharpest zero-free region to date, obtained with great technical effort, is given for $|\operatorname {Im} (s)|>3$ by

$\operatorname {Re} (s)\geq 1-{\frac {1}{57{,}54(\log {|\operatorname {Im} (s)|})^{\frac {2}{3}}(\log {\log {|\operatorname {Im} (s)}})^{\frac {1}{3}}}}.$

This leads to an improved error in the prime number theorem: For a constant

$\pi (x)=\operatorname {Li} (x)+O\left(x\exp(-c\log(x)^{\frac {3}{5}}\log(\log(x))^{-{\frac {1}{5}}})\right).$

An explicit value for the constant in the error function, namely $c=0{,}2098$ , was given by Ford in 2002. In particular, it is not known whether there is an ε $\varepsilon >0$ such that ζ ( s $\zeta (s)\neq 0$ for all s {\displaystyle

The Riemann conjecture

→ Main article: Riemann conjecture

Riemann conjectured in 1859 that all non-trivial zeros on the straight line $\{s\in \mathbb {C} \mid \operatorname {Re} (s)=1/2\}$ lie. Because of the functional equation, this is equivalent to $\zeta (s)\not =0$ for all This so-called Riemann conjecture has so far been neither proved nor disproved.

The location of the zeros in the critical strip is closely related to statements about the distribution of the prime numbers. For example, the statement that there are no zeros on the edge of the critical strip is a possible intermediate step in the proof of the prime number theorem. In other words, the zeros encode the deviation of the prime number function π $\pi (x)$ from the magnitude given by the prime number theorem $\operatorname {Li} (x)$ (integral logarithm). Their existence (guaranteed by the no longer convergent Euler product) is thus to be understood as a natural barrier that takes a certain fuzziness in the identification π $\pi (x)\approx \operatorname {Li} (x)$ a tribute. However, although this fuzziness is known to exist naturally, its intensity is not clarified and is related to the distribution of zeros. The closer zeros are to the straight line $\operatorname {Re}(s)=1$ , the greater the deviations will be. If $\zeta (s)\neq 0$ holds for all $\operatorname {Re} (s)>\beta$ 1 > $1>\beta \geq 1/2$ then for all ε $\varepsilon >0$

$\pi (x)=\operatorname {Li} (x)+O(x^{\beta +\varepsilon }).$

However, if all zeros lie on the mean straight line $\operatorname {Re} (s)=1/2$ , then this fuzziness is smallest possible (note that with ρ $\rho$ also $1-\rho$ is non-trivial zero). This would result in an astonishing smoothness in the distribution of the primes, for example, according to Lowell Schoenfeld, the following would then apply quite explicitly

$|\pi (x)-\operatorname {Li} (x)|\leq {\frac {x^{\frac {1}{2}}\log(x)}{8\pi }},\quad x\geq 2657.$

It should be noted that $x^{1/2}\log(x)$ becomes arbitrarily large, but asymptotically it is significantly smaller than $\operatorname {Li} (x)\sim x/\log(x)$

Atle Selberg gave the following assessment in 1946:

"I think the reason we believe so readily in the correctness of the Riemann conjecture is that it is the most beautiful and simplest distribution for the zeros that we can imagine. There is this symmetry along the critical straight lines. It would also result in the most natural distribution of primes. Somehow we would like to believe that at least something in this universe should be right."

- Atle Selberg, 1946

Results for the position on the critical straight line

In 1914 Godfrey Harold Hardy was able to show that infinitely many non-trivial zeros lie on the critical straight line $\operatorname {Re} (s)=1/2$ . In his then revolutionary proof, he made use of the fact that for all real number values the expression

$\textstyle \xi \left({\frac {1}{2}}+\mathrm {i} t\right)={\frac {1}{2}}\left({\frac {1}{2}}+\mathrm {i} t\right)\left(\mathrm {i} t-{\frac {1}{2}}\right)\pi ^{-1/4-\mathrm {i} t/2}\ \Gamma \left({\frac {1}{4}}+{\frac {\mathrm {i} t}{2}}\right)\zeta \left({\frac {1}{2}}+\mathrm {i} t\right)$

only assumes real function values. This simplified the problem to the existence of infinitely many zeros of a real-valued function to be solved. The proof by contradiction (see Reductio ad absurdum) shows that ξ $\xi \left(1/2+\mathrm {i} t\right)$ for $t\to \infty$ must change its sign infinitely often, which with the intermediate value theorem already shows that $\zeta (s)$ infinitely many zeros on $\operatorname {Re} (s)=1/2$ has.

In 1921 Hardy, together with his friend and colleague John Edensor Littlewood, improved the statement to the much stronger result that for sufficiently large values the number of zeros on the critical straight line in the segment is $\left\{1/2+\mathrm {i} t,0\leq t\leq T\right\}$ at least , where denotes a positive constant.

Atle Selberg improved this result in 1942 to $KT\log T$ and also showed that a positive proportion of all zeros lie on the critical straight line. Thus there is a constant $1\geq c>0$ so that

$N_{0}(T):=\#\{0\leq t\leq T\mid \zeta ({\tfrac {1}{2}}+\mathrm {i} t)=0\}\geq cN(T).$

For this and other contributions he was honoured with the Fields Medal in 1950. From this point on, work was done to find the highest possible values for

In the early 1970s Norman Levinson was able to show that at least one third ( $c>0{,}342$ non-trivial zeros must lie on the critical straight line, but T {\displaystyle assumed to sufficiently large. In 1989 Conrey improved this value to $c>2/5$ refining techniques from Levinson.

Numerical calculations

See also: Calculation of zeros of the Riemann zeta function

Early on, there were efforts to verify the Riemann conjecture and other phenomena by explicit numerical calculations. The methods improved explosively, especially in the age of powerful computers. So far, all non-trivial zeros found lie on the straight line $\operatorname {Re} (s)=1/2$ . However, since there are infinitely many non-trivial zeros, algorithms can at most be used to find a counterexample and not to prove the Riemann conjecture.

Numerical values of the early zeros

→ Main article: List of non-trivial zeros of the Riemann zeta function

The imaginary parts of the "first" zeros are for example

±k	±Im(ρk)	±k	±Im(ρk)
1	14,134725141734693790…	11	52,970321477714460644…
2	21,022039638771554993…	12	56,446247697063394804…
3	25,010857580145688763…	13	59,347044002602353079…
4	30,424876125859513210…	14	60,831778524609809844…
5	32,935061587739189690…	15	65,112544048081606660…
6	37,586178158825671257…	16	67,079810529494173714…
7	40,918719012147495187…	17	69,546401711173979252…
8	43,327073280914999519…	18	72,067157674481907582…
9	48,005150881167159727…	19	75,704690699083933168…
10	49,773832477672302181…	20	77,144840068874805372…

Nothing is known to date about the properties of these imaginary parts (irrationality, transcendence ...).

Hadamard product development

In addition to the Euler product, there is another product representation of the zeta function that for the first time directly includes its zeros in a possible definition. This is so significant because it is the key to the connection between prime numbers and zeros. Indeed, the decisive step in Bernhard Riemann's work was the "comparison" of these two products, which ultimately implies a close relationship between the product elements (in this case prime numbers and zeros). Because of its low convergence speed, however, the product representation is not suitable in practice as a basis for a numerical calculation algorithm for the zeta function.

Using Hadamard's product theorem for holomorphic functions, it is possible to reconstruct the zeta function using its zeros via a product. In doing so, it is exploited that the whole function ξ $\textstyle \xi (s)={\frac {1}{2}}s(s-1)\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)$ has the growth order 1. Accordingly, there are constants and such that

$\xi (s)=\mathrm {e} ^{as+b}\prod _{\rho }\left(1-{\frac {s}{\rho }}\right)\,\mathrm {e} ^{\frac {s}{\rho }}.$

Here $a=-1-{\frac {1}{2}}\gamma +{\frac {1}{2}}\log(4\pi )$ and $b=-\log(2)$ . This gives the Hadamard product, named after its discoverer Jacques Hadamard, which is global in ${\mathbb {C}}\setminus \{1\}$ converges:

$\zeta (s)={\frac {\mathrm {e} ^{(\log(2\pi )-1-{\frac {\gamma }{2}})s}}{2(s-1)\,\Gamma ({\tfrac {s}{2}}+1)}}\prod _{\rho }\left(1-{\frac {s}{\rho }}\right)\mathrm {e} ^{\frac {s}{\rho }}.$

A somewhat simpler (but only conditionally convergent) form of the Hadamard product is

$\zeta (s)={\frac {\pi ^{\frac {s}{2}}}{2(s-1)\Gamma ({\tfrac {s}{2}}+1)}}\prod _{\rho }\left(1-{\frac {s}{\rho }}\right).$

Absolute convergence results if the zeros are ordered "pairwise". Thus the factors $\textstyle \left(1-{\frac {s}{\rho }}\right)\left(1-{\frac {s}{1-\rho }}\right)$ under indexation $\operatorname {Im} (\rho )>0$ considered.

Atle Selberg

Jacques Salomon Hadamard

The real part of the function $\zeta (1/2+\mathrm {i} x)$ shown in blue and the imaginary part in red, so that one can clearly see the first non-trivial zeros

Besides the trivial zeros at $s=-2,-4,-6,\dotsc$ the Riemann zeta function also has non-trivial ones in the critical strip. Potential zero pairs are sporadically drawn in here: Due to the invariance of the functional equation over to 1-s and the mirroring of function values of complex conjugate arguments on the real axis, the pairs of zeros occur twice (i.e. mirrored) in each case. Only if the Riemann conjecture is correct do all horizontal pairs meet on the critical straight line σ $\sigma =1/2$ .

The first "trivial" zeros of the $\zeta$ function

"The function π $\pi (x)$ is, on a small scale, a staircase function of highly irregularity. On a large scale, however, it reveals one of the greatest mysteries that mathematics offers through an amazing smoothness (see picture)." (J. Neukirch)

Other properties in the critical strip

Voronin's universality theorem

According to Voronin's universality theorem, the Riemann $\zeta$ -function is able to approximate any holomorphic function in a zero-free circular disk with radius 1/4 arbitrarily exactly.

As an illustrative comparison, imagine that for every holomorphic function there is a kind of "map" that represents the heights and depths as well as the compass direction of the function values in the complex plane. The universality theorem now states that if one were to scan the map of the zeta function in a certain infinite area, sooner or later one would come across areas that arbitrarily resemble sections of the maps of other functions, i.e. together with all the "mountains" and "valleys" entered in them. The only prerequisite here, however, is that the value 0 is never entered on the map section of the foreign function.

Formally expressed: Let be a compact subset of the strip $S:=\{s\in \mathbb {C} \mid 1/2<\operatorname {Re} (s)<1\}$ connected complement. Now let $f\colon U\to {\mathbb {C}}$ a continuous function which is holomorphic inside and $s\in U$ vanishes for no Then for every ε there exists $\varepsilon >0$ $t\geq 0$ so that

$|\zeta (s+\mathrm {i} t)-f(s)|<\varepsilon$

for all $s\in U$ . Note here that in general it is only an approximation, so ε $\varepsilon >0$ must be guaranteed. If one had $\zeta (s+\mathrm {i} t)=f(s)$ for a subset $M\subset U$ with cluster point in the interior of then by the identity theorem for holomorphic functions it already followed $\zeta (s+\mathrm {i} t)=f(s)$ on the whole of .

Even more is true: the lower asymptotic density of all satisfying an approximation is positive, as shown by the inequality

$0<\liminf _{T\to \infty }{\frac {1}{T}}\,\lambda \ \left(\left\{t\in [0,T]\mid \max _{s\in U}\left|\zeta (s+\mathrm {i} t)-f(s)\right|<\varepsilon \right\}\right)$

proves. Here λ is $\lambda$ the standard Lebesgue measure on the real numbers. For very small circular disks, even effective bounds can be given if satisfies certain conditions. Thus, for all in $|s|\leq 0{,}05$ analytic with $\textstyle \max _{|s|\leq 0{,}05}|f(s)|\leq 1$ and $0<\varepsilon <1/2$ 0 ≤ τ ≤ $0\leq \tau \leq \exp(\exp(10\varepsilon ^{-13}))$ so that

$\max _{|s|\leq 0{,}0001}\left|\log \zeta \left(s+{\frac {3}{4}}+\tau \mathrm {i} \right)-f(s)\right|<\varepsilon .$

A similar result is found for the lower asymptotic density. Note that in this version the modified function $\log \zeta (s)$ is universal.

This astonishing property entails some consequences. For example, it can be shown that the Riemann zeta function does not obey any algebraic differential equation. More precisely, one can show that if $\Phi \colon \mathbb {C} ^{N}\to \mathbb {C}$ a continuous function, $h_{1},\dotsc ,h_{n}$ constants, $k_{1},\dotsc ,k_{n}$ natural numbers with $N=k_{1}+\dotsb +k_{n}$ such that

$\Phi \left(\zeta (s+h_{1}),\zeta '(s+h_{1}),\dotsc ,\zeta ^{(k_{1}-1)}(s+h_{1}),\zeta (s+h_{2}),\dotsc ,\zeta ^{(k_{2}-1)}(s+h_{2}),\dotsc \right)=0,$

then it already follows $\Phi =0$ . Moreover, if $n,s\in \mathbb {C}$ with $1/2<\operatorname {Re} (s)<1$ chosen arbitrarily, it follows that the quantity

$\{(\zeta (s+\mathrm {i} t),\zeta '(s+\mathrm {i} t),\dotsc ,\zeta ^{(n-1)}(s+\mathrm {i} t))\mid t\in \mathbb {R} \}$

always dense in $\mathbb {C} ^{n}$ lies.

Approximate functional equation

Although the Dirichlet series no longer converges in the critical strip, its partial sums can lead to a good approximation of the zeta functions. A very simple formula of this type, valid for $\operatorname {Re} (s)>0$ , for example, is

$\zeta (s)=\sum _{n\leq N}{\frac {1}{n^{s}}}+{\frac {N^{1-s}}{s-1}}+O\left(\left(1+{\frac {|s|}{\operatorname {Re} (s)}}\right)N^{-\operatorname {Re} (s)}\right).$

For fixed values the error becomes small for sufficiently large values However, |s| is a severe disadvantage for large imaginary parts. To counteract this, σ chosen $\sigma _{0}>0$ With the aid of the van der Corputs summation formula, for $|\operatorname {Im} (s)|\leq 4x$ the remainder element can be further improved to

$\zeta (s)=\sum _{n\leq x}{\frac {1}{n^{s}}}-{\frac {x^{1-s}}{1-s}}+O(x^{-\operatorname {Re} (s)}),\qquad \operatorname {Re} (s)\geq \sigma _{0},$

by adapting the summation range to the argument. Thus the zeta function in by the first | $0 < \operatorname{Re}(s) < 1$ $|\operatorname {Im} (s)|$ approximate members of the Dirichlet series. In the range the following representation by a Dirichlet series $\operatorname {Re} (s)<0$ follows by means of the functional equation:

$\zeta (s)={\frac {(2\pi )^{s}}{2\cos \left({\frac {\pi s}{2}}\right)\Gamma (s)}}\sum _{n=1}^{\infty }n^{s-1}.$

Again, a corresponding approximation in the critical strip is to be expected and combining both results, with $s=\sigma +\mathrm {i} t$ and $2\pi xy=|t|$ , $x,y\geq 1$ the formula

$\zeta (s)=\sum _{n\leq x}{\frac {1}{n^{s}}}+{\frac {(2\pi )^{s}}{2\cos \left({\frac {\pi s}{2}}\right)\Gamma (s)}}\sum _{n\leq y}{\frac {1}{n^{1-s}}}+O((x^{-\sigma }+|t|^{{\frac {1}{2}}-\sigma }y^{\sigma -1})\log |t|),$

which is also called Approximate functional equation. This was discovered in 1921 by Hardy and Littlewood, but as it turned out later, it was already known to Bernhard Riemann. It is a powerful tool for investigating the zeta function in the critical strip.

Growth in the critical strip

Known results

With the approximate functional equation it follows via $x=y={\sqrt {|t|/2\pi }}$

$\zeta (\sigma +\mathrm {i} t)=O\left(|t|^{{\frac {1}{2}}(1-\sigma )}\log |t|\right).$

In 1958, Korobov and Vinogradov estimated the

$\zeta (\sigma +\mathrm {i} t)=O\left((1+t^{B(1-\sigma )^{3/2}})(\log(t))^{\frac {2}{3}}\right),\qquad \sigma \geq 0,\,\,t\geq 2,$

with a $B>0$ . For the straight line $\operatorname {Re}(s)=1$ they thus showed

$\zeta (1+\mathrm {i} t)=O\left(\log(t)^{\frac {2}{3}}\right),\qquad t\geq 2.$

Richert gave a more explicit form in 1967:

$|\zeta (\sigma +\mathrm {i} t)|\leq A|t|^{100(1-\sigma )^{\frac {3}{2}}}\log(t)^{\frac {2}{3}},\qquad \sigma \geq {\frac {1}{2}},\,\,t\geq 3.$

From these results, the largest known zero-free region of $\zeta (s)$ determined. Within this area the estimates

${\frac {\zeta '(\sigma +\mathrm {i} t)}{\zeta (\sigma +\mathrm {i} t)}}=O\left(\log(t)^{\frac {2}{3}}\log(\log(t))^{\frac {1}{3}}\right)$

${\frac {1}{\zeta (\sigma +\mathrm {i} t)}}=O\left(\log(t)^{\frac {2}{3}}\log(\log(t))^{\frac {1}{3}}\right)$

and

$|\log \zeta (\sigma +\mathrm {i} t)|\leq {\frac {2}{3}}\log(\log(t))+{\frac {1}{3}}\log(\log(\log(t)))+O(1).$

The Lindelöf presumption

→ Main article: Lindelöf's conjecture

For all real σ the size is $\sigma$

$\mu (\sigma )=\inf _{c\in \mathbb {R} }\{c:|\zeta (\sigma +\mathrm {i} t)|\ll |t|^{c}\}=\limsup _{t\to \infty }{\frac {\log |\zeta (\sigma +\mathrm {i} t)|}{\log t}}$

finite. The notation μ $\mu$ is historically conditioned. It is a measure of how fast the Riemann zeta function grows along vertical straight lines. For real numbers outside the critical strip $0<\sigma <1$ ( σ ) {\displaystylecalculated. For $\mu (\sigma )$ σ $\sigma >1$ ( σ $\mu (\sigma )=0$ since for all values with $\operatorname {Re} (s)>1$ after estimation of the sum by means of absolute convergence | $|\zeta (s)|\leq \zeta (\operatorname {Re} (s))$ follows, one obtains μ $\mu (\sigma )\leq 0$ . On the other hand, via the Möbius function, the lower bound $0<\zeta (\operatorname {Re} (2s))/\zeta (\operatorname {Re} (s))\leq |\zeta (s)|$ , which is why simultaneously μ $\mu (\sigma )\geq 0$ and thus μ $\mu (\sigma )=0$ is proved. Together with this result it follows via Stirling's formula and the functional equation of the zeta function μ $\mu (\sigma )=1/2-\sigma$ for all σ Also secured are the boundary values μ $\mu (0)=1/2$ and μ $\mu (1)=0$ .

The exact values of μ $\mu (\sigma )$ for critical values $0<\sigma <1$ unknown today (December 2019). The culprit is that size characterisations of this precision are very difficult and sometimes impossible without absolute convergence. It is believed that the zeta function ${\tfrac {1}{2}}\leq \sigma <1$ continues to grow slowly in the vertical regions to , so μ ( σ $\mu (\sigma )=0$ but is no longer necessarily constrained by a constant. This is equivalent to $|\zeta (\sigma +\mathrm {i} t)|=O(t^{\varepsilon })$ for all ε This statement is also called Lindelöf's conjecture (after Ernst Leonard Lindelöf) and is still unproven today. However, it is known that the function $\sigma \leq 1$ unbounded $|\zeta (s)|$ on any vertical straight line σ $\sigma +\mathrm {i} t$ with σ

Nevertheless, one can $\mu$ give estimates for the behaviour of μ Via the approximate functional equation, one concludes, for example

$\mu (\sigma )\leq {\frac {1}{2}}(1-\sigma ),\qquad 0<\sigma <1.$

One can also show that μ $\mu(\sigma)$ is convex and that the following downward estimate holds:

$\mu (\sigma )\geq \max(0,{\tfrac {1}{2}}-\sigma ).$

Lindelöf's conjecture is equivalent to the fact that equality always holds in the last inequality. Because of the convexity of μ $\mu(\sigma)$ and the functional equation of the zeta function, this is already equivalent to μ $\mu (1/2)=0$ .

Relationship to moments of power

The number-theoretical significance of Lindelöf's conjecture becomes apparent through a connection to the power moments of the zeta function along the critical straight line. If one defines

$I_{k}(T):=\int \limits _{0}^{T}\left|\zeta \left({\tfrac {1}{2}}+\mathrm {i} t\right)\right|^{2k}\mathrm {d} t,$

then it is equivalent to the statement $I_{k}(T)=O(T^{1+\varepsilon })$ for all values $k=1,2,3,\dotsc$ . The power moments appear, among other things, in error estimates in the Dirichlet divisor problem and in statistics. Explicitly applies

$I_{1}(T)=T\log(T)+O(T)$

and Heath-Brown showed in 1979

$I_{2}(T)=T\sum _{k=0}^{4}c_{k}\log(T)^{4-k}+O\left(T^{{\frac {7}{8}}+\varepsilon }\right),$

with $c_{0}=1/(2\pi ^{2})$ and computable c_k . The moments of the zeta function are, especially for large values (where the theory is much more difficult), a highly topical area of research. Contributions were made by Conrey, Gonek for large values and Heath-Brown for rational In connection with the theory of random matrices, Keating and Snaith formulated a conjecture about the exact asymptotic behaviour of power moments.

Connection with the Riemann conjecture

There is a relationship between the growth of an analytic function and the number of its zeros because of Jens' formula. In fact, Lindelöf's conjecture holds exactly if for all holds: $\operatorname {Re} (s)>1/2$

$\lim _{T\to \infty }{\frac {\#\{w\in \mathbb {C} \mid \zeta (w)=0,T-1<\operatorname {Im} (w)<T+1,\operatorname {Re} (w)>\operatorname {Re} (s)\}}{\log T}}=0.$

This was first proved by Backlund in 1918. If the Riemann conjecture is correct, the numerator would always be 0, with which the Lindelöf conjecture follows directly. However, the validity of the Riemann conjecture cannot be deduced from the Lindelöf conjecture, since a single non-trivial zero with a real part unequal to 1/2 sufficient to refute the latter.

In the event that the Riemann conjecture is true, Littlewood showed

$\zeta ({\tfrac {1}{2}}+\mathrm {i} t)=O\left(\exp \left(C{\frac {\log(t)}{\log(\log(t))}}\right)\right)$

with a positive constant Soundararajan showed that can be set. $C=3/8$

Study on quantum optical methods

The course of the zeta function in the complex plane, especially along stripes running parallel to the imaginary axis, is also specifically investigated experimentally with quantum optical methods in the 2000s, namely with interference methods analogous to holography, because of the connection with the prime number distribution and the so-called factorisation problem directly affected by it. For this purpose, one divides the defining sum into two parts with positive and negative phase, ψ $\psi$ and ψ $\psi ^{*}$ which are then brought to interference.

The course of the (Lindelöfian) μ $\mu$ -function is $x>1$ < 0 The red gradient is assumed in the real critical strip. It is known that μ $\mu$ smaller there than the blue curve.

Any holomorphic function defined on the critical strip and zero-free in a domain is approximated arbitrarily exactly

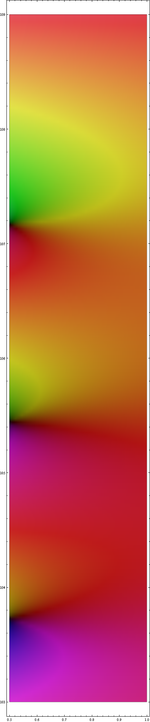
Complex diagram with colouring of the function values: The zeta function behaves very chaotically in the critical strip. Here is a section for
$1/2<\operatorname {Re} (s)<1,$
$103<\operatorname {Im} (s)<109.$

Ernst Lindelöf

Application in analytic number theory

Relationship to the prime number distribution

The prime number theorem

→ Main article: Prime number set

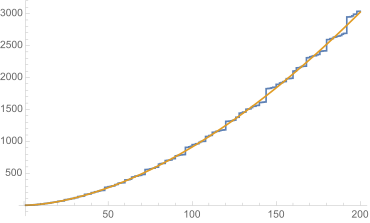
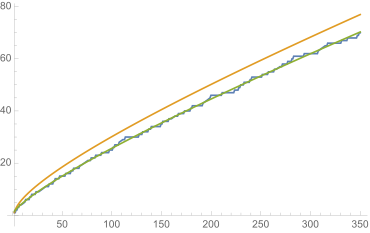
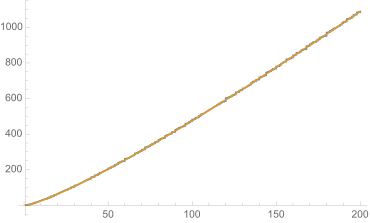
As the 15-year-old Gauss already suspected, the number of all primes π $\pi (x)$ under a given bound grows asymptotically equal to the expression $x/\log(x)$ . Thus it holds:

$\lim _{x\to \infty }{\frac {\pi (x)}{x/\log(x)}}=1.$

However, this so-called prime number theorem was not proved independently by Hadamard and Poussin until a hundred years later. For a proof, the identity valid between the Riemann zeta function and the prime function can be used.

$P(s)=\sum _{p\ {\text{Primzahl}}}{\frac {1}{p^{s}}}=\log \zeta (s)+\sum _{n=2}^{\infty }{\frac {\mu (n)}{n}}\log \zeta (ns)$

which finds its origin in the Euler product. If we now know that $\zeta (s)\neq 0$ for all $\operatorname {Re} (s)\geq 1$ follows that P(s) refers to the straight line segment can be $\{\operatorname {Re} (s)=1\}\setminus \{1\}$ holomorphically continued and written in an environment of s=1 in the form $P(s)=-\log(s-1)+g(s)$ with a holomorphic function With Delange's dew theorem it thus already follows that

$\sum _{p\leq x \atop p\ {\text{Primzahl}}}1=\pi (x)\sim {\frac {x}{\log(x)}}\sim \operatorname {Li} (x).$

Here denotes $\operatorname {Li} (x)$ the integral logarithm. Another more elementary approach uses the Mangoldt function and the Wiener-Ikehara dove theorem. A "fast" method comes from Donald Newman and uses the Möbius function. This was further shortened by Don Zagier in 1997.

Explicit calculation of the prime number function

From the unconditional convergence of the Euler product it follows immediately that $\zeta (s)$ on the half-plane $\{s\in \mathbb {C} \mid \operatorname {Re} (s)>1\}$ has no zeros. Furthermore, the identity holds there, $\textstyle \log \zeta (s)=\sum _{p\ {\text{Primzahl}}}\sum _{n=1}^{\infty }{\frac {1}{np^{ns}}},$ from which Riemann finally deduces that for all $c>1$ which is very important from the point of view of number theory.

$\Pi (x):=\sum _{p^{n}<x}{\frac {1}{n}}={\frac {1}{2\pi \mathrm {i} }}\int \limits _{c-\mathrm {i} \infty }^{c+\mathrm {i} \infty }{\frac {\log \zeta (s)}{s}}x^{s}\mathrm {d} s$

by means of an inverse Mellin transformation. The sum on the left-hand side yields for each prime power $p^{n}<x$ contribution 1 / n 1/n , can thus be $\textstyle \pi (x)+{\frac {1}{2}}\pi (x^{1/2})+{\frac {1}{3}}\pi (x^{1/3})+\dotsb$ identified with π . Here π $\pi (x)$ denotes the prime function that counts how many primes are smaller than Riemann calculated the right integral by means of a precursor of the Hadamard product and thus found the explicit formula $x>1$ non-integers

$\Pi (x)=\operatorname {Li} (x)-\sum _{\rho }\operatorname {Li} (x^{\rho })-\log 2+\int \limits _{x}^{\infty }{\frac {\mathrm {d} t}{t(t^{2}-1)\log t}},$

where $\operatorname {Li} (x)$ denotes the integral logarithm. Via Möbius-inversion, $\textstyle \Pi (x)=\pi (x)+{\frac {1}{2}}\pi (x^{1/2})+{\frac {1}{3}}\pi (x^{1/3})+\dotsb$ the value π $\pi (x)$ can be reconstructed:

$\pi (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi (x^{1/n})=\Pi (x)-{\frac {1}{2}}\Pi (x^{1/2})-{\frac {1}{3}}\Pi (x^{1/3})\pm \dotsb .$

Here μ $\mu (n)$ the Möbius function. Via the non-trivial zeros, the value of the prime number function π $\pi (x)$ at the position can thus be calculated exactly. In particular, a complete error correction of the prime number theorem is possible. Regarding convergence, it should be noted that the sum over ρ $\rho$ adds the zeros in pairs after their conjugation. Furthermore, the terms in the sum are to be understood as $\operatorname {Li} (x^{\rho })=\operatorname {Ei} (\rho \log x)$ (here denotes $\operatorname {Ei}$ the (complex) integral exponential function), because: Confusion can arise when evaluating $x^{{\rho }}$ over the main branch of the complex logarithm.

Riemann interpreted the "real principal part" of his formula as a better approximation than $\operatorname {Li} (x)$ to π $\pi(x)$ . He also highlighted the possible importance of zeros ("periodic links") in deciphering the irregular distances between primes:

"The well-known approximation formula π $\pi (x)=\operatorname {Li} (x)$ is therefore only correct up to quantities of the order $x^{\frac {1}{2}}$ and gives a somewhat too great value; for the non-periodic members in the expression of $\operatorname {Li} (x)$ are, apart from quantities which do not grow to infinity with $\textstyle \operatorname {Li} (x)-{\frac {1}{2}}\operatorname {Li} (x^{\frac {1}{2}})-{\frac {1}{3}}\operatorname {Li} (x^{\frac {1}{3}})-{\frac {1}{5}}\operatorname {Li} (x^{\frac {1}{5}})+{\frac {1}{6}}\operatorname {Li} (x^{\frac {1}{6}})-{\frac {1}{7}}\operatorname {Li} (x^{\frac {1}{7}})+\cdots$ . In fact, the comparison of $\operatorname {Li} (x)$ with the number of prime numbers under carried out by Gauss and Goldschmidt and continued up to = three million has always shown this number to be smaller than $\operatorname {Li} (x)$ from the first hundred thousand onwards, and indeed the difference grows under some fluctuations gradually with . But also the local condensation and dilution of the prime numbers, which depends on the periodic members, has already attracted attention in the counts, without, however, a regularity being noticed in this. In a possible new count, it would be interesting to follow the influence of the individual periodic elements contained in the expression for the density of the primes.

- Bernhard Riemann

The function addressed by Riemann

$R(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {Li} (x^{\frac {1}{n}})=1+\sum _{k=1}^{\infty }{\frac {\log(x)^{k}}{kk!\zeta (k+1)}}$

is nowadays called the Riemann R-function and for the first values gives a (in places clearly) better approximation of π $\pi (x)$ than $\operatorname {Li} (x)$ . However, since Littlewood could show that the function π $\pi (x)-\operatorname {Li} (x)$ has infinitely many zeros, this cannot be the case for all Only conceivable would be an "average" better approximation in the sense of

$\int \limits _{2}^{x}\left|\pi (t)-R(t)\right|\mathrm {d} t<\int \limits _{2}^{x}\left|\pi (t)-\operatorname {Li} (t)\right|\mathrm {d} t$

for all (sufficiently large) , but this is still unknown today.

The Selberg-Delange Method

→ Main article: Selberg-Delange method

The Selberg-Delange method is a technique to determine the mean order of a number theoretic function as long as its generated Dirichlet series has sufficiently good properties. Here, one makes use of complex powers of the zeta function. For $z \in \mathbb{C}$ one considers $\zeta (s)^{z}$ and finds with the Euler product for all

$\zeta (s)^{z}=\prod _{p\ {\text{Primzahl}}}\left(1+\sum _{v=1}^{\infty }{z+v-1 \choose v}p^{-sv}\right).$

Let $F(s)=\sum a(n)/n^{s}$ be a Dirichlet series converging on the half-plane $\operatorname {Re} (s)>1$ . If for a $z\in \mathbb {C}$ the function $G(s)=F(s)\zeta (s)^{-z}$ can be holomorphically $\zeta (s)$ continued into a zero-free region of and has a well-controlled growth there, the sum

$\sum _{n\leq x}a(n)$

can be estimated explicitly. The error depends on the size of the zero-free area of $\zeta (s)$ An advantage of this method is that, apart from convergence of the series, no essential conditions $a(n)$ are imposed on the terms disadvantage is the necessary growth condition on the function $G(s)$ .

An application example of the Selberg-Delange method is a result by Paul Bateman concerning Euler's phi function. This states that the number of natural numbers for which φ $\varphi (n)\leq x$ holds, is asymptotically given by

${\frac {\zeta (2)\zeta (3)}{\zeta (6)}}x+O\left(x\mathrm {e} ^{-c{\sqrt {\log(x)}}}\right)$

where $c>0$ constant. The Dirichlet series considered for this has the form for $\operatorname {Re} (s)>1$ form

$\sum _{m=1}^{\infty }{\frac {1}{\varphi (m)^{s}}}=\zeta (s)\prod _{p\ \mathrm {Primzahl} }\left(1+{\frac {1}{(p-1)^{s}}}-{\frac {1}{p^{s}}}\right).$

The Dirichlet divider problem

→ Main article: Dirichletian divisor problem

Lindelöf's conjecture is already a number-theoretic statement. It can be used to describe the nature of divisor sums in quite some detail. These sums are the subject of Dirichlet's divisor problem, which, in the classical variant, searches for the magnitude of the sum

$\sum _{n\leq x}d(n)$

where d(n) denotes the number of positive divisors of example, $d(6)=4$ since 6 has the divisors 1,2,3 and 6. Peter Gustav Lejeune Dirichlet already showed:

$\sum _{n\leq x}d(n)=x\log(x)+(2\gamma -1)x+O(x^{\beta }),$

with β $\beta \leq {\tfrac {1}{2}}$ . The divisor problem now asks about the nature of the numbers β $\beta$ which may be substituted into this equation. In 1922, J. van der Corput showed β $\beta \leq {\tfrac {33}{100}}$ and the estimate β $\beta \leq {\tfrac {131}{416}}$ was given by M. N. Huxley in 2003. On the other hand, G. H. Hardy and E. Landau that βmust hold. $\beta \geq {\tfrac 14}$

This problem can even be generalised. For this one defines

$d_{k}(n):=\sum _{u_{1},\dotsc ,u_{k} \atop u_{1}\cdots u_{k}=n}1.$

While $d_{2}(n)=d(n)$ and counts all pairs $(u_{1},u_{2})$ with $u_{1}u_{2}=n$ (in other words the divisors of ), counts $d_{k}(n)$ all tuples $(u_{1},\dots ,u_{k})$ with $u_{1}\cdots u_{k}=n$ .

With the help of the power moments of the Riemann zeta function, the general statement

$\sum _{n\leq x}d_{k}(n)=xP_{k}(\log x)+O(x^{1-{\frac {2}{k+4}}+\varepsilon })$

can be taken. The term $xP_{k}(\log x)$ is given by the residual of the function $\zeta (s)^{k}x^{s}/s$ at position 1. The background of this connection is that the Dirichlet series of the function $d_{k}(n)$ generated $\zeta (s)^{k}$ by the But if Lindelöf's conjecture is true, and only then, this error can be replaced for all $k\geq 2$ by $O(x^{1/2+\varepsilon })$ for all ε $\varepsilon >0$ From $I_{2}(T)=TP(\log T)+O(T^{7/8+\varepsilon })$ with a polynomial the fourth degree follows, for example, $A_{4}(x)=xP_{4}(\log x)+O(x^{1/2+\varepsilon }).$

Product compositions

A product composition of the natural number is of the form $n=n_{1}\cdots n_{k}$ with natural numbers $n_{j}\geq 2$ . If denotes $M(n)$ the number of all product compositions (the order of the factors plays a role) of then for numbers with a sufficiently large real part, if one $M(1):=1$ requires

${\frac {1}{2-\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {M(n)}{n^{s}}}.$

This was used by László Kalmár to develop the following asymptotic formula $\textstyle \alpha <{\frac {1}{2(\kappa -1)\log(2)}}$ for any α

$\sum _{n\leq x}M(n)=-{\frac {x^{\kappa }}{\kappa \zeta '(\kappa )}}+O\left(x^{\kappa }\log(x)^{-\alpha \log(\log(\log(x)))}\right)\approx 0{,}31817x^{1{,}72867}.$

Here κ $\kappa \approx 1{,}728647$ is the unique solution of the equation $\zeta (x)=2$ in the interval $]1,\infty [$ . This is nowadays also called Kalmár's composition constant. Kalmár himself gave the estimate In the meantime, the results have been further refined.

Determination of the mean order of number theoretic functions via Dewer theorems

→ Main article: Wiener-Ikehara Theorem

Dew theorems for Dirichlet series $\textstyle \sum a(n)/n^{s}$ with $a(n)\geq 0$ already apply under quite weak conditions. Thus, growth formulas for summatorial functions can be

$A(x):=\sum _{n\leq x}a(n)$

already deduce that the associated Dirichlet series on a half-plane $\operatorname {Re} (s)>\sigma _{0}>0$ have $\sigma _{0}$ singular point at the point σ 0 {\displaystyle \sigma(ie, that the holomorphic function represented by the Dirichlet series for no open set σ $\sigma _{0}\in U$ holomorphizes to ) and otherwise can be $U\cup \{s\in \mathbb {C} \mid \operatorname {Re} (s)>\sigma _{0}\}$ holomorphically from the right onto the straight line Re $\operatorname {Re} (s)=\sigma _{0}$ can be continued. Compositions of Riemann zeta functions very often fulfil these conditions.

Thus it follows from $\textstyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a)$ for real-valued already a>0

$\sum _{n\leq x}\sigma _{a}(n)\sim {\frac {\zeta (a+1)}{a+1}}x^{a+1}.$

For the phi function, $\textstyle \sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}$

$\sum _{n\leq x}\varphi (n)\sim {\frac {3}{\pi ^{2}}}x^{2}.$

A good tool for deriving these identities is Delange's Taubersatz. In the case that the considered number theoretic function is just indicator function of a subset $A\subset \mathbb {N}$ , dew theorems provide information about its asymptotic density. The prime number theorem, which covers the case $A=\mathbb {P}$ (set of prime numbers) is such a poet's theorem.

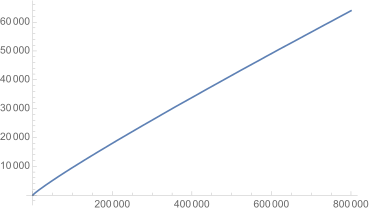
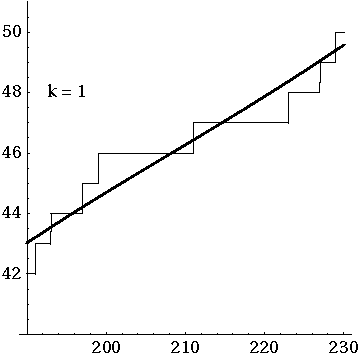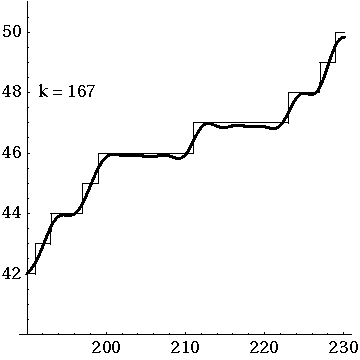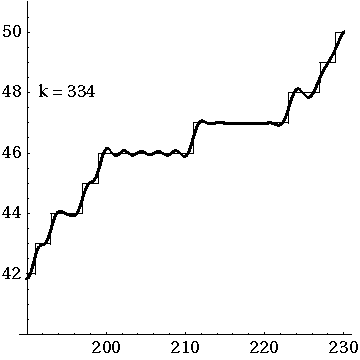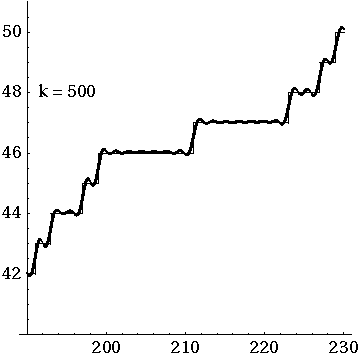
Approximation of the prime function in the interval $[200,230]$ by the first 500 zeros. The index in this animation stands for the number of pairs of zeros used in the above sum.

The step function $\textstyle s(x)=\sum _{n\leq x}M(n)$ is $\textstyle f(x)=0{,}31817x^{1{,}72867}$ approximated by the function

Over long distances the function $\operatorname {Li} (x)$ (orange) above the staircase function π $\pi (x)$ (blue). However, according to a paper by Littlewood, infinitely many intersections take place. The Riemann function $R(x)$ (green) is a much better approximation, at least for small values.

The staircase function $\textstyle s(x)=\sum _{n\leq x}d(n)$ is $\textstyle f(x)=x\log(x)+(2\gamma -1)x$ approximated by the function

Application in algebraic number theory and generalisations

Dirichlet L-functions

→ Main article: Dirichlet L-function

The Riemann zeta function is a special Dirichlet L-function. It corresponds to the so-called trivial character χ $\chi (n)=1$ for all values . For this reason, it is the central subject of algebraic number theory, which deals with the structure of characters to certain groups.

Relationship to the Dedekind zeta function of number fields

→ Main article: Dedekind zeta function

The Dedekind zeta function $\zeta _{K}(s)$ of a number field generalises the Riemann zeta function. Thereby $\zeta _{K}(s)$ deals with the "prime factorization" in the integer ring ${\mathcal {O}}_{K}$ of . The ring $\mathcal{O}_K$ is the set of all elements $x\in K$ which are solutions of a polynomial equation $x^{n}+a_{n-1}x^{n-1}+\cdots +a_{0}=0$ with integers $a_{n-1},\dots ,a_{0}$ For example, ${\mathcal {O}}_{\mathbb {Q} }=\mathbb {Z}$ and ${\mathcal {O}}_{\mathbb {Q} ({\sqrt {-5}})}=\mathbb {Z} +\mathbb {Z} {\sqrt {-5}}$ . The question whether there is in general a unique decomposition into prime elements in ${\mathcal {O}}_{K}$ is of number theoretic relevance and its answer is in general "no". Thus, $3,7,1\pm 2{\sqrt {-5}}$ although the numbers are all prime and pairwise distinct in $\mathbb {Z} +\mathbb {Z} {\sqrt {-5}}$ but the following holds

$21=3\cdot 7=(1+2{\sqrt {-5}})\cdot (1-2{\sqrt {-5}}).$

In order to re-establish uniqueness, the transition is made to the ideals of ${\mathcal {O}}_{K}$ Against this background, Ernst Eduard Kummer developed the idea of "ideal numbers", which is, however, considered obsolete. It can be shown that every non-trivial integer ideal ${\mathfrak {a}}\subset {\mathcal {O}}_{K}$ has a unique multiplicative decomposition into prime ideals. This finally allows the definition of a zeta function

$\zeta _{K}(s)=\sum _{{\mathfrak {a}}\subset {\mathcal {O}}_{K}}{\frac {1}{N({\mathfrak {a}})^{s}}},$

which decays into an Euler product over the prime ideals:

$\zeta _{K}(s)=\prod _{\mathfrak {p}}{\frac {1}{1-N({\mathfrak {p}})^{-s}}}.$

Here the natural number denotes $N({\mathfrak {a}})$ the norm of the ideal ${\mathfrak {a}}$ (a measure of its "density" in ${\mathcal {O}}_{K}$ ).

The function $\zeta _{K}(s)$ has a holomorphic continuation to $\mathbb {C} \setminus \{1\}$ , has a first order pole in s=1 and satisfies a functional equation. It has great number theoretic relevance, since on the one hand it extends the concept of Riemann's conjecture to number fields, on the other hand it encodes in the class number formula "how much" the prime factorization in ${\mathcal {O}}_{K}$ deviates from uniqueness. This measure is also known as the class number.

The number body ${\mathbb {Q}}$

In the case $K=\mathbb {Q}$ the Dedekind zeta function $\zeta _{\mathbb {Q} }(s)$ just the Riemann zeta function. In particular, this is related to the prime elements in their integral ring $\mathbb {Z}$ .

Square Number Bodies

Is $K/\mathbb {Q}$ a quadratic extension of ${\mathbb {Q}}$ with discriminant , then there is a Dirichlet character χ $\chi _{D}$ modulo $|D|$ so that

$\zeta _{K}(s)=\zeta (s)L(\chi _{D},s),$

where denotes $L(\chi _{D},s)$ the Dirichlet L-function associated with χ $\chi _{D}$

An important special case is $K=\mathbb {Q} ({\sqrt {-1}})$ . The corresponding zeta function is given by

$\zeta _{\mathbb {Q} ({\sqrt {-1}})}(s)=\zeta (s)\beta (s),$

where the Dirichlet beta function β corresponds to $\beta (s)$ the character χ $\chi _{4}(1)=-\chi _{4}(-1)=1$ modulo 4. This gives directly the following identity for the Dirichlet series of the sum-of-squares function $r_{2}(n)$ :

$4\zeta (s)\beta (s)=\sum _{n=1}^{\infty }{\frac {r_{2}(n)}{n^{s}}}.$

Via a coefficient comparison, one can thus $r_{2}(n)$ conclude a closed formula for the Among other things, this provides an analytical proof that a prime number is exactly the sum of two squares, i.e. $p=n^{2}+m^{2}$ if $p\not \equiv 3\mod 4.$

Circular divider

If $K=\mathbb {Q} (\mu _{m})$ the body of -th unit roots, also called circle-dividing body, then the following applies

$\zeta _{K}(s)=\zeta (s)\prod _{\chi \not =\chi _{0}}L(\chi ,s).$

The product passes through all primitive characters modulo so that $l|m$ with the exception of the trivial character χ $\chi _{0}$ which only takes the value 1. Since both $\zeta (s)$ and s=1 have $\zeta _{K}(s)$ simple poles at , it follows that $L(\chi ,1)\not =0$ holds for all characters. A consequence of this statement is Dirichlet's prime number theorem.

Abelian extensions

In the case that $K/\mathbb {Q}$ is an Abelian extension, the quotient $\zeta _{K}(s)/\zeta (s)$ an integer function. In a sense, this means that the Riemann zeta function in this case is a "divisor of $\zeta _{K}(s)$ " (Aramata-Brauer theorem). That this is also true for non-Abelian extensions is the subject of deep number-theoretic conjectures, for example the Dedekind conjecture or the Artin conjecture.

Quaternions and octaves

Using the Cayley-Dickson method, one can determine Dirichlet series from the quaternions and octaves, which $r_{8}(n)$ contain the sum-of-squares function $r_{4}(n)$ or namely

$8(1-2^{2-2s})\ \zeta (s)\ \zeta (s-1)=\sum _{n=1}^{\infty }{\frac {r_{4}(n)}{n^{s}}},$

and also

$16(1-2^{1-s}+2^{4-2s})\ \zeta (s)\ \zeta (s-3)=\sum _{n=1}^{\infty }{\frac {r_{8}(n)}{n^{s}}}.$

From this follows directly, among other things, the four-square theorem and Jacobi's theorem.

Richard Dedekind

Connections to the theory of automorphic forms

In the theory of modular forms, which are important for number theory, the Riemann zeta function appears in a few places.

-functions to ironstone series

For weights $k=2,4,6,\dots$ the normalised Eisenstein series to the full moduli group $\mathrm {SL} _{2}(\mathbb {Z} )$ defined as follows:

$E_{k}(z):={\frac {1}{2\zeta (k)}}\sum _{(n,m)\in \mathbb {Z} ^{2}\setminus \{(0,0)\}}{\frac {1}{(nz+m)^{k}}}=1-{\frac {2k}{B_{2k}}}\sum _{n=1}^{\infty }\sigma _{k-1}(n)\mathrm {e} ^{2\pi \mathrm {i} z}.$

The latter expression is a representation as a Fourier series. This is characteristic for modular forms. Due to the normalisation by means of the factor $1/2\zeta (2k)$ this now has exclusively rational coefficients. This is used in number theory, among other things, to prove integer identities between divisor functions. Because of their relation to divisor functions (the coefficients of the Fourier series belonging to $E_{k}$ ), $-2k/B_{2k}\cdot \zeta (s)\zeta (s-k+1)$ are the L-functions belonging to $E_{k}$ This principle generalises to congruence subgroups for Eisenstein series. Here the constant coefficients are related to values of L-functions to Dirichlet characters.

In 1987 Frits Beukers was able to prove the irrationality of $\zeta (3)$ with the help of the theory of Eisenstein series. For this he considered the function

$F(z)={\frac {1}{40}}\left(E_{4}(z)-36E_{4}(6z)-28E_{4}(2z)+63E_{4}(3z)\right),$

which $\Gamma _{1}(6)$ is a modular form to weight 4 for the congruence subgroup Γ The L-function corresponding to this is then

$L(F,s)=6\left(1-{\frac {36}{6^{s}}}-{\frac {28}{2^{s}}}+{\frac {63}{3^{s}}}\right)\zeta (s)\zeta (s-3).$

The argument ultimately refers to a technique that exploits radii of convergence of inverse functions of locally injective meromorphic functions. The same method can be used to find $\zeta (2)=\pi ^{2}/6\notin \mathbb {Q}$ and $8\zeta (3)-5{\sqrt {5}}L(\chi _{5};3)\notin \mathbb {Q} ({\sqrt {5}})$ , where the character χ is $\chi _{5}$ the Legendre symbol modulo 5. However, according to Beukers himself, the techniques most probably cannot be applied to the cases $\zeta (5),\zeta (7),\dotsc$ but give insight into algebraic geometric and modular interpretations of the Apery numbers.

Relationship to non-holomorphic ironstone series

For complex numbers $z=x+y\mathrm {i}$ with y > 0 {\displaystyle the Eisenstein series $\operatorname {Re} (s)>1$

$E(z,s)={\frac {1}{2}}\pi ^{-s}\Gamma (s)\sum _{(n,m)\in \mathbb {Z} ^{2}\setminus \{(0,0)\}}{\frac {y^{s}}{|nz+m|^{2s}}}$

absolute. The function defined by this is non-holomorphic and also (for fixed ) invariant in under the effect of the full moduli group. Moreover, it can be continued (for fixed ) in meromorphically into the whole plane with simple poles in $s=0$ and s=1 , the functional equation holds

$E(z,1-s)=E(z,s).$

This parallel to the theory of the zeta function already suggests a connection. The representation applies

$E(z,s)={\frac {1}{2}}\pi ^{-s}\Gamma (s)\zeta (2s)\sum _{M\in \Gamma _{\infty }\backslash \mathrm {SL} _{2}(\mathbb {Z} )}\operatorname {Im} ((M(z))^{s}),$

where Γ $\Gamma _{\infty }$ the subgroup of translations of _{2} $\mathrm {SL} _{2}(\mathbb {Z} )$ . If one also considers the Fourier expansion

$E(z,s)=\sum _{r=-\infty }^{\infty }a_{r}(y,s)\mathrm {e} ^{2\pi \mathrm {i} xr},$

so applies

$a_{0}(y,s)=\pi ^{-s}\Gamma (s)\zeta (2s)y^{s}+\pi ^{s-1}\Gamma (1-s)\zeta (2-2s)y^{1-s}.$

Non-holomorphic Eisenstein series, and thus the zeta function itself, play a fundamental role in the so-called Rankin-Selberg method, which has emerged as a powerful tool in investigations within the Langlands programme.

Relationship to the Jacobian theta function

A very important property of the Riemann zeta function is its functional equation. This is expressed most simply via

$\Gamma \left({\frac {s}{2}}\right)\ \pi ^{-s/2}\ \zeta (s)=\Gamma \left({\frac {1-s}{2}}\right)\ \pi ^{(s-1)/2}\ \zeta (1-s)$

and note that on the right hand side, amazingly, the complex variable is simply replaced by 1-s

There are several derivation variants for finding this equation. Riemann already showed two different ones. One of them includes a simple special case of the Jacobian theta function

$\theta (x):=\vartheta (0,ix)=\sum _{n=-\infty }^{\infty }\mathrm {e} ^{-\pi xn^{2}}$

directly with it. Of advantage is the modification ψ $\textstyle \psi (x)=\sum _{n=1}^{\infty }\mathrm {e} ^{-\pi xn^{2}}$ , it holds that ψ $\psi (x)=(\theta (x)-1)/2$ . The theta function is thereby a modular form of half-whole weight: with Poisson's summation formula Jacobi already found the identity θ $\theta (x)=\theta \left(1/x\right)/{\sqrt {x}}$ from which immediately $\psi \left(1/x\right)={\sqrt {x}}\psi (x)+{\sqrt {x}}/2-1/2$ follows ψ

The starting point is the integral representation

$\Gamma \left({\frac {s}{2}}\right)\ \pi ^{-s/2}\ \zeta (s)=\int \limits _{0}^{\infty }\sum _{n=1}^{\infty }\mathrm {e} ^{-\pi tn^{2}}t^{s/2}{\frac {\mathrm {d} t}{t}}=\int \limits _{0}^{\infty }\psi (t)t^{s/2}{\frac {\mathrm {d} t}{t}}.$

The following trick is a standard transformation in the proof of Heck's inverse theorem. By splitting the integral into the intervals $[1,\infty [$ and [0,1] where in the latter the substitution $t={\tfrac {1}{x}}$ follows:

${\begin{aligned}\int \limits _{0}^{\infty }\psi (t)t^{s/2}{\frac {\mathrm {d} t}{t}}&=\int \limits _{1}^{\infty }\psi (t)t^{s/2}{\frac {\mathrm {d} t}{t}}-\int \limits _{\infty }^{1}\psi \left({\frac {1}{x}}\right)x^{-s/2}{\frac {\mathrm {d} x}{x}}\\&=\int \limits _{1}^{\infty }\psi (x)x^{s/2}{\frac {\mathrm {d} x}{x}}+\int \limits _{1}^{\infty }\left({\sqrt {x}}\psi (x)+{\frac {\sqrt {x}}{2}}-{\frac {1}{2}}\right)x^{-s/2}{\frac {\mathrm {d} x}{x}}\\&=\int \limits _{1}^{\infty }\psi (x)\left[x^{s/2}+x^{(1-s)/2}\right]{\frac {\mathrm {d} x}{x}}+{\frac {1}{2}}\int \limits _{1}^{\infty }\left[x^{(1-s)/2}-x^{-s/2}\right]{\frac {\mathrm {d} x}{x}}.\end{aligned}}$

The second integral can be calculated elementarily:

$\Gamma \left({\frac {s}{2}}\right)\ \pi ^{-s/2}\ \zeta (s)=\int \limits _{1}^{\infty }\psi (x)\left[x^{s/2}+x^{(1-s)/2}\right]{\frac {\mathrm {d} x}{x}}-{\frac {1}{s(1-s)}}.$

As one can easily see, the right side is unchanged under the mapping $s\mapsto 1-s$ , from which the functional equation already follows. This reasoning is justified because the integral on the right-hand side now exists for all $s\in {\mathbb {C}}$ exists.

Carl Gustav Jacobi

Geometric aspects

Volumes of special geometric figures

The values of the Riemann zeta function at positive even places are rational multiples of corresponding π $\pi$ powers. These values have a geometric interpretation in some ways.

For example, they appear in the formula for the symplectic volume of the fundamental domain $F_{n}$ Siegel's moduli group on Siegel's upper Hable plane $H_{n}$ Strictly speaking, Siegel showed the formula

$\operatorname {Vol} (F_{n})=2\pi ^{-{\frac {n(n+1)}{2}}}\prod _{k=1}^{n}(k-1)!\zeta (2k).$

In the simplest case n=1 this formula reduces to the hyperbolic volume of the fundamental domain of the full moduli group. This case was generalised by Don Zagier to more general hyperbolic manifolds. Here the volumes are related to values $\zeta _{K}(2)$ the Dedekind zeta function. Corresponding higher-dimensional generalisations also lead to far-reaching conjectures in the environment of K-theory and the Bloch groups. A review paper on this from the year 2000 was written by Herbert Gangl and Don Zagier.

Beilinson's assumption

$n=2,3,4,\dots$ Beilinson, Bloch and Kato have found further insight into the values $\zeta (2n-1)$ for higher K-groups $K_{i}(\mathbb {Z} )$ of the algebraic K-theory play an important role. For these there exists an isomorphism

$r\colon K_{4n-1}(\mathbb {Z} )\otimes _{\mathbb {Z} }\mathbb {R} \longrightarrow \mathbb {R} .$

Here is $\otimes$ the tensor product of two $\mathbb{Z }$ moduli. The image $R_{2n}$ of a non-zero element in $K_{4n-1}(\mathbb {Z} )\otimes _{\mathbb {Z} }\mathbb {Q}$ is called the -th regulator. It is uniquely determined except for one rational factor and the following applies

$\zeta (2n-1)\equiv R_{2n}\mod \mathbb {Q} ^{\times }.$

This discovery by Armand Borel had a great impact on further research and gave deep insights into the arithmetic nature of zeta and L values. These were eventually unified in the so-called Beilinson conjecture. Spencer Bloch and Kazuya Kato gave a complete description of the values $\zeta (2n-1)$ (i.e. not only mod $\mathbb {Q} ^{\times }$ ) by a new theory of so-called Tamagawa measures.

Relationships to elliptic curves and congruent triangles

→ Main article: Elliptic curve

The (global) Hasse-Weil -function of an elliptic curve over $\mathbb {Q}$ has the shape

$L(E_{n};s)={\frac {\zeta (s)\zeta (s-1)}{\prod _{p\,\mathrm {Primzahl} }Z(E_{n}/\mathbb {F} _{p};p^{-s})}},$

where $E_{n}$ denote $Z(E_{n}/\mathbb {F} _{p};T)$ the local zeta functions to

→ Main article: Congruent number

A triangle is called congruent if it is right-angled, has only rational side lengths and an integer area The number is accordingly called a congruent number. A number is a congruent number exactly if the associated elliptic curve $E_{n}:y^{2}=x^{3}-nx$ has infinitely many rational points. If the weak conjecture of Birch and Swinnerton-Dyer holds, this is the case exactly if $L(E_{n};1)=0$ . Under this condition, the Hasse-Weil function defined above encodes the geometric properties of the numbers with respect to congruence.

Arithmetic zeta functions

The zeta function of a scheme (of finite type over the integers) is defined by the Euler product

$\zeta _{X}(s):=\prod _{x\in X}{\frac {1}{1-N(x)^{-s}}}.$

The product passes through all closed points of the schema, i.e. those whose associated residue class body is finite. $N(x)$ denotes the number of elements of this body. The affine scheme $X=\operatorname {Spec} (\mathbb {Z} )$ is then associated with the Riemann zeta function.

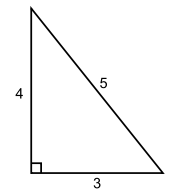
The right-angled triangle has rational side lengths of 3, 4 and 5, but an integer area of 6. Therefore 6 is a congruent number.

Each region outlined in blue is a fundamental area of the full module group on the upper half level. The standard region is highlighted in grey. The hyperbolic volume of each such figure corresponds exactly to π $\pi /3$ .

Occurrence in probability theory, statistics and probabilistic number theory.

Partial alien tuples

Some probability laws from number theory are also closely related to the zeta function. The probability that a randomly chosen number is square-free, and likewise the probability that two randomly chosen numbers are divisor-alien, is equal to

${\frac {1}{\zeta (2)}}={\frac {6}{\pi ^{2}}}=0{,}60792\ 71018\ 54026\ 62866\ldots$ (sequence A059956 in OEIS).

More generally, is $1/\zeta (nk)$ the probability that positive integers do not have a -th power greater than 1 as a common divisor.

Relationships to the theory of random matrices

In 1972, during a tea break at the Princeton Institute for Advanced Studies, mathematician Hugh Montgomery described his model for the pair correlation of zeros of the zeta function to a colleague, quantum physicist Freeman Dyson. Assuming the Riemann conjecture, the non-trivial zeros ρ $\rho _{n}=1/2\pm \mathrm {i} t_{n}$ with real In the following the normalisation

$w_{n}={\frac {t_{n}}{2\pi }}\log \left({\frac {t_{n}}{2\pi }}\right)$

considered. Together with $N(W):=\#\{n\in \mathbb {N} |w_{n}<W\}$ we get lim $\textstyle \lim _{W\to \infty }{\frac {N(W)}{W}}=1.$ As a further procedure, for numbers α $\alpha <\beta$ the pair correlation $\textstyle {\frac {1}{W}}\#\{(w_{n},w_{m})\in [0,W]^{2}|\alpha \leq w_{n}-w_{m}\leq \beta \}$ and more generally the linear operator for functions $f\colon \mathbb {R} \to \mathbb {R}$

$R_{2}(f,W):={\frac {1}{W}}\sum _{1\leq j,k\leq N(W) \atop j\not =k}f(w_{j}-w_{k})$

can be studied. The following theorem of Montgomery, proved under the assumption of the Riemann conjecture, classifies the asymptotic behaviour of $R_{2}$ for a wide class of functions : If the Fourier transform of compact carrier with $K\subset [-1,1]$ , it follows

$\lim _{W\to \infty }R_{2}(f,W)=\int \limits _{-\infty }^{\infty }f(x)\left(1-\left({\frac {\sin(\pi x)}{\pi x}}\right)^{2}\right)\mathrm {d} x.$

Dyson, one of the founders of the theory of random matrices, immediately recognised a connection. Namely, if $(e^{\mathrm {i} \theta _{1}},\dotsc ,e^{\mathrm {i} \theta _{N}})$ with $0\leq \theta _{j}<2\pi$ are the eigenvalues of an element the unitary group $U(N)$ and will ϕ $\textstyle \phi _{n}:={\frac {N}{2\pi }}\theta _{n}$ , then the following follows as above

$\lim _{N\to \infty }\int _{U(N)}\sum _{j\not =k}f(\phi _{j}-\phi _{k})\mathrm {d} \mu _{U(N)}(A)=\int \limits _{-\infty }^{\infty }f(x)\left(1-\left({\frac {\sin(\pi x)}{\pi x}}\right)^{2}\right)\mathrm {d} x.$

Here μ denotes $\mu _{U(N)}$ the Haar measure on $U(N)$ . The similarity of both formulae indicates a strong connection of the theory of the zeta function to the theory of unitary random matrices. This connection is underlined by the so-called Polya-Hilbert program: if the values γ $\gamma _{n}$ all non-trivial zeros $1/2+i\gamma _{n}$ written as eigenvalues of a (self-adjoint) Hamilton operator, the Riemann conjecture follows.

Keating-Snaith conjecture

Keating and Snaith have formulated a conjecture about the asymptotic growth of the power moments $\textstyle I_{k}(T)=\int _{0}^{T}|\zeta (1/2+\mathrm {i} t)|^{2k}\mathrm {d} t$ the zeta function. This states that for all

$I_{k}(T)\sim M(k)A(k)T(\log(T))^{k^{2}},$

with the arithmetic factor

$A(k):=\prod _{p\ \mathrm {Primzahl} }\left(1-{\frac {1}{p}}\right)^{k^{2}}\left(\sum _{m=0}^{\infty }\left({\frac {(k+m-1)!}{m!(k-1)!}}\right)^{2}{\frac {1}{p^{m}}}\right),$

and the matrix factor

$M(k):=\prod _{j=0}^{k-1}{\frac {j!}{(j+k)!}}.$

To understand the way to this assumption and its relation to statistics, the following very heuristic argument is helpful. Assuming that all primes are "independently distributed", it follows by means of Euler product for the expected value (with respect to the Lebesgue measure $\mathrm {d} t/T$ on $[1/2,1/2+\mathrm {i} t]$ )

${\frac {I_{k}(T)}{T}}=\operatorname {E} [|\zeta (s)|^{2k}]=\prod _{p\ \mathrm {Primzahl} }\operatorname {E} \left[\left|{\frac {1}{1-p^{-s}}}\right|^{2k}\right],$

and from this one ultimately obtains the terms given by Keating and Snaith, whereby the matrix factor is only a correction term within this "independence model".

Nina Snaith

Algorithms for fast numerical calculation

→ Main article: Calculation method for the Riemann zeta function

For a quick numerical calculation of the function $\zeta (s)$ many classical forms of representation are useless. In particular, these include the Dirichlet series, the Euler product, the representation as a Mellin transformation and the Hadamard product. For efficient performance, a finite approximate sum expression with high convergence speed is most suitable.

Euler-Maclaurin molecular formula

A good and historically early used method turns out to be the "aborted" summation formula, which is obtained with the help of the Euler-Maclaurin summation formula. In general, an arbitrary natural number first specified, for which should also N>|s| It then holds:

${\begin{aligned}\zeta (s)=&\sum _{n=1}^{N-1}{\frac {1}{n^{s}}}+{\frac {N^{1-s}}{s-1}}+{\frac {1}{2}}N^{-s}+\sum _{r=1}^{p-1}{\frac {B_{2r}}{(2r)!}}s(s+1)\cdots (s+2r-2)N^{-s-2r+1}+R_{2p}(s).\end{aligned}}$

The following applies to the remainder

$|R_{2p}(s)|\leq \left|{\frac {s(s+1)\cdots (s+2p-1)B_{2p}N^{-s-2p+1}}{(2p)!(\operatorname {Re} (s)+2p-1)}}\right|.$

With the (free) choice of should also be noted that the remainder element only converges on the half-plane $\operatorname {Re} (s+2p)>1$ . Therefore, $p>-\operatorname {Re} (s/2)$ hold. For increasing values of the error $R_{2p}$ therefore decreases rapidly.

Moreover, by applying the functional equation (a quick calculation of the gamma function and the exponential function π $\pi ^{s}$ is easy to implement), σ can be $\sigma >0$ assumed without restriction. Here the summation formula is clearly faster. A disadvantage of this method, however, is that it loses efficiency for growing imaginary parts.

Alternating sums

A method using broken alternating series was developed by Borwein. This uses the formula valid for $\operatorname {Re} (s)>-(N-1)$ formula

$\zeta (s)={\frac {1}{1-2^{1-s}}}\left(\sum _{k=1}^{N}{\frac {(-1)^{k-1}}{k^{s}}}+{\frac {1}{2^{N}}}\sum _{k=N+1}^{2N}{\frac {(-1)^{k-1}e_{k-N}}{k^{s}}}\right)+E_{N}(s),$

where $\textstyle e_{k}=\sum _{j=k}^{N}{N \choose j}$ also depends on the choice of error $E_{N}(s)$ falls at an exponential rate. However, it is also true here that the method loses efficiency for larger imaginary parts.

Calculation on the critical straight line

Riemann Seal Formula

Many methods lose precision if the imaginary part of the argument is chosen very large, which is problematic when searching for zeros along the critical straight line. Therefore, other methods are used here, one of which is the Riemann-Siegel formula. This can be derived via the Riemann-Siegel function:

$Z(t)=\mathrm {e} ^{\mathrm {i} \theta (t)}\zeta ({\tfrac {1}{2}}+\mathrm {i} t).$

Here θ $\theta (t)$ also called the Riemann-Siegel theta function. For values $m={\bigg \lfloor }{\sqrt {t/2\pi }}{\bigg \rfloor }$ follows with the Approximate functional equation

$Z(t)=\mathrm {e} ^{\mathrm {i} \theta (t)}\sum _{n=1}^{m}{\frac {1}{n^{{\frac {1}{2}}+\mathrm {i} t}}}+\mathrm {e} ^{-\mathrm {i} \theta (t)}\sum _{n=1}^{m}{\frac {1}{n^{{\frac {1}{2}}-\mathrm {i} t}}}+O(t^{-{\frac {1}{4}}})=2\sum _{n=1}^{m}{\frac {\cos(\theta (t)-t\log n)}{\sqrt {n}}}+O(t^{-{\frac {1}{4}}}).$

The error term $O(t^{-{\frac {1}{4}}})$ can be obtained by an asymptotic evolution

$(-1)^{m+1}\left({\frac {t}{2\pi }}\right)^{-{\frac {1}{4}}}\sum _{j=0}^{M}(-1)^{j}\left({\frac {t}{2\pi }}\right)^{-{\frac {j}{2}}}\Phi _{j}(2(t-m)-1)+R_{M}(t),\,\,\,\,R_{M}(t)=O(t^{-(2M+3)/4}),$

can be improved at will. The terms $\Phi$ are elementary computable, but become more complicated with increasing index. Altogether, a fairly precise calculation results in an effort of $O(t^{1/2})$ operations in the form of term calculations with subsequent addition. In order to find zeros, it is sufficient to identify areas with sign changes (and then perform interval nesting for their precise determination).

Proceedings of Odlyzko and Schönhage

→ Main article: Proceedings of Odlyzko and Schönhage

In 1988, A. M. Odlyzko and A. Schönhage developed a very fast method to determine values of the Riemann zeta function on the critical straight line. This is based on the ideas of the Riemann-Siegel formula, but only requires instead of $O(t^{\varepsilon })$ $O(t^{1/2})$ computational operations, where ε can be chosen $\varepsilon >0$ small. The refinement of the calculation techniques is based on the fast Fourier transform.

Other expressions for the zeta function

In addition to its elementary row representation, the zeta function has a rich array of other expressions, some of which are listed below.

Row representations

Worth mentioning is the series expression

$\zeta (s)={\frac {1}{s-1}}+1-\sum \limits _{n=1}^{\infty }(\zeta (s+n)-1){\frac {s(s+1)\cdots (s+n-1)}{(n+1)!}}$ ,

which is $s\neq 1,0,-1,\dotsc$ defined for all values is interesting about this is that the zeta function can thus be continued recursively to the whole number plane, since $\zeta (s)$ only the values $\zeta (s+1),\zeta (s+2),\dotsc$ needed for the calculation of

From Helmut Hasse comes the globally convergent series

$\zeta (s)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}\left({n \atop k}\right){\frac {(-1)^{k-1}}{(k+1)^{s-1}}}.$

Blagouchine gave numerous variations and generalisations of such series types in 2018.

Integral representations

An exotic and globally convergent expression is obtained by directly inserting the elementary row representation of the zeta function into the Abel-Plana summation formula:

$\zeta (s)={\frac {1}{s-1}}+{\frac {1}{2}}+2\int \limits _{0}^{\infty }{\frac {\sin(s\arctan t)}{(1+t^{2})^{\frac {s}{2}}\ (\mathrm {e} ^{2\,\pi \,t}-1)}}\,\mathrm {d} t$

Quite similarly, for example

$\zeta (s)=2^{s-2}\int \limits _{-\infty }^{\infty }{\frac {\tan \left({\frac {\pi }{2}}\,\mathrm {i} \,t\right)}{{(1+\mathrm {i} \,t)}^{s}}}\,\mathrm {d} t$ ,

whereby, however, the integral converges restrictively only for $\operatorname {Re} (s)>1$ .

An overview of numerous other integral representations comes from Michael S. Milgram.

Sum formulae

To derive a globally valid summation formula, in the case of the Mellin transform, the integrand is an t=0 analytic function around addition to the kernel function t $t^{s-2}$

${\frac {t}{\mathrm {e} ^{t}-1}}=\sum _{\nu =0}^{\infty }{\frac {B_{\nu }}{\nu !}}t^{\nu }.$

This fact creates a close relationship between the zeta function and the Bernoulli numbers $B_{\nu }$ . By successively splitting off the Taylor polynomials from $t/(\mathrm {e} ^{t}-1)$ in the integration interval from 0 to 1 the zeta function can be applied to the whole of $\mathbb {C} \setminus \{1,0,-1,\dotsc \}$ be continued:

$\zeta (s)={\frac {1}{\Gamma (s)}}\left({\frac {1}{s-1}}-{\frac {1}{2s}}+\sum \limits _{\nu =2}^{\infty }{\frac {B_{\nu }}{\nu !}}{\frac {1}{s+\nu -1}}+\int \limits _{1}^{\infty }{\frac {x^{s-1}}{\mathrm {e} ^{x}-1}}\,\mathrm {d} x\right).$

This exploits the fact that $1/\Gamma (s)$ is an integer function.

Relationships to other special functions and further generalisations

In the desire to generalise or vary the definition of the Riemann zeta function, numerous related functions were introduced and investigated. Often these also bear the name "zeta function", connected with the name of their "discoverer". Against this background, reference should also be made to the list of Zeta functions.

Connection to other Zeta functions and Dirichlet series

It applies

$\zeta (s)={\frac {\eta (s)}{1-2^{1-s}}}={\frac {\lambda (s)}{1-2^{-s}}}$

where η $\eta (s)$ and λ $\lambda (s)$ denote the Dirichlet eta and lambda function, respectively.

→ Main article: Hurwitz zeta function

The Hurwitz zeta function is defined for $\operatorname {Re} (s)>1$ Re by $\operatorname {Re} (q)>0$

$\zeta (s,q)=\sum _{n=0}^{\infty }{\frac {1}{(n+q)^{s}}}.$

For fixed it has an analytic continuation on $\mathbb {C} \setminus \{1\}$ with a simple pole in . For $q=1$ now holds:

$\zeta (s)=\zeta (s,1).$

With the help of the Hurwitz zeta function, the Riemann zeta function and the Dirichlet L-functions can be treated uniformly. This is particularly useful with regard to their generalised functional equation.

→ Main article: Lerch's zeta function

Even more general than the Hurwitz zeta function is the Lerch zeta function, which for $\operatorname {Re} (s)>1$ , $\operatorname {Re} (q)>0$ Im $\operatorname {Im} (\lambda )\geq 0$ is given by

$L(\lambda ,q,s)=\sum _{n=0}^{\infty }{\frac {\mathrm {e} ^{2\pi \mathrm {i} \lambda }}{(n+q)^{s}}}.$

It then applies

$\zeta (s)=L(0,1,s).$

The far-reaching definition of Lerch's zeta function not only allows specialisations to the Hurwitz and thus also to the Riemann zeta function, but also includes many other important functions as special cases. Similarly defined "generalised zeta functions" are also used in theoretical physics, namely in connection with the systematic so-called semiclassical approximation of quantum mechanical results.

→ Main article: Primzeta function

For all with holds $\operatorname {Re} (s)>1$

$\log \zeta (s)=\sum _{{n=1}}^{\infty }{\frac {P(ns)}{n}},$

where P(s) with $\textstyle P(s):=\sum _{p\ {\text{Primzahl}}}{\frac {1}{p^{s}}}$ denotes the prime function. Möbius inversion can be used to derive a way to quickly obtain the prime function from a series over logarithmised zeta functions:

$P(s)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\log \zeta (ns).$

This allows an (analytical) continuation of the prime function into elementary areas of the half-plane $\{s\in \mathbb {C} \mid \operatorname {Re} (s)>1\}\subset E\subset \{s\in \mathbb {C} \mid \operatorname {Re} (s)>0\}$ where all functions $\log \zeta (sn)$ with $n=1,2,3,\dotsc$ are holomorphic. Moreover, the formula can be used for a quick numerical calculation of the primezeta function. For example, Henri Cohen found within a few milliseconds:

$\sum _{p\ {\text{Primzahl}}}{\frac {1}{p^{2}}}=0{,}45224742004106549850654336483224793417323134323989\dots$

Furthermore, it follows from $P(s)\sim \log \zeta (s)$ for $s\to 1$ , that the series $1/2+1/3+1/5+\dotsb$ of reciprocal primes diverges.

Relationship to the polylogarithm

→ Main article: Polylogarithm

The polylogarithm generalises, among others, the natural logarithm and is given for $|z|<1$ by the power series

$\operatorname {Li} _{s}(z)=\sum _{n=1}^{\infty }{\frac {z^{n}}{n^{s}}}.$

Furthermore, if $\operatorname {Re} (s)>0$ then this series is also convergent at the boundary values $|z|=1$ (except for $z=1$ ) convergent. In general, for fixed an analytic continuation in on the set $\mathbb {C} \setminus \mathbb {R} _{\geq 1}$ possible. It is true for all $\operatorname {Re} (s)>1$

$\zeta (s)=\operatorname {Li} _{s}(1),$

but also

$\zeta (s)={\frac {\operatorname {Li} _{s}(-1)}{2^{1-s}-1}}$

for values $s\in \mathbb {C}$ with $s\not =1$ . In particular, for all $s\in \mathbb {C}$ the limit value:

$(2^{1-s}-1)\zeta (s)=\lim _{z\to -1^{+}}\sum _{n=1}^{\infty }{\frac {z^{n}}{n^{s}}}.$

Relationship to the polygamy function

→ Main article: Polygamma function

The function $f(z)=\log \Gamma (1+z)$ is holomorphic on the entire half-plane $\operatorname {Re} (z)>-1$ since the logarithmic part Γ has no zeros or poles there. Consequently, $\Gamma (1+z)$ around the point z = 0 can be developed into a Taylor series. The coefficients of this series are directly related to the values of the zeta function at positive integers: For all with $|z|<1$ formula applies

$\log \Gamma (1+z)=-\gamma z+\sum _{n=2}^{\infty }(-1)^{n}{\frac {\zeta (n)}{n}}z^{n}.$

For the digamma function

$\psi (1+z)=-\gamma -\sum _{n=1}^{\infty }(-1)^{n}\zeta (n+1)z^{n},$

and generally for natural numbers $m>0$

$\psi _{m}(1+z)=\sum _{k=0}^{\infty }(-1)^{m+k+1}(m+k)!\;\zeta (m+k+1)\;{\frac {z^{k}}{k!}}.$

At first sight, this creates a connection to the theory of polygamma functions, which arise from the derivatives of the function $\log \Gamma (z)$ by definition. The th derivative of just corresponds to the $\log \Gamma (z)$ th polygamma function ψ $\psi _{n}(z)$ . Correspondingly non-trivial is the question how a general polygamma function ψ could $\psi _{s}(z)$ be developed which can also evaluate arbitrary complex-valued arguments and still carries a structure as analytic as possible. The reason for this is that the obvious approach of explaining an -th derivation is not easy to implement. However, it turns out that the above Taylor series, when the good properties of the zeta function are invoked, provides a good generalisation relatively directly. Espinosa and Moll $\psi _{s}(z)$ introduced such a generalised polygamma function ψ 2003, which is now even defined for all complex values This has for $s\neq 0,1,2,\dotsc$ the general Taylor development

$\psi _{s}(1+z)=\sum _{n=0}^{\infty }{\frac {1}{\Gamma (-s-n)}}\left(\zeta '(s+n+1)+\left(\sum _{k=1}^{\infty }{\frac {1}{k}}-{\frac {1}{k-s-n-1}}\right)\zeta (s+n+1)\right){\frac {z^{n}}{n!}},$

valid in the range However, this generalisation does not use fractional infinitesimal calculus. Such an approach was taken by Grossman.

Values of the Riemann zeta function also appear as function values of the polygamma function. Worth mentioning in this context is a set of formulae which for any natural $n>1$ are given by

$\zeta (s)={\frac {\Gamma (1-s)}{n^{s}\log n}}\left(\sum \limits _{k=1}^{n-1}\psi _{s-1}\left({\frac {k}{n}}\right)-\left(n^{s}-1\right)\psi _{s-1}(1)\right).$

Diagram of the function $\operatorname {Li} _{-2}(z)$ . Clearly seen: If the expression $z+4z^{2}+9z^{3}+16z^{4}+\cdots$ -1 from the right, this yields the value 0 - this corresponds to $\zeta (-2)$ .

Derivative

In recent decades, there has also been increasing $\zeta '(s)$ research on the properties of the derivative

The function $\zeta '(s)$ has a holomorphic continuation on all of $\mathbb {C} \setminus \{1\}$ with a second order pole in . It also satisfies a functional equation which is obtained by deriving the ordinary functional equation of the zeta function on both sides.

Although the derivative does not have a representation as an Euler product, there are also connections to the primes here. Such a formula can be obtained by means of logarithmic derivation, i.e. via the identity

${\frac {\left(\prod _{k}f_{k}\right)'}{\prod _{k}f_{k}}}=\sum _{k}{\frac {f'_{k}}{f_{k}}}.$

Set here

$f_{k}={\frac {1}{1-{\frac {1}{p_{k}^{s}}}}}$

for the -th prime number, the result is

$\zeta '(s)=-\zeta (s)\sum _{p\ {\text{Primzahl}}}{\frac {\log p}{p^{s}-1}}.$

The zeros are also of number-theoretical interest for the derivation. Thus the statement $\zeta '(s)\not =0$ in the strip $\{s\in \mathbb {C} \mid 0<\operatorname {Re} (s)<1/2\}$ the Riemann conjecture. The real zeros in the negative domain are given asymptotically by

$s_{n}=-2n+1+2^{2-2n}{\frac {\log(2)}{\pi ^{2}}}+{\frac {1}{n\pi ^{2}}}\left(1-{\frac {4q}{\pi }}\right)\left(1-{\frac {4p^{2}}{\pi ^{2}}}\right)\left(1+{\frac {2}{n\pi ^{2}}}\right)+O\left({\frac {1}{n^{3}}}\right),\quad n=2,3,4,\dots$

Where $p=\log(n/\pi )$ and $q=\arctan(2p/\pi )$ .

For all negative integers $-2n\in \{-2,-4,-6,-8,\dotsc \}$ one obtains via the functional equation

$\zeta '(-2n)=(-1)^{n}{\frac {\zeta (2n+1)(2n)!}{2^{{2n+1}}\ \pi ^{{2n}}}}.$

$\zeta '(-2n+1)={\frac {1}{2n}}\left[(-1)^{n+1}{\frac {2(2n)!}{(2\pi )^{2n}}}\zeta '(2n)+\left(\sum _{j=1}^{2n-1}{\frac {1}{j}}-\log(2\pi )-\gamma \right)B_{2n}\right].$

Other values are

$\zeta '(0)=-{\frac {1}{2}}\log 2\pi ,\quad \zeta '(-1)={\frac {1}{12}}-\log A,$

where denotes here the Glaisher-Kinkelin constant.

In Art and Culture

In the film The Poetry of Infinity, the Euler product development of the Riemann zeta function is written on a board in the background of Godfrey Harold Hardy's office.

In Neal Stephenson's novel Cryptonomicon, the Riemann zeta function is mentioned several times in connection with the fictional cryptocodes Azure, Pufferfish and Arethusa.