Finitary relation

A relation (Latin relatio "relation", "relationship") is generally a relationship that can exist between things. Relations in the sense of mathematics are exclusively those relationships for which it is always clear whether they exist or not; objects cannot therefore be in a relation to each other "to a certain degree". Thus, a simple set-theoretical definition of the term is possible: A relation is a set of -tuples. Things standing in relation each other form -tuples, which are elements of

Unless explicitly stated otherwise, a relation is commonly understood to be a two-digit or binary relation. In such a relation, two elements and form an ordered pair and (a,b). originate from different basic sets and the relation is called heterogeneous or "relation between the sets and ." If the basic sets match ( A = B ), then the relation is called homogeneous or "relation in or on the set ."

Important special cases, for example equivalence relations and order relations, are relations on a set.

Today, some authors do not necessarily consider the term relation to be restricted to sets, but allow any class consisting of ordered pairs to be considered a relation.

Definitions

Two-digit relation

A two-digit relation (also called binary relation) between two sets and is a subset of the Cartesian product $A\times B=\{(a,b)\mid a\in A,b\in B\}\colon$

$R\subseteq A\times B$ .

The set is called the source set (English: set of departure) of the relation set called the destination set (English: set of destination).

Sometimes, however, this definition is not precise enough and one includes the source and target set in the definition, the above subset is then called the graph $G_{R}$ the relation. A two-digit relation is then defined as a triple

$R=(G_{R},A,B)$ with $G_{R}\equiv \operatorname {Graph} (R)\subseteq A\times B$ .

The knowledge of source and target set is particularly important when functions are considered as special (so-called functional) relations.

The primal, argument or definition or pre-region of a given two-digit relation is understood to be the smallest possible pre-region to the graph $G_{R}$ whose elements all actually occur on the left-hand side in the ordered pairs of in characters

$Db(R)\equiv {\mathfrak {D}}(R):=\{a\mid \exists b\colon (a,b)\in G_{R}\}\subseteq A$ .

In this sense, the value set, value or image or after-range denotes the smallest after-range to $G_{R}$ given whose elements thus all occur in the pairs of on the right-hand side, in characters

$Wb(R)\equiv {\mathfrak {B}}(R):=\{b\mid \exists a\colon (a,b)\in G_{R}\}\subseteq B$ .

Occasionally, the term field (or node set) is used for the union set, in characters

$Fd(R)\equiv {\mathfrak {F}}(R):=Db(R)\cup Wb(R)=\{x\mid \exists x'\colon (x,x')\in G_{R}\lor (x',x)\in R\}\subseteq A\cup B$ .

In addition, the following designations can be found:

Domain $\operatorname {dom} R$ either for the (in principle arbitrarily large) source set or for the original image set (defined by the graph),
Co-domain (English codomain, range) $\operatorname {cod} R,\operatorname {ran} R$ either for the target set or for the image set,
Node set ( $\operatorname {ver} R$ ) for the field of a relation.

If two relations match in their graphs, they are also said to be essentially the same.
Example: Any relation $R=(G_{R},A,B)$ is essentially the same as $(G_{R},Db(R),Wb(R))$ and with the homogeneous relation $(G_{R},Fd(R),Fd(R))$ .

n-digit relation

More generally, an -digit relation a subset of the Cartesian product of sets $A_1, \dotsc, A_n$

$R\subseteq A_{1}\times \dotsb \times A_{n}$ with $A_{1}\times \dotsb \times A_{n}=\{(a_{1},\dotsc ,a_{n})\mid a_{1}\in A_{1},\dotsc ,a_{n}\in A_{n}\}=\textstyle \prod A$ .

Here $A=(A_{i})_{i\in \{1,\dots n\}}$ denotes the finite sequence of sets, and $\textstyle \prod A=\textstyle \prod _{i=1}^{n}A_{i}$ denotes the Cartesian product.

The more detailed definition can also be generalised to -digit relations and one then obtains the (n+1) -tuple

$R=(G_{R},A_{1},\dotsc ,A_{n})=(G_{R},A)$ with $G_{R}\equiv \operatorname {Graph} (R)\subseteq A_{1}\times \dotsb \times A_{n}=\textstyle \prod A$ .

The sets $A_{1},\dotsc ,A_{i},\dotsc ,A_{n}$ called carrier sets of the relation with the minimal carrier sets to the graph $G_{R}$ , namely

$Tr_{i}(R)\equiv {\mathfrak {T}}_{i}(R):=\{a_{i}\mid \exists a_{1},\dotsc ,a_{i-1},a_{i+1},\dotsc ,a_{n}\colon (a_{1},\dotsc ,a_{i-1},a_{i},a_{i+1},\dotsc ,a_{n})\in G_{R}\}$ .

The field of an -digit relation is given by

$Fd(R)\equiv {\mathfrak {F}}(R):=\textstyle \bigcup \{Tr_{i}(R)\mid 1\leq i\leq n\}\subseteq \textstyle \bigcup A$ .

Substantial equality is defined analogously as for two-digit relations by correspondence of the graphs, in particular every } -digit relation $R=(G_{R},A_{1},\dotsc ,A_{n})$ substantially equal to $(G_{R},Tr_{1}(R),\dotsc ,Tr_{n}(R))$ and with the homogeneous relation $(G_{R},\underbrace {Fd(R),\dotsc ,Fd(R)} _{n{\text{-mal}}})$ .

One-digit and zero-digit relation

A one-digit relation on a set is thus simply a subset $R\subseteq A$ in the detailed definition $R=(G_{R},A)$ with $G_{R}\subseteq A$ .

The zero-digit relations are therefore the subsets of the empty Cartesian product $\textstyle \prod _{i=1}^{0}A_{i}=\{\emptyset \}$ or $A^0 = \{\emptyset\}$ , so $\emptyset$ and $\{\emptyset \}$ , detailed $(\emptyset ,\{\emptyset \})$ and $(\{\emptyset \},\{\emptyset \})$ .

Relations between or on real classes

Often the carrier areas $A_{i}$ a relation are not sets, but real classes, one then speaks of class relations. Occasionally, one can avoid set-theoretical problems arising from this by only considering the graph of the corresponding relation. The (minimal) carrier sets ( $Tr_{i}(R)$ , in the two-digit case definition and value set $Db(R),Wb(R)$ ) are indeed sets, but it is not necessary to commit a priori to source set, target set, ... ( $A,B,A_{i},\dotsc$ ) if the relations are essentially the same. This is not always possible, for example for the equivalence relation of equal power, see also: Cardinal numbers §Definition. Equality of relations in essence is another example.

A two-digit class relation with source class and target class is called predecessor-small if for all $b \in B$ the class of predecessors $\{a\in A\mid aRb\}$ (primal fibre of , see below) is a set (i.e. not a real class). The relation is called English right-narrow if for all $a\in A$ the class of successors $\{b\in B\mid aRb\}$ (image fibre of ) is a set. In the case of right uniqueness (partial mappings, mappings, see below), a class relation is always small, since there is (exactly or at most) one image value for each primal image, so the class of successors is a set of ones (or the empty set). Every injective class mapping is both small and predecessor-small. The containment relation ∈ $\in$ is predecessor-small for any class since the $b \in B$ cannot be real classes but are sets and so $\{a\in A\mid a\in b\}\subseteq b$ also a set. The terms predecessor and successor themselves are usually used in the context of order relations, see order relation §predecessor and successor.

Explanations and spellings

The Cartesian product of two sets and is the set of all ordered pairs of and where any element from the set and one from . In the ordered pair, the order is important, i.e. (a, b) different from (b,a), opposed to the unordered pair $\{a,b\},$ which is identical to $\{b,a\}.$ For $(a,b)\in R$ one also writes $a\;R\;b,$ to make clear that that relation exists between the objects (as in The empty set as a subset of the Cartesian set product taken as a relation is called the null relation $\mathrm {O} :=\emptyset =\{\}$ , the full product is called all-relation (also universal relation) $\mathrm {U}$ (also $\nabla$ called ).

Relations and functions

A function $f\colon A\to B$ is a special, namely a left-stotal and right-unique (two-digit) relation, for more details see below.
A multifunction $f\colon X\multimap Y$ is a left-total relation $f\subseteq A\times B$ .
A partial function $f\colon \;X\rightharpoonup Y$ is a (generally non-left-total) right-unique relation $f\subseteq A\times B$ .

In all cases, $f\subseteq A\times B$ (or $G_{f}\subseteq A\times B$ if the detailed definition is used).

The following applies to functions and multifunctions:

In the more detailed definition $f=(G_{f},A,B)$ because $G_{f}$ is uniquely determined by (linkstotal), also be omitted and more simply $f=(G_{f},B)$ taken.

The following applies to functions and partial functions:

For $(a,b)\in f$ or $(a,b)\in G_{f}$ also write $f\colon a \mapsto b$ (English: maplet), or f(a) = b .

In general:

The zero-digit relations $\mathrm {O} =\emptyset$ (as zero-digit null relations) and $\mathrm {U} =\{\emptyset \}$ (as a zero-digit full relation) have as characteristic functions the Boolean or logical constants ${\mathsf {falsch}}$ and ${\mathsf {wahr}}$ , as always for zero relation and all relation.
The case of single-digit relations is trivial.
relation $R\subseteq A\times B$ (or $R=(G_{R},A,B)$ ) corresponds uniquely to a truth function χ $\chi _{R}\colon \;A\times B\to \{{\mathsf {wahr}},{\mathsf {falsch}}\}$ . This function is also known as the indicator function or characteristic function of the subset $R \subseteq A \times B$ (or $G_{R}\subseteq A\times B$ ), where $\{{\mathsf {wahr}},{\mathsf {falsch}}\}$ $\{1,0\}$ can be replaced by
An -digit relation $R\subseteq A_{1}\times \dotsb \times A_{n}$ (or $R=(G_{R},A_{1},\dotsc ,A_{n})$ ) corresponds to the characteristic function χ $\chi _{R}\colon A_{1}\times \dotsb \times A_{n}\to \{{\mathsf {wahr}},{\mathsf {falsch}}\}.$

It applies:

$n=0\colon \;\chi _{\emptyset }\Leftrightarrow {\mathsf {falsch}},\chi _{\{\emptyset \}}\Leftrightarrow {\mathsf {wahr}}$ .

$n=1\colon \;\chi _{R}(a)\Leftrightarrow a\in R$ .

$n=2\colon \;\chi _{R}(a,b)\Leftrightarrow aRb\Leftrightarrow (a,b)\in R$ .

relation $R\subseteq A\times B$ also be understood as a mapping κ $\kappa _{R}$ from into the power set of κ $\kappa _{R}\colon A\to {\mathcal {P}}(B),\;a\mapsto \{b\in B\mid (a,b)\in R\},$ one then often speaks of a correspondence, and for transition relation.

Concatenation of relations

The forward concatenation of two two-digit relations $R\subseteq A\times B,S\subseteq C\times D$ is defined as follows:

${\begin{array}{lll}R\;\mathbf {;} \;S\equiv RS&:=\{(a,d)\mid \exists b\colon \;aRb\land bSd\}\\&=\{(a,d)\in A\times D\mid \exists b\in B\cap C\colon \;(a,b)\in R\land (b,d)\in S\}.\end{array}}$

Chaining in the reverse order is called backward chaining:

$S\circ R\qquad \quad :=\{(a,d)\in A\times D\mid \exists b\in B\cap C\colon \;(a,b)\in R\land (b,d)\in S\}=R\;\mathbf {;} \;S$ .

Some authors (W. v. O. Quine) use the notation $S\mid R$ an alternative for this.

The sequence is the same for backward chaining as for chaining functions (which can be understood as special relations).

The concatenation of two-digit relations is also called a relative product. In the case of concatenation, the simplest relation, the empty relation contained in every Cartesian product, can also occur. $\emptyset$ (empty set) can occur, namely when and are disjoint, in characters: $B\cap C=\emptyset$ .

Example: The relation "being sister-in-law of" is the union set

of the relative product of the relation "being a brother of" and the relation "being a wife of" and
of the relative product of the relation "being a spouse of" and the relation "being a sister of".

Reverse relation

The inverse relation (also called converse relation, converse or inverse relation) is $R \subseteq A \times B$ defined for a two-digit relation as

${\overset {\smallsmile }{R}}\equiv {}^{\smallsmile }{R}\equiv R^{\sim }\equiv R^{-1}:=\{(b,a)\in B\times A\mid (a,b)\in R\}$ .

Occasionally, this is also called a transposed relation, in characters $R^{T}$ .

Example 1: The inverse relation of the relation "is descendant of" is the relation "is ancestor of".
Example 2: The inverse relation of the relation "is less than" is the relation "is greater than".
Example 3: The inverse relation of the relation "delivers to" is the relation "is delivered by".

The generalisation of the inverse relation (converse) to -digit relations is the permutation of the coordinates of the -tuples contained in it, specifically

the interchanges of only 2 coordinates (transpositions) and
the inversion of the sequence (mirroring),

both examples of (cyclic) self-inverse permutations.

Let π $\pi \colon \{1,2,\dotsc ,n\}\rightarrow \{1,2,\dotsc ,n\}$ be a permutation (i. e. a bijective mapping from $\{1, \dotsc, n\}$ to itself), and let $R\subseteq (A_{i})_{i\in \{1,\dotsc ,n\}}$ an -digit relation, then $S:=\{a\circ \pi \mid a\in R\}$ the relation resulting after applying the permutation π $\pi$ (understand $a=(a_{i})_{i\in \{1,\dotsc ,n\}}$ as a family). In the case of the reflection

$\pi =\sigma _{n}={\begin{pmatrix}1&2&\cdots &n\\n&n-1&\cdots &1\end{pmatrix}}$

$S=\{(a_{n},\dotsc ,a_{1})\mid (a_{1},\dotsc ,a_{n})\in R\}$ .

Image and archetype

Given a two-digit relation $R \subseteq A \times B$ , the image of a set or class set or class

$R^{\to }(X)\equiv R\langle X\rangle :=\{y\mid \exists x\in X\colon \;(x,y)\in R\}$ .

The archetype of a set or class is the set or class

$R^{\leftarrow }(Y)\equiv {\overset {\smallsmile }{R}}\langle Y\rangle \equiv {}^{\smallsmile }{R}\langle Y\rangle \equiv R^{\sim }\langle Y\rangle \equiv R^{-1}\langle Y\rangle =\{x\mid \exists y\in Y\colon \;(x,y)\in R\}$ .

Occasionally, the designation $R{\grave {}}{\grave {}}Y$ (sic!), often also $R[Y]$ written in square brackets as In correspondences, the notation κ $\{a\}$ {\displaystyle $\kappa _{R}(a)=R\langle \{a\}\rangle$ also in use for the image fibre of a singleton { , for which the notation with square brackets is also used in some cases, i.e. $R[a]$ ; in the case of symmetrical relations, i.e. (possibly partial) equivalence or compatibility relations, the notation with square brackets is used. In the case of symmetrical relations, i.e. (partial) equivalence or compatibility relations, the notation $[a]_{R}=R\langle \{a\}\rangle =R^{-1}\langle \{a\}\rangle$ and speaks of equivalence or compatibility or tolerance classes.

Restriction

Relations can be restricted in various ways to subsets of the carrier sets, for more information see Restriction of a relation.

Complementary relation

For two-digit relations $R \subseteq A \times B$ with fixed pre- and post-range A,B the complementary relation is given by

${\overline {R}}\equiv {}^{-}R=(A\times B)\setminus R=\{(x,y)\in A\times B\mid (x,y)\not \in R\}$ ,

analogously for -digit relations $R\subseteq A_{1}\times \dotsb \times A_{n}$ with fixed carrier ranges $A=(A_{1},\dotsc ,A_{n})$ . On the real numbers for example, ≤ {\displaystyle $\mathbb {R}$ is $\leq$ the complementary relation to .

If the complex notation is used as a basis, then $R=(G_{R},A,B)$

${\overline {R}}\equiv {}^{-}R=((A\times B)\setminus G_{R},A,B)$ ,

where A,B are now no longer external additions but components of the relation; analogously for -digit relations in this notation.

As for all sets, the complement is also involutive for relations:

${\overline {\overline {R}}}=R$ .

Homogeneous relations

If A = B so $R\subseteq A\times A$ then the relation is called homogeneous. Some authors already define a general relation as a homogeneous relation, because a general relation $R \subseteq A \times B$ can always be regarded as a restriction of a homogeneous one as well: $R\subseteq (A\cup B)\times (A\cup B)$ .

Special homogeneous relations and operations on homogeneous relations

A special homogeneous relation in a set is the equality or identity relation or diagonal

${\mathrm I}_{A}:=\{(a,b)\in A\times A\mid a=b\}=\{(a,a)\mid a\in A\}.$

Alternative notations for the diagonal are Δ $\Delta _{A}$ or $\mathrm {D} _{A}$ ; if already known, it is simply denoted by ${\mathrm I}$ , Δ {\displaystyle $\Delta$ or $\mathrm D$ designated.

Another special homogeneous relation is the all relation or universal relation

$\mathrm {U} _{A}=A\times A$ (also referred to $\nabla _{A}$ Nabla as ).

If is already known, the index is omitted, as with the identity relation.

The all-relation plays a role in graph theory (see below). An example of its application is the following theorem:

If a directed graph with a set of vertices and an (associated) relation $K\subseteq E\times E$ of edges, then is (strongly) connected if and only if the reflexive-transitive hull of the universal relation.

The formation of the reverse relation (converse relation) of a homogeneous two-digit relation yields again a homogeneous two-digit relation (closedness), twice execution yields again the initial relation (involutivity). The connection of any (also non-homogeneous) relation with its converse relation is symmetrical and reflexive, i.e. an equivalence relation, but generally not equal to the identity relation.

In the case of a homogeneous relation the concatenation $R\subseteq A\times A$ is $R\circ R$ also a homogeneous relation, so that the homogeneous relations in a monoid with the multiplicative link $\circ$ and the neutral element $\mathrm {I} _{A}$ . Thus, $R^{2}:=R\circ R$ and, more generally, powers $R^{n}:=R\circ R^{{n-1}}$ can be defined for $n\in \mathbb {N}$ be defined where _{A}} $R^{0}:=\mathrm {I} _{A}$ $\mathrm {I} _{A}$ is therefore also called a one-relation on the set

Extending the notation instead of $R^{-1}$ ${\overset {\smallsmile }{R}}$ for the inverse relation, one denotes its powers with negative exponents:

$R^{-n}:={\overset {\smallsmile }{R}}^{n}={\overset {\smallsmile }{R^{n}}}$ .

Thus, any integers $n \in \Z$ permissible as exponents.

Moreover, every monoid of homogeneous relations with the empty relation (zero relation) has

$\mathrm {O} =\emptyset$

nor an absorbent element.

By uniting the different powers, the following relations arise

$R^{*}:=\textstyle \bigcup _{n\in {\mathbb {N} _{0}}}R^{n}$ and $R^{+}:=\textstyle \bigcup _{n\in {\mathbb {N} }}R^{n}$ .

Algebraic structures

All together, the two-digit relations on a set form a relation algebra

${\mathfrak {Re}}(A)=(2^{U_{A}},\cap ,\cup ,{}^{-},\mathrm {O} ,U_{A},\circ ,\mathrm {I} _{A},{}^{\smallsmile })$

Using the notations $U_{A}=A^{2}=A\times A,\;\;2^{U_{A}}=2^{A^{2}}={\mathcal {P}}(A\times A)$ .

Together with the constraints, the homogeneous relations form a (heterogeneous) Peirce algebra.

Homogeneous multi-digit relations

Homogeneous multi-digit relations are (with their graph) subsets of $A^{n}$ . For fixed the all-relation $\mathrm {U} _{A}$ (also $\nabla _{A}$ ) and the identity relation (diagonal) $\mathrm {I} _{A}$ (also $\mathrm {D} _{A},\Delta _{A}$ ) given by

$\mathrm {U} _{A}=A^{n},\;\;\mathrm {I} _{A}=\{(a_{i})_{i\in \{1,\dotsc ,n\}}\in A^{n}\mid a_{1}=a_{2}=\dotsb =a_{n}\}$ .

The application of permutations to their -tuples, described as a generalisation of conversation, are of particular importance here, since in this way one always $A^{n}$ remains within the subsets of (closedness). In other words, these operations are bijective mappings in ${\mathcal {P}}(A^{n})=2^{A^{n}}$ . Other notions known from two-digit relations such as reflexivity and symmetry etc. can also be extended in a canonical (natural) way to arbitrary multi-digit relations.

Graph theory and generalisations

→ Main article: Graph theory

Graph theory describes sets with a relation on them together with certain generalisations under a common umbrella term, the graph. The cases considered in graph theory are usually finite (unless otherwise stated).

A relational structure consisting of a set together with a relation on it is called a directed (also oriented) graph $G=(M,R)$ $M=V(G)$ is called the node set of the graph, its elements are called nodes. $E(G)=R$ edge set as a subset of } $M\times M$ , its elements (ordered pairs from ) are called directed (i.e. oriented) edges.

2. symmetric graphs $G=(M,R)$ , i.e. sets with a symmetric relation are equivalent to an undirected graph $G':=(M,\{\{a,b\}\mid a\;R\;b\})$ whose edge set $E(G')$ consists of (undirected) edges, namely the (disordered) sets $\{a,b\}$ with $a\ R\ b$ (here equivalent to $b\ R\ a$ ).

3. further generalisations concern so-called directed graphs with grouped multiple edges, where each edge has a natural number as multiplicity. The edges of such graphs can be represented by a multiset ${\boldsymbol {M}}$ a mapping ${\boldsymbol {M}}=(M,f)$ with a set $M=supp({\boldsymbol {M}})$ and a mapping which $f\colon \;M\to \mathbb {N}$ assigns to f(v) each node $v\in M$ a positive number called colour. Similarly, graphs with coloured nodes and/or edges.

4. weighted nodes and/or edges: We speak of weights instead of colours if the mapping is real-valued. For $f\colon \;M\to [0,1]$ weighted nodes this corresponds to a fuzzy set ${\boldsymbol {M}}=(M,f)$ , for $f\colon \;M\to R^{+}$ is ${\boldsymbol {M}}=(M,f)$ a real valued multiset. The same applies to weighted edges. For oriented graphs, this means in particular that the edge set (a relation, i.e. set of ordered node pairs) becomes a multiset or fuzzy set in an extension of the notion of relation.

Examples

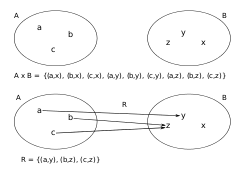
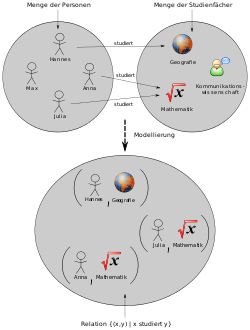
All possible ordered pairs (u,v) with $u\in A:=\{a,b,c\}$ and $v\in B:=\{x,y,z\}$ and a relation defined between and

Example of a relation "A person x studies subject y".

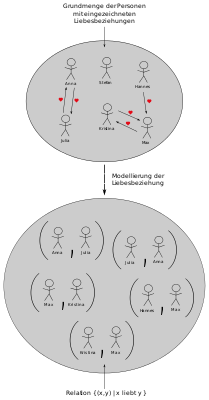
Example of a relation "person x loves person y". This two-digit relation is modelled over a set of ordered pairs.

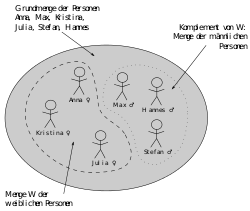
The one-digit relation "person x is female" is modelled as a subset of the basic set.

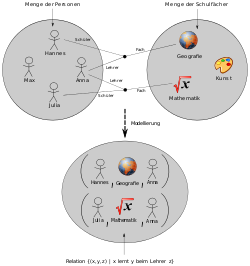
The three-digit relation "Person x learns subject y from teacher z" is realised via a set of 3-tuples.

Properties of two-digit relations

General relations

Overview of the properties

The following relations are important for functions (represented as special relations). In general, the relation exists here $R \subseteq A \times B$ between two different sets A,B, the case A = B course also possible.

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
left total or definal (multifunction)	$\forall a\in A\;\exists b\in {B}\colon \;(a,b)\in R$	${\mathrm I}_{A}\subseteq R^{{-1}}\circ R$	Each element from has at least one partner in
right-total or surjective	$\forall b\in B\;\exists a\in A\colon \;(a,b)\in R$	${\mathrm I}_{B}\subseteq R\circ R^{{-1}}$	Each element from has at least one partner in
left unambiguous or injective	${\begin{aligned}&\forall b\in B\;\forall a,c\in A\colon \\&(a,b)\in R\,\land \,(c,b)\in R\;\Rightarrow \;a=c\end{aligned}}$	$R^{{-1}}\circ R\subseteq {\mathrm I}_{A}$	Each element from has at most one partner in
(right-) unique (partial function)	${\begin{aligned}&\forall a\in A\;\forall b,d\in B\colon \\&(a,b)\in R\,\land \,(a,d)\in R\;\Rightarrow \;b=d\end{aligned}}$	$R\circ R^{{-1}}\subseteq {\mathrm I}_{B}$	Each element from has at most one partner in

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
bitotal	${\begin{aligned}&(\forall a\in A\;\exists b\in B\colon \;(a,b)\in R)\\\land \;&(\forall b\in B\;\exists a\in A\colon \;(a,b)\in R)\end{aligned}}$	${\begin{aligned}&{\mathrm I}_{A}\subseteq R^{{-1}}\circ R\\\land \;&{\mathrm I}_{B}\subseteq R\circ R^{{-1}}\end{aligned}}$	Every element from has at least one partner in and vice versa.
one-to-one	${\begin{aligned}&\forall b,d\in B\;\forall a,c\in A\colon \\&(a,b)\in R\,\land \,(c,b)\in R\;\Rightarrow \;a=c,\\&(a,b)\in R\,\land \,(a,d)\in R\;\Rightarrow \;b=d\end{aligned}}$	${\begin{aligned}&R^{{-1}}\circ R\subseteq {\mathrm I}_{A}\\\land \;&R\circ R^{{-1}}\subseteq {\mathrm I}_{B}\end{aligned}}$	Each element from has at most one partner in and vice versa.
bijective	$\forall b\in B\;\exists !a\in A\colon \;(a,b)\in R$	${\begin{aligned}&{\mathrm I}_{B}\subseteq R\circ R^{{-1}}\\\land \;&R^{{-1}}\circ R\subseteq {\mathrm I}_{A}\end{aligned}}$	Each element from has exactly one partner in
Illustration or function	$\forall a\in A\;\exists !b\in B\colon \;(a,b)\in R$	${\begin{aligned}&\mathrm {I} _{A}\subseteq R^{-1}\circ R\\\land \;&R\circ R^{-1}\subseteq \mathrm {I} _{B}\end{aligned}}$	Each element from has exactly one partner in

Alternative ways of speaking

This article or section needs revision. More details should be given on the discussion page. Please help improve it and then remove this marker.

One also says

left-complete in place of left-total,
right-complete in place of right-total,
preambiguous in place of leftambiguous,
post-unambiguous in place of right-unambiguous,

A right unambiguous or functional relation is also called a partial function. If it is also left-total - i.e. a function - then it is also called a total function for clarification.

Functions

Overview of functional properties for relations

A relation is therefore a (total) function if it is left-total and right-unique. This means that every element in A has exactly one partner in B. The properties surjective, injective and bijective are usually used for functions and specify certain additional properties. For example, a function (and also any relation) is bijective if it is surjective and injective, i.e. if its inverse relation $R^{-1}$ a function.

The relation is called	exactly when they have a	is or equivalent (quantity notation)	and that means:
Surjection	surjective function	${\begin{aligned}&{\mathrm I}_{A}\subseteq R^{{-1}}\circ R\\\land \;&R\circ R^{{-1}}={\mathrm I}_{B}\end{aligned}}$	Each element from has exactly one partner in and each element from has at least one partner in
Injection	injective function	${\begin{aligned}&\mathrm {I} _{A}=R^{-1}\circ R\\\land \;&R\circ R^{-1}\subseteq \mathrm {I} _{B}\end{aligned}}$	Each element from has exactly one partner in and each element from has at most one partner in
Bijection	bijective function	${\begin{aligned}&\mathrm {I} _{A}=R^{-1}\circ R\\\land \;&R\circ R^{-1}=\mathrm {I} _{B}\end{aligned}}$	Each element from has exactly one partner in and vice versa.

Reverse function

A mapping or function is also called

reversible uniquely or reversible if it is bijective.

A function is always invertible as a relation, but as a function it is invertible exactly when its inverse relation is also a function, i.e. when there is an inverse function of it.

Homogeneous relations

The examples given in the following tables refer to the ordinary arrangement of real numbers when using the equals sign "=", the less-than sign "<" and the less-than-equal sign "≤".

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
Right-comparative or third-comparative	${\begin{aligned}&\forall a,b,c\in A\colon \\&(a,c)\in R\,\land \,(b,c)\in R\\&\Rightarrow \;(a,b)\in R\end{aligned}}$	$R^{{-1}}\circ R\subseteq R$	If two elements are each related to an identical third element, then they are also related to each other. E.g. with and always
left-hand comparative or Euclidean	${\begin{aligned}&\forall a,b,c\in A\colon \\&(a,b)\in R\,\land \,(a,c)\in R\\&\Rightarrow \;(b,c)\in R\end{aligned}}$	$R\circ R^{{-1}}\subseteq R$	If a first element is related to a second and a third element, these are also related to each other. For example, with and always applies as well $b=c.$
transitive	${\begin{aligned}&\forall a,b,c\in A\colon \\&(a,b)\in R\,\land \,(b,c)\in R\\&\Rightarrow \;(a,c)\in R\end{aligned}}$	$R\circ R\subseteq R$	If a first element is related to a second element and this in turn to a third element, the first element is also related to the third element. For example, < c result in a < . $a<c.$
intransitive	$\begin{align} &\forall a,b,c \in A\colon\\ &(a,b) \in R \,\land\, (b,c) \in R\\ &\Rightarrow\; (a,c) \notin R\\ \end{align}$	$(R\circ R)\cap R=\emptyset$	If two elements are in relation and, in addition, the second element is in relation to a third element, then the first element is not in relation to the third element. For example, any natural number is the (immediate) predecessor of and the (immediate) predecessor of $n+2,$ but is not the (immediate) predecessor of $n+2.$

Non-transitivity (i.e. the relation is not transitive), intransitivity and negative transitivity are each different from each other.

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
reflexive	$\forall a\in A\colon (a,a)\in R$	${\mathrm I}\subseteq R$	Each element is in relation to itself, e.g. $a\leq a.$
reflexive	$\forall a\in A\colon (a,a)\in R$	${\mathrm I}\cap R={\mathrm I}$	Each element is in relation to itself, e.g. $a\leq a.$
irreflexive	$\forall a\in A\colon (a,a)\notin R$	${\mathrm I}\cap R=\emptyset$	No element is in relation to itself, e.g. applies to $a<a$ no a .

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
symmetrical	${\begin{aligned}&\forall a,b\in A\colon \\&(a,b)\in R\;\Rightarrow \;(b,a)\in R\end{aligned}}$	$R^{{-1}}\subseteq R$	The relation is undirected, e.g. from always follows $b=a$ (and vice versa)
symmetrical		$R^{{-1}}=R$
antisymmetrical or identitive	$\begin{align} &\forall a,b \in A\colon\\ &(a,b) \in R \,\land\, (b,a) \in R\\ &\Rightarrow\; a = b \end{align}$	$R^{{-1}}\cap R\subseteq {\mathrm I}$	There are no two different elements that are related in both directions, e.g. it $b\leq a$ always follows from $a\leq b$ and
asymmetric	$\begin{align} &\forall a,b \in A\colon\\ & (a,b) \in R \;\Rightarrow\; (b,a) \notin R \end{align}$	$R^{{-1}}\cap R=\emptyset$	There are no two elements that are related in both directions, e.g. it follows from b < a

The relation is called	exactly when (predicate logic)	or equivalent (quantity notation)	and that means:
total or complete	$\begin{align} &\forall a,b \in A\colon\\ &(a,b) \in R \,\lor\, (b,a) \in R \end{align}$	$R^{{-1}}\cup R=A\times A$	Two elements each are in relation, e.g. if $a\leq b$ or always $b\leq a$ holds.
Connected	$\begin{align} &\forall a,b \in A\colon\\ &a \neq b\\ &\Rightarrow\; (a,b) \in R \,\lor\, (b,a) \in R \end{align}$	$R^{{-1}}\cup R\cup {\mathrm I}=A\times A$	Two different elements are related, e.g. if $a=b,$ < a $b<a,$ if a ≤ b {\displaystyle $a\leq b$ {\displaystyle
trichotome	$\begin{align} &\forall a,b \in A\colon\\ &((a,b)\in R \Rightarrow (b,a) \notin R) \,\land\\ &(a \neq b\\ &\Rightarrow\; (a,b) \in R \,\lor\, (b,a) \in R) \end{align}$	${\begin{aligned}R^{-1}\cup R\cup \mathrm {I} &=A\times A\\\land \;R^{-1}\cap R&=\emptyset \end{aligned}}$	Two different elements are always related in exactly one way, e.g. if either < a always

The following relationships apply between the properties:

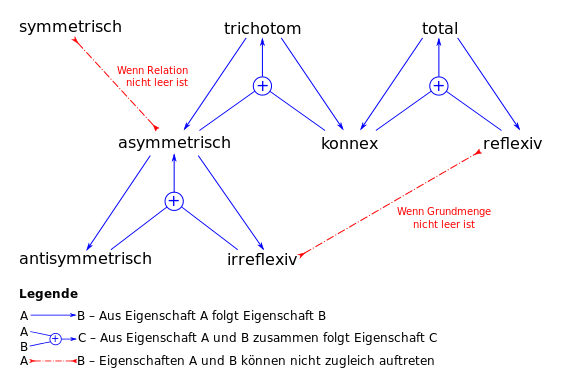
Zusammenhang der Eigenschaften binärer Relationen

The following relationships exist between the properties of a relation and those of its complement ${\overline {R}}$

is reflexive $\iff$ ${\overline {R}}$ is irreflexive (and vice versa).
is symmetrical $\iff$ ${\overline {R}}$ is symmetrical.
is antisymmetric $\iff$ ${\overline {R}}$ is connex (and vice versa).
is total $\iff$ ${\overline {R}}$ is asymmetric (and vice versa).

Relation classes

Other important classes of relations and their properties:

Quasi-order or pre-order: transitive and reflexive
Compatibility relation or tolerance relation: compatible (reflexive and symmetrical) (English: in the finite case dependency relation, in the transfinite case tolerance relation).
Equivalence relation: transitive, reflexive and symmetrical
Half-order/partial order, partial order or order: transitive, reflexive and antisymmetrical.
Full order/total order or linear order: transitive, reflexive, antisymmetrical and total
Well-ordering: a linear ordering in which every non-empty subset of A has a smallest element.
Strict order or strict half order/partial order: transitive, irreflexive and antisymmetrical (i.e. asymmetrical)
Strict full order/total order or linear strict order: transitive, irreflexive, antisymmetrical and connective

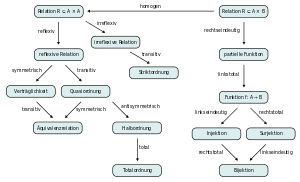
Relationships between different two-digit relations

Relation sign

In elementary mathematics there are three basic comparative relations:

(Example: $2<3,$ is smaller than 3")
(Example: $3=3,$ "3 is equal to 3")
(Example: $3>2,$ is greater than 2")

with $x,y\in \mathbb{R}$ .

Two real numbers always stand in exactly one of these relations to each other. These relation signs can also be used to form others. The following applies:

$x \leq y$ if = y (Example: $4\leq 5,$ "4 is not greater than 5")
$x\geq y$ if = y (Example: $5\geq 5,$ "5 is not less than 5")
$x\neq y$ if > y (Example: $4\neq 5,$ "4 is not equal to 5")

for all $x,y\in \mathbb{R}$ .

The above order relations do not exist for complex numbers.

Mathematicians also use the sign ≤ for abstract order relations (and ≥ for the associated inverse relation) while "<" is not an order relation in the sense of the mathematical definition.

For equivalence relations, "symmetrical" symbols such as ≈, ~, ≡ are preferred.

Category theory

For any half-ring $(H,+,\cdot )$ with zero element $0$ and one element following ${\mathcal {C}}$ is a category:

${\mathrm {Ob}}({\mathcal C})={\mathrm {Ob}}({\mathbf {Set}})$ .
A morphism $f\in {\mathrm {Hom}}_{{{\mathcal C}}}(X,Y)$ is a function $f\colon X\times Y\to H$ .
For objects following applies

This is identical to the Kronecker : $\mathrm {id} _{X}(x,x')=\delta _{xx'}$ .

For objects and morphisms $f\in \mathrm {Hom} _{\mathcal {C}}(Y,Z),\ g\in \mathrm {Hom} _{\mathcal {C}}(X,Y)$ holds.

$(f\circ g)(x,z):=\sum _{{y\in Y}}g(x,y)\cdot f(y,z)$ .

The morphisms are thus set-indexed matrices and their composition occurs as in matrix multiplication, $\mathrm {id} _{x}$ corresponds to the unit matrix .

In the special case $(H,+,\cdot )=(\{0,1\},\lor ,\land )$ applies. ${\mathcal C}={\mathbf {Rel}}$ i.e., ${\mathcal {C}}$ is the category of relations.

Application

Operations on whole relations are studied in relational algebra. In computer science, relations are important when working with relational databases.

Finitary relation

Definitions

Two-digit relation

n-digit relation

Relations between or on real classes

Explanations and spellings

Relations and functions

Concatenation of relations

Reverse relation

Image and archetype

Restriction

Complementary relation

Homogeneous relations

Special homogeneous relations and operations on homogeneous relations

Algebraic structures

Homogeneous multi-digit relations

Graph theory and generalisations

Examples

Properties of two-digit relations

General relations

Overview of the properties

Alternative ways of speaking

Functions

Overview of functional properties for relations

Reverse function

Homogeneous relations

Relation classes

Relation sign

Category theory

Application

See also

Search by letter