Regular polygon

A regular polygon, regular polygon, regular polygon, regular polygon or isogon (from Greek ἴσος, equal and γωνία, angle) is, in geometry, a plane polygon that is both equilateral and equiangular. Thus, for a regular polygon, all sides are equal in length and all interior angles are equal in size. The corners of a regular polygon all lie on a common virtual or real circle, with adjacent corners appearing at the same central angle.

Regular polygons can be simple or overlapped. Simple regular polygons are always convex. Overlapped regular polygons are called regular asterisk polygons. The symmetry group of a regular -corner is the dieder group , consisting of exactly rotations and reflections.

All parameters of regular polygons, such as the length of the diagonals, the perimeter or the area, can be specified using trigonometric functions. However, not all regular polygons can be constructed with compass and ruler. Regular polygons are used, among other things, in the approximation of the circle number π , for parquetry, in architecture, and as a coin shape.

Definition

A polygon with sides and interior angles α is called regular if

and α

holds. Thus, in a regular polygon, all sides are congruent to each other and all angles are equal.

Classification

A distinction is made between simple and overlapped regular polygons. All simple regular polygons with the same number of vertices are similar to each other and are denoted in combinatorial geometry by the Schläfli symbol To exclude degenerate cases, is usually assumed. The first simple regular polygons are:

• the equilateral triangle ,
• the square ,
• the regular pentagon and
• the regular hexagon .

Overlapped regular polygons are called regular star polygons and have a greater variety of shapes. They are denoted by the Schläfli symbol , where is the orbital number of the polygon about its center. The orbital number must be divisor invariant to , otherwise the polygon degenerates. The first regular star polygons are

• the five star ,
• the seven-pointed stars and and
• the eight-pointed star .

Thus, the number of different types of regular polygons with vertices is , where φ {\displaystyleis the Eulerian phi function. If and are not divisor-aligned, the Schläfli symbol denotes stars composed of multiple regular polygons. Examples are the hexagram and the octagram .

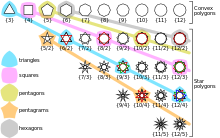
Designations of regular polygons and other star shapes