Reflexive relation

The reflexivity of a two-digit relation on a set is given if $xRx$ holds for all elements the set, i.e. each element is in relation to itself. Then called reflexive.

A relation is called irreflexive if the relation $xRx$ does not hold for any element of the set, i.e. no element is in relation to itself. There are also relations that are neither reflexive nor irreflexive if the relation holds $xRx$ for some elements of the set, but not for all.

Reflexivity is one of the conditions for an equivalence relation or an order relation; irreflexivity is one of the conditions for a strict order relation.

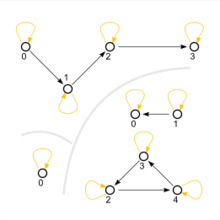
Three reflexive relations, represented as directed graphs

Formal definition

If a set and $R\subseteq M\times M$ a two-digit relation on , then one defines (using infix notation):

is reflexive : $\Longleftrightarrow \forall x\in M:xRx$

is irreflexive : $\Longleftrightarrow \forall x\in M:\neg \ xRx$

Examples

Reflexive

The less than or equal relation ≤ $\leq$ on the real numbers is reflexive, since always $x\leq x$ holds. Moreover, it is a total order. The same holds for the relation ≥ $\geq$ .

The ordinary equality on the real numbers is reflexive, since always holds. Moreover, it is an equivalence relation.

The subset relation $\subseteq$ between sets is reflexive, since always $A\subseteq A$ holds. Moreover, it is a half-order.

Irreflexive

The Kleiner relation on the real numbers is irreflexive, since never holds. Moreover, it is a strict total order. The same is true for the relation .

The inequality $\ne$ on the real numbers is irreflexive, since never $x\neq x$ holds.

The real subset relation $\subset$ between sets is irreflexive, since never $A\subset A$ holds. Moreover, it is a strict half-order.

Neither reflexive nor irreflexive

The following relation on the set of real numbers is neither reflexive nor irreflexive:

$xRy:\Longleftrightarrow y=x^{2}$

Reason: For holds xRx , for holds ¬ $\neg xRx$ .