Recursion

This article is about the basic process of recursion: example of application is the recursive definition in mathematics; for the term recursive set, see Decidable.

A recursion (Latin recurrere 'to run back') is a basically infinite process that contains itself as a part or can be defined with the help of itself. Usually, recursive processes can be described relatively briefly or can be triggered by a relatively short instruction. In recursion, the successive sub-processes or the successively generated objects are not independent of each other, but there is a special, the recursive relationship between each pair of steps or pair of objects.

"The term [recursion] is very comprehensive". In nature, it is a frequently observable process (e.g., in plant growth). In many areas of culture, it is replicated, such as in the fine arts, where the phenomenon is referred to as mise en abyme, among other things. In mathematics and computer science, recursion is a common term.

Recursion is also a problem-solving strategy. Complex issues can often be captured very elegantly with recursively formulated rules. The basic principle is the reduction of a general task to a simpler task of the same class. Among other things, this is also used in so-called recursive programming: In order for recursion to occur, a procedure, function, or method need only call itself. This process continues until a termination condition contained in the program takes effect.

In mathematics, recursive formulation is used with advantage to explain functions (see Recursive Definition).

Infinite reflection as an example of recursion: The person sits facing a larger wall mirror with the mirror held up. The following mirror image contains itself as a part.

Introductory examples for recursion

Recursive graphics

Recursive rules can also be used in the creation of graphics, this results in the so-called fractals - aesthetically pleasing, natural-looking structures. An example is the Pythagorean tree. It is created according to the following rule (the third step shows the recursion):

Build a square on a given baseline.
On its top draw a triangle with given angles or height.
Apply the two steps above again to the two free sides of the newly created triangle.

This algorithm is then unfolded to a given recursion depth: If it is run once, the result is a triangle with a square over each of the three sides. This looks like an illustration of the Pythagorean theorem - hence the name. The greater the recursion depth, the more the structure resembles a tree.

You can skip the first two steps in the above description and start the recursive process with the illustration for the Pythagorean Theorem:

Create two more similar illustrations from this illustration, each with a large square identical to one of the two small squares in the previous illustration.
Create two more similar illustrations from each of the illustrations created in the first step, following the same procedure, and so on.

Recursion in grammar

In linguistics, the grammar of natural languages is described, among other things, with the help of so-called phrase structure rules. According to most linguists, all human languages show the property of being recursively structured (in contrast to signal systems in the animal kingdom). This arises because in the decomposition of a grammatical unit labelled with a category, the same category may reappear. An example is the phenomenon of subordinate clauses, which is described here with the following highly simplified production rule:

S → NP VP (a sentence consists of a nominal phrase (as subject) and a verbal phrase).
VP → V NP* (a verb phrase consists of a verb and zero to many nominal phrases as objects of the verb).
VP → V S (a verb phrase consists of a verb and a subordinate clause as the object of the verb).

This grammar leaves the choice whether the spelling out of "VP" should be done with rule 2 or 3. In the case that steps 1 and then 3 are called, a recursion results: The symbol S appears as the product of rule 3, which in turn represents the start for rule 1.

Recursion in mathematics

Recursion plays a major role in mathematics, for example in the recursive definition of functions. As examples, the calculation of the factorial and the Fibonacci sequence are presented below. However, recursion methods and recursive definition are not limited to functions of natural numbers in mathematics.

Faculty

The function factorial of a natural number $n\geq 1$ is defined as the product of the numbers 1 to :

$n!=1\cdot 2\cdot 3\dotsm n=\prod _{k=1}^{n}k$

Examples

${\begin{array}{rll}1!&=1&=1\\2!&=1\cdot 2&=2\\3!&=1\cdot 2\cdot 3&=6\\4!&=1\cdot 2\cdot 3\cdot 4&=24\\\end{array}}$

If this list is to be continued, the recursiveness almost results by itself. For the calculation of 5! one will not start from the beginning, but can fall back on previous results, i.e.

$5!=4!\cdot 5=120$

Generalized, the function can thus be defined recursively:

$n!=\left\{{\begin{matrix}1&&{\text{falls }}n=1&&{\text{(Rekursionsanfang)}}\\(n-1)!\cdot n&&{\text{sonst}}&&{\text{(Rekursionsschritt)}}\end{matrix}}\right.$

The Fibonacci sequence

A classic example of a recursive function is the Fibonacci sequence, where each successive element of the sequence is the sum of the previous two:

$0,1,1,2,3,5,8,13,21,34,\dotsc$

Unlike the factorial function, there is no trivial closed representation here. The simplest description is the recursive definition:

$\operatorname {fib} (n)=\left\{{\begin{matrix}0&&{\text{falls }}n=0&&{\text{(Rekursionsanfang)}}\\1&&{\text{falls }}n=1&&{\text{(Rekursionsanfang)}}\\\operatorname {fib} (n-1)+\operatorname {fib} (n-2)&&{\text{sonst}}&&{\text{(Rekursionsschritt)}}\end{matrix}}\right.$

This recursive definition is cascading. The third Fibonacci number is calculated using this definition as follows:

${\begin{matrix}\operatorname {fib} (3)&=&\operatorname {fib} (2)+\operatorname {fib} (1)&{\text{(Rekursionsschritt)}}\\&=&\operatorname {fib} (1)+\operatorname {fib} (0)+\operatorname {fib} (1)&{\text{(Rekursionsschritt)}}\\&=&1+\operatorname {fib} (0)+\operatorname {fib} (1)&{\text{(Rekursionsanfang)}}\\&=&1+0+\operatorname {fib} (1)&{\text{(Rekursionsanfang)}}\\&=&1+0+1&{\text{(Rekursionsanfang)}}\\&=&2\end{matrix}}$

The calculation for $\operatorname {fib} (1)$ is performed multiple times here. This suggests that there is potential for optimization.

Pythagorean tree

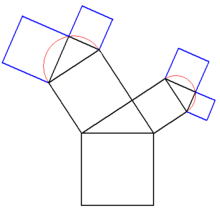
"Sprouting" Pythagorean tree

Formal types of recursion

The most common form of recursion is linear recursion, in which at most one recursive call may occur in each case of the recursive definition. The calculation then runs along a chain of calls. In such a recursion, the call tree therefore contains no branches.

The primitive recursion is a special case of the linear recursion, which can always be replaced by an iteration (see below #On the relation of recursion and iteration). Here one defines functions on the natural numbers, where in each recursive call its first parameter decreases or increases by one. Each primitive-recursive definition can be replaced by a loop (e.g. For-loop or While-loop) with the help of a stack.

Terminal or repetitive recursion (tail recursion or end recursion) refers to the special case of linear recursion in which each recursive call is the last action of the recursive call. Tail recursion can be replaced by while loops and vice versa. (In contrast to end recursion is head recursion; see under Infinite Recursion).

Nested recursion is recursion in which recursive calls occur in parameter expressions of recursive calls. This form of recursion is considered to be extremely difficult to understand.

Cascading recursion refers to the case in which several recursive calls are adjacent to each other. The recursive calls then form a tree. Cascading recursion is considered elegant, but without further action it can result in an exponential computational cost. It is often used as a starting point for deriving another more efficient formulation.

Reciprocal recursion refers to the definition of multiple functions by using them reciprocally from each other. It can be traced back to the ordinary recursion of a tuple-valued function.