Multiplicative inverse

The reciprocal (also the reciprocal value or reciprocal) of a number {\displaystyle 0}other than xis, in arithmetic, that number which, when xmultiplied by 1, gives the number ; it is notated as \tfrac{1}{x}or . x^{-1}

Properties

The closer a number is to {\displaystyle 0}, the farther its reciprocal is from {\displaystyle 0}. The number {\displaystyle 0}itself has no reciprocal and is not a reciprocal. The reciprocal y=f(x)={\tfrac 1x}function described by (see figure) has a pole there. The reciprocal of a positive number is positive, the reciprocal of a negative number is negative. This finds its geometric expression in the fact that the graph decomposes into two hyperbolic branches, which lie in the first and third quadrants, respectively. The reciprocal function is an involution, that is, the reciprocal of the reciprocal of xis again x.If a quantity yis inversely proportional to a quantity x,then it is proportional to the reciprocal of x.

The reciprocal of a fraction, that is, the reciprocal of a quotient {\tfrac ab} with a,b\neq 0, is obtained by interchanging the numerator and denominator:

{\displaystyle {\frac {1}{\frac {a}{b}}}={\frac {b}{a}}}

From this follows the calculation rule for dividing by a fraction: Dividing by a fraction is done by multiplying by its reciprocal. See also fraction calculation.

The inverse {\tfrac 1n}of a natural number nis called a root fraction.

Also, to every complex number {\displaystyle 0}different from z=a+b{\mathrm i}with real numbers a,bthere is a reciprocal {\tfrac {1}{z}}.With the absolute value |z|={\sqrt {a^{2}+b^{2}}}of zand the complex number zzconjugate to \overline {z}=a-b{\mathrm i}holds:

{\frac {1}{a+b{\mathrm i}}}={\frac {1}{z}}={\frac {\overline {z}}{z\overline {z}}}={\frac {\overline {z}}{|z|^{2}}}={\frac {a-b{\mathrm i}}{a^{2}+b^{2}}}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}{\mathrm i}

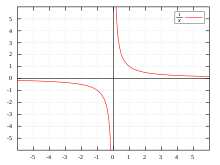
The graph of the reciprocal function is a hyperbola.Zoom
The graph of the reciprocal function is a hyperbola.

Examples

  • The reciprocal of 1is again 1.
  • The reciprocal of {\displaystyle 0{,}001}is 1000.
  • The reciprocal of 2is {\displaystyle {\tfrac {1}{2}}=0{,}5}.
  • The reciprocal of the fraction {\tfrac {2}{5}}is {\displaystyle {\tfrac {5}{2}}=2{\tfrac {1}{2}}=2{,}5}.
  • The inverse of the complex number 3+4{\mathrm i}is {\tfrac {1}{3+4{\mathrm i}}}={\tfrac {3}{25}}-{\tfrac {4}{25}}{\mathrm i}.

AlegsaOnline.com - 2020 / 2023 - License CC3