Rayleigh scattering

Rayleigh scattering [ˈreɪlɪ-], named after John William Strutt, 3rd Baron Rayleigh, refers to the (mainly) elastic scattering of electromagnetic waves by particles whose diameter $\lambda$ is small compared to the wavelength λ , for example in the scattering of light by small molecules. In the case of scattering in the Earth's atmosphere from molecular oxygen and nitrogen, the inelastic component due to rotational Raman scattering is typically also counted as part of Rayleigh scattering, since this only causes a shift in the wavenumber of the photon of less than 50 cm-1. The effective cross section of this contribution has the same wavelength dependence as the elastic component.

The scattering cross section σ $\sigma$ of Rayleigh scattering is proportional to the fourth power of the frequency of the electromagnetic wave. This is true not only for independently scattering particles, i.e., at particle distances greater than the coherence length of the radiation, but also at higher particle concentrations for scattering from inhomogeneities of the refractive index due to a statistical arrangement of the particles, for example, in gases or glasses. Blue light has a higher frequency than red light and is therefore more strongly scattered.

The frequency-dependent scattering of sunlight at the particles of the earth's atmosphere causes the sky blue during the day, and the morning redness as well as the evening redness during twilight. Standing close above the horizon, the moon also appears reddish.

Rayleigh scattering occurs because the incident light excites the electrons of a molecule and ${\vec {p}}_{{\text{ind}}}=\alpha {\vec {E}}$ induces a dipole moment which oscillates in the same way as the incident electromagnetic radiation. The induced dipole moment now acts like a Hertzian dipole and emits light that has the same wavelength as the incident light.

Rayleigh-scattered light is polarized, especially strongly at scattering angles of 90°. The left image is taken without, the right one with a polarizing filter in blocking direction.

Rayleigh scattering is the cause of aerial perspective

Rayleigh scattering causes the blue hue of the sky during the day and the red hue of the sun when it sets or rises.

The waxing crescent moon also appears reddish when it is only a few degrees above the horizon. The moonlight now reaches the observer only after a longer passage of more than 200 kilometres through the Earth's atmosphere.

Cross section

The effective cross section σ $\sigma$ of Rayleigh scattering for a single particle is obtained from the oscillator model. In the limiting case of low frequencies (compared to the natural frequency, ω $\omega \ll \omega _{0}$ ) holds:

$\sigma (\omega )\approx \sigma _{{\mathrm {Th}}}{\frac {\omega ^{4}}{\omega _{0}^{4}}}$

Where σ $\sigma _{{\mathrm {Th}}}=0{,}665\cdot 10^{{-24}}\,{\mathrm {cm}}^{2}$ the Thomson effective cross section. The angular distribution and polarization is that of a dipole in the direction of the incident wave.

If there are several particles in the coherence volume, the scattered waves interfere. When there are many particles per coherence volume, spatial variations of the refractive index act as scattering centers. Thus, for a sphere with diameter $d\ll {\tfrac {\lambda }{2\pi }}={\tfrac {1}{k}}$ and refractive index $n_{2}$ in a medium $n_{1}$ is the scattering cross section:

$\sigma ={\frac {8\pi d^{6}k^{4}}{3}}\left({\frac {\left({\frac {n_{2}}{n_{1}}}\right)^{2}-1}{\left({\frac {n_{2}}{n_{1}}}\right)^{2}+1}}\right)^{2}.$

Milky opal is red-orange in transmission because density inhomogeneities scatter the blue light laterally.

The blue respectively the red of the sky

Rayleigh scattering explains why the sky appears blue. The wavelength of blue light, λ $\lambda _{{\mathrm {blau}}}$ , is about 450 nm, and that of red light is about 650 nm. Thus it follows for the ratio of the effective cross sections:

${\begin{aligned}{\frac {\sigma _{\text{blau}}}{\sigma _{\text{rot}}}}&={\frac {\frac {1}{\lambda _{\text{blau}}^{4}}}{\frac {1}{\lambda _{\text{rot}}^{4}}}}=\left({\frac {650\,{\text{nm}}}{450\,{\text{nm}}}}\right)^{4}\approx 4{,}4\end{aligned}}$

In the picture, the radiated power distribution of the sun, approximated by Planck's radiation law from a surface temperature of 5777 K, is drawn in red. The spectral maximum is then at green light (500 nm wavelength). The spectral maximum of daylight, on the other hand, is at 550 nm, partly due to the scattering effect described here. The power distribution of the scattered light (blue curve) is obtained by multiplying by ω4. According to this, the maximum moves far into the UV range. In fact, however, it lies in the near UV, since molecular absorptions are added at shorter wavelengths.

During the day, when the sun is high in the sky, the light only travels a short distance through the atmosphere. In the process, only a little blue light is scattered in other directions. This is why the sun appears yellow. From high-flying aircraft, the sun appears "whiter" because less blue light has been scattered away.
The sum of all scattered light makes the sky appear blue from all other directions. On the moon, however, where there is no dense atmosphere, the sky appears black even during the day.
When the sun is low, the path of sunlight through the earth's atmosphere is much longer. As a result, a large proportion of the high-frequency light components (blue) are scattered to the side, light with long wavelengths predominantly remains and the colour impression of the sun shifts towards red. This effect is further enhanced by additional particles in the air (e.g. haze, aerosols, dust). However, Chappuis absorption is responsible for the blue colouring of the sky at the zenith after sunset, which is hardly noticeable at higher sun elevations.

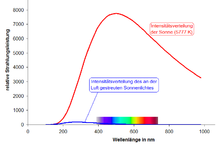
Power distribution of scattered sunlight

Rayleigh scattering

Cross section

The blue respectively the red of the sky

Search by letter