Rational number

$\mathbb {Q}$

A rational number is a real number that can be represented as a ratio (Latin ratio) of two integers. To denote the set of all rational numbers, the formula symbol $\mathbb {Q}$ (Unicode U+211A: ℚ) is used (from "quotient", see letter with double bar). It includes all numbers that can be represented as a fraction containing integers in both the numerator and denominator. The exact mathematical definition is based on equivalence classes of pairs of integers.

The rational numbers are also called fractions in school mathematics. Through the introduction of the fractions, the division becomes feasible even if, for example, the dividend is smaller than the divisor. For example, the division task 3 : 4 = ? is not solvable within the natural or whole numbers.

For example, the fraction ^{3⁄4 represents:}

the division 3 : 4 (3 divided into 4, 3 divided into 4, 3 divided into 4s, 3 divided into 4 (equal) parts, 3 divided by 4),
the result of the division as its own (fractional) number ^3⁄4 (three quarters),
the order: "Divide into 4 parts, take 3" (three out of four (parts)).

The terms ordinary fraction, root fraction, real fraction, I, improper fraction, I, truncated fraction, expanded fraction, decimal fraction, binary fraction ... on the other hand, are used for special notations or forms of rational numbers. The decimal fraction expansion of a rational number is periodic.

A real number that is not a rational number is called an irrational number. This includes, for example, ${\sqrt {2}}$ , π $\pi$ , ${\mathrm e}$ and $\Phi$ . The decimal fraction expansion of an irrational number is not periodic.

Since the rational numbers form a countable set, but the real numbers form a supra-countable set, "almost all" real numbers are irrational.

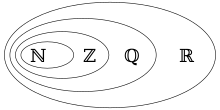
The rational numbers (ℚ) are part of the real numbers (ℝ). They themselves include the integers (ℤ), which in turn include the natural numbers (ℕ).

Definition

The set of rational numbers consists of the set of negative rational numbers, the number zero and the set of positive rational numbers. The definition of rational numbers is based on the representation of rational numbers by fractions, i.e. pairs of integers. It is constructed in such a way that arithmetic with rational numbers can be performed as usual using their fraction representations, but at the same time abstracts the rational number from its fraction representations. The rational numbers are not postulated as completely new things, but are traced back to the integers.

The definition starts with the set of all ordered pairs (a,b) integers with $b\not =0$ . Important: These pairs are not the rational numbers.

One defines addition and multiplication on this set as follows:

$(a,b)+(c,d):=(a\cdot d+b\cdot c,\,b\cdot d)$

$(a,b)\cdot (c,d):=(a\cdot c,\,b\cdot d)$

These are the well-known calculation rules of the fraction calculation. The pairs of numbers can be understood as fractions.

One goal of the definition of rational numbers is that, for example, the fractions 2/3 and 4/6 denote the same "number". Thus, one considers fractions that are equivalent (of the same value) to each other. This is expressed by an equivalence relation, which is defined as follows:

$(a,b)\sim (c,d)\;:\!\iff a\cdot d=b\cdot c\;$ .

It is important that this relation is actually an equivalence relation, i.e. that it decomposes the total set into subsets (here called equivalence classes) of mutually equivalent elements; this can be proved.

For the equivalence classes one defines again calculation rules which are based on the fraction calculus and ensure that what one understands by a rational number is abstracted from the concrete fraction representation. The addition $q+r=:s$ of the equivalence classes and is defined as follows:

From chooses any element, i.e. an ordered pair (a,b) integers (thus one chooses a single element of and not two). Similarly, from chooses the element (c,d) .

(a,b) and (c,d) now added according to the fraction calculus and a pair obtained (e,f) . This is an element of an equivalence class which is the result of the addition.

It is important to note that regardless of the concrete choice of $(a,b)\in q$ and $(c,d)\in r$ always an element of one and the same equivalence class $s\ni (e,f)$ , emerges; this property of addition, its well-definiteness, must and can be proved.

Analogously, the multiplication is $q\cdot r=t$ defined.

The equivalence classes $q,r,s,t$ are taken to be elements of a new set $\mathbb {Q}$ and call them rational numbers. A single rational number $q\in \mathbb {Q}$ is thus an infinite set of ordered pairs (a,b) . This set is very often $(a,b)=:{\tfrac {a}{b}}=:a/b$ written as a fraction which is the equivalence class

${\frac {a}{b}}:={\bigl \{}(c,d)\;{\big |}\;c\in \mathbb {Z} \;\wedge \;d\in \mathbb {Z} \setminus \{0\}\;\wedge \;(c,d)\sim (a,b){\bigr \}}$

of all (a,b) pairs equivalent to The horizontal or (from top right to bottom left) oblique separator between the two integers is called the fraction bar. The first named integer is the numerator, the second the denominator of the fraction. The denominator is always different from $0$ and can be $(a,b)\sim (-a,-b)$ positive because of The preferred representation of the rational number ${\tfrac {a}{b}}$ is the (maximally) truncated fraction

${\frac {c}{d}}\;:=\;{\frac {a\div e}{b\div e}}$

with

$e:=\operatorname {sgn}(b)\cdot \operatorname {abs} {\bigl (}\operatorname {ggT} (a,b){\bigr )}$ ,

where $\operatorname {ggT} (a,b)$ stands for the greatest common divisor of and Thus the equivalence class ${\tfrac {a}{b}}$ consists exactly of the pairs of integers

${\bigl \{}(c\cdot f,d\cdot f)\;{\big |}f\in \mathbb {Z} \setminus \{0\}{\bigr \}}$ .

Identifying the integer $n\in \mathbb{Z }$ with the rational number ${\tfrac {n}{1}}\in \mathbb {Q}$ , then one has a number expansion of the integers, which is also called the formation of the quotient body. If and are two integers and s=n+m , $p=n\cdot m$ their sum and product, the calculation rules for fractions are just such, that ${\tfrac n1}+{\tfrac m1}={\tfrac s1}$ and ${\tfrac n1}\cdot {\tfrac m1}={\tfrac p1}$ holds. Moreover, by virtue of this identification, a fraction is in fact the quotient of numerator and denominator. In this sense, the fraction stroke is also $\div$ used as an ordinary division sign instead of ÷

Order relation

One defines

${\frac {a}{b}}<{\frac {c}{d}}\qquad :\Longleftrightarrow \qquad a\operatorname {sgn}(b)\operatorname {abs} (d)<\operatorname {abs} (b)c\operatorname {sgn}(d)$

with the well-known comparison characters functions sgn {\displaystyle $\sgn$ abs {\displaystylebased on the ordering of the integersThis definition is independent of truncation or expansion of fractions, since they always affect both sides of the right -character. With $b=\operatorname {sgn}(b)=\operatorname {abs} (b)=d=\operatorname {sgn}(d)=\operatorname {abs} (d)=1$ immediately follows that $\mathbb {Z}$ with $\mathbb {Q}$ is compatible, so the same character can be used.

If two pairs are equivalent, then neither is

${\frac {a}{b}}<{\frac {c}{d}}$ nor c d <

The trichotomy of order states:

Exactly one of the following relationships applies:

· ${\frac {a}{b}}<{\frac {c}{d}}$

· ${\frac {a}{b}}\sim {\frac {c}{d}}$

Thus the rational numbers $(\mathbb {Q} ,<)$ totally ordered set.

→ The construction of the real numbers by means of Dedekind cuts is based on this order relation.

Properties

The rational numbers contain a subset that is isomorphic to the integers $\mathbb {Z}$ is isomorphic (choose for $z\in \mathbb {Z}$ the fraction representation ${\tfrac {z}{1}}$ ). This is often simplified by saying that the integers are contained in the rational numbers.

The body $\mathbb {Q}$ is the smallest body containing the natural numbers $\mathbb {N}$ . $\mathbb {Q}$ is namely the quotient body of the ring of integers $\mathbb {Z}$ , which is the smallest $\mathbb {N}$ containing ring. Thus $\mathbb {Q}$ is the smallest subbody of any upper body, so also of the body $\mathbb {R}$ of the real numbers - and thus its prime body. And as a prime body, $\mathbb {Q}$ rigid, that is, its only automorphism is the trivial one (the identity).

A real number is rational exactly if it is algebraic of the first degree. Thus the rational numbers themselves are a subset of the algebraic numbers $\mathbb A$ .

Between (in the sense of the order relation defined above) two rational numbers ${\tfrac {a}{b}}$ and ${\tfrac {c}{d}}$ is always another rational number, for example the arithmetic mean

${\frac {ad+bc}{2bd}}$

of these two numbers, and thus any number.

The rational numbers lie closely on the number line, that means: Each real number (illustratively: each point on the number line) can be approximated arbitrarily exactly by rational numbers.

Despite the tightness of $\mathbb {Q}$ in $\mathbb {R}$ there can be no function which is continuous only on the rational numbers (and on all irrational numbers is $\mathbb {R} \!\setminus \!\mathbb {Q}$ discontinuous) - vice versa is possible (for both statements see the article Thomae's function).

The set of rational numbers is equal to the set of natural numbers, i.e., it is countable. In other words, there is a bijective mapping between $\mathbb {Q}$ and $\mathbb {N}$ , which assigns to each rational number a natural number and vice versa. Cantor's first diagonal argument and the Stern-Brocot tree provide such bijective mappings. (The existence of equally powerful real subsets is equivalent to infinite power).

→ As a countable set, is a $\mathbb {Q}$ Lebesgue null set.

Division Algorithms

A rational number in the form of the ordered pair numerator/denominator represents an unexecuted division. The rational number is described thereby exactly and without loss of accuracy and in pure mathematics one is often satisfied with it. But already the comparison of two rational numbers is much easier, if the division is at least partially executed as division with remainder, which possibly leads to the mixed number.

A division is considered complete when the rational number in a place value system is developed to a certain base. A wide variety of algorithms have been designed for this purpose, which can be roughly divided into three groups:

Written division as an algorithm for manual calculation
Algorithms for use in computers

· Algorithms for integers of fixed (and small) length

· Algorithms for integers of arbitrary length

Examples of the latter are

the SRT division,
the Goldschmidt Division and
the Newton-Raphson division.

The latter two methods first form a kind of reciprocal of the denominator, which is then multiplied by the numerator. All methods are also suitable for short divisions and are also used there. The SRT division was initially implemented incorrectly in the division unit of Intel's Pentium processor, for example.

Decimal fraction expansion

Every rational number can be assigned a decimal fraction expansion. Rational numbers have a periodic decimal fraction expansion, while irrational numbers have a non-periodic one (which is also true for the -adic fraction expansions to other (different from bases (basic numbers) $g\in \mathbb {Z} \setminus \{-1,0,1\}$ holds). Here, a finite (i.e., terminating) decimal fraction expansion is only a special case of the periodic decimal fraction expansion, in that after the finite sequence of digits, the decimal digit 0 or $g-1$ repeats periodically. The period (the repeating part) is marked (in many countries, but not uniformly internationally) with an overline.

Examples are:

${\tfrac {1}{3}}$	$=0{,}{\overline {3}}$	$=0{,}33333\dotso$	$=\left[0{,}{\overline {01}}\right]_{2}$
${\tfrac {9}{7}}$	$=1{,}{\overline {285714}}$	$=1{,}285714\ 285714\dotso$	$=\left[1{,}{\overline {010}}\right]_{2}$
${\tfrac 15}$	$=0{,}2{\overline {0}}=0{,}1{\overline {9}}$	$=0{,}20000\dotso =0{,}19999\dotso$	$=\left[0{,}{\overline {0011}}\right]_{2}$
${\tfrac {1}{2}}$	$=0{,}5{\overline {0}}=0{,}4{\overline {9}}$	$=0{,}50000\dotso =0{,}49999\dotso$	$=\left[0{,}1{\overline {0}}\right]_{2}=\left[0{,}0{\overline {1}}\right]_{2}$
$1={\tfrac {1}{1}}$	$=1{,}{\overline {0}}=0{,}{\overline {9}}$	$=1{,}00000\dotso =0{,}99999\dotso$	$=\left[1{,}{\overline {0}}\right]_{2}=\left[0{,}{\overline {1}}\right]_{2}$

The square brackets indicate the corresponding evolutions in the binary system (base $g=2$ ).

The finite decimal or binary fraction expansions are exactly those which have at least two essentially different expansions (see also § Representation of rational numbers). They belong to the fractions whose truncated denominator merges into a power $g^{r}$ the base, so that the divisor $n|d$ which is alien to results in To distinguish from the cases below with $n>1$ (and non-terminating evolution), let the period length of such terminating evolution be $0$ assigned

According to Euler's theorem, for a denominator $n\in \mathbb {N} _{>1}$ a base g ∈ $g\in \mathbb {N}$

$g^{\varphi (n)}\equiv 1{\pmod {n}}$

with the Eulerian phi function φ $\varphi$ . The period length of 1/n is the order $l:=\operatorname {ord} _{n}(g)$ of the residue class $\left[g\right]$ in the unit group $(\mathbb{Z } /n\mathbb{Z } )^{\times }$ of the residue class ring $\Z/n\Z$ modulo . By Lagrange's theorem, is a divisor of the group order φ $\varphi(n)$ and therefore not larger than it. The Carmichael function λ $\lambda (n)$ is defined as the maximal element order in $(\mathbb{Z } /n\mathbb{Z } )^{\times }$ , is thus also a divisor of φ $\varphi(n)$ , and it holds for all $g,n$

$\operatorname {ord} _{n}(g)\;|\;\lambda (n)\;|\;\varphi (n)$ .

The number

$x:=(g^{l}-1)/n$

is integer, positive and $<g^{l}$ , and its digits evolved to base repeat continuously in the -adic representation of 1/n , thus:

$x\cdot \sum _{i=1}^{\infty }\left(g^{l}\right)^{-i}={\frac {x}{g^{l}-1}}={\frac {1}{n}}$

The above example 1/3 has $g=10$ the period length $\operatorname {ord} _{3}(10)=1$ base and the digit sequence $x={\overline {3}}$ and, for base g=2 the period length $\operatorname {ord} _{3}(2)=2$ and the digit sequence $x={\overline {01}}\;$ .

For given denominator n>1 the period l := occurs $l:=\operatorname {ord} _{n}(g)=\lambda (n)=\varphi (n)$ if the base g {\displaystyle g} is primitive root modulo n {\displaystyle Primitive roots exist if and only if the prime residue class group $(\mathbb{Z } /n\mathbb{Z } )^{\times }$ is cyclic, that is, if $n\in \{2,4,p^{r},2p^{r}\;\;|\;\;2<p\in \mathbb {P} ;\;r\in \mathbb {N} \}$ . Otherwise, λ $\lambda (n)$ and the period length a real divisor of φ $\varphi (n)\quad$ .

The table below gives the example of the bases $g=2,3,5$ and impression, for which denominators the period length (with matching numerator) is maximum (set in bold). For example, the decimal fraction expansions of the reciprocals of the primes $n=7,17,19,23,29$ have the period length λ $\lambda (n)=\varphi (n)=n-1=6,16,18,22,28$ . For composite numbers $n=12,15,21,33,35$ the maximum $\operatorname {ord} _{n}(g)\leq \varphi (n)/2$ ; for them, the values for φ $\varphi (n)$ and λ $\lambda (n)$ italicized. The worst case period length is given in ${\mathcal {O}}(n)$ , while the length $\scriptstyle \operatorname {len} _{g}(n)$ of the number in the -adic number system (also given in the table for comparison) is in $\mathcal{O}(\log n)$ The reciprocal 1/802787 of the prime 802787 requires at least 802786 bits in the dual system and at least 401393 digits in the decimal system-too many to display here.

$\textstyle n$	3	5	7	9	11	12	13	15	17	19	21	23	25	27	29	31	33	35	37	802787
$\textstyle \varphi (n)$	2	4	6	6	10	4	12	8	16	18	12	22	20	18	28	30	20	24	36	802786
$\textstyle \lambda (n)$	2	4	6	6	10	2	12	4	16	18	6	22	20	18	28	30	10	12	36	802786
$\textstyle \operatorname {ord} _{n}(2)$	2	4	3	6	10	- –	12	4	8	18	6	11	20	18	28	5	10	12	36	802786
$\scriptstyle \operatorname {len} _{2}(n)$	2	3	3	4	4	- –	4	4	5	5	5	5	5	5	5	5	6	6	6	20
$\textstyle \operatorname {ord} _{n}(3)$	- –	4	6	- –	5	- –	3	- –	16	18	- –	11	20	- –	28	30	- –	12	18	401393
$\scriptstyle \operatorname {len} _{3}(n)$	- –	2	2	- –	3	- –	3	- –	3	3	- –	3	3	- –	4	4	- –	4	4	13
$\textstyle \operatorname {ord} _{n}(5)$	2	- –	6	6	5	2	4	- –	16	9	6	22	- –	18	14	3	10	- –	36	802786
$\scriptstyle \operatorname {len} _{5}(n)$	1	- –	2	2	2	2	2	- –	2	2	2	2	- –	3	3	3	3	- –	3	9
$\textstyle \operatorname {ord} _{n}(10)$	1	- –	6	1	2	- –	6	- –	16	18	6	22	- –	3	28	15	2	- –	3	401393
$\scriptstyle \operatorname {len} _{10}(n)$	1	- –	1	1	2	- –	2	- –	2	2	2	2	- –	2	2	2	2	- –	2	6