Rational function

In mathematics, a rational function is a function that can be represented as the quotient of two polynomial functions. It therefore has the form

$f(x)={\frac {a_{m}x^{m}+a_{m-1}x^{m-1}+\dotsb +a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+\dotsb +b_{1}x+b_{0}}}={\frac {P_{m}(x)}{Q_{n}(x)}}$

with natural numbers and . The numbers $a_{m},\dotsc ,a_{0},b_{n},\dotsc ,b_{0}$ can be any real numbers (or complex numbers); the only restriction is that $Q_{n}\neq 0$ must be. The highest coefficients a_m and $b_{n}$ shall not be zero.

More abstractly, for the coefficients can $a_{m},\dotsc ,a_{0},b_{n},\dotsc ,b_{0}$ admit elements of any body. The rational functions with complex coefficients belong to the meromorphic functions.

More generally, one can consider rational functions in several variables as well as rational functions on algebraic varieties over arbitrary solids.

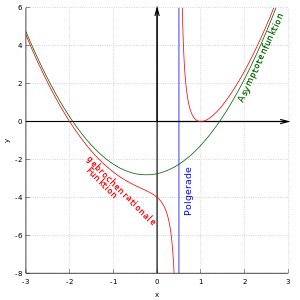
red: Graph of fractional function $f(x)={\tfrac {2(x+2)(x+1)(x-1)^{2}}{(x+1)(2x-1)}}$
blue: Pole line through the pole at x=0{,}5
green: asymptote function $g(x)=x^{2}+x/2-11/4$ , continuously rectifiable definition gap at x=-1

Division

If the denominator polynomial degree , i.e. constant, then one speaks of a completely rational function or of a polynomial function.
If the function term can be represented exclusively with a denominator polynomial of degree , then it is a fractional rational function.

If < n then it is a true fractional function.
If $m\geq n$ then it is a non-genuinely fractional function. It can be split into an integer function and a true fractional function via polynomial division (see below).

Examples of rational functions with different numerator degrees and denominator degrees :

Example	alternative spelling	m =	n =	Function type
$f\colon x\mapsto {\frac {3x^{3}-4x+5}{2}}$	$f\colon x\mapsto {\frac {3}{2}}x^{3}-2x+{\frac {5}{2}}$	3	0	fully rational
$f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}$		1	2	Genuinely broken-rational
$f\colon x\mapsto {\frac {(x-1)^{2}\cdot (x+2)}{x\cdot (2-3x^{2})}}$	$f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}$	3	3	fake broken rational
$f\colon x\mapsto x+1+{\frac {1}{x-1}}$	$f\colon x\mapsto {\frac {x^{2}}{x-1}}$	2	1	fake broken rational

Curve discussion

Using the function term of the rational function $f={p \over q}\colon x\mapsto {\frac {p(x)}{q(x)}}$ following statements can be made about the function graph (curve discussion).

Definition range, zeros and poles

The fractional function is not defined at the zeros of the denominator function

The zeros of a fractional rational function are determined by those zeros of the numerator function which belong to the definition range of the entire function.

A special case arises when a real number $a\in \mathbb{R}$ is simultaneously zero of the numerator polynomial and of the denominator polynomial. Then the numerator and denominator polynomials are divisible by the corresponding linear factor x-a (possibly even several times), i.e. the function term can be truncated with this factor (possibly several times).

If in the denominator occurs times more often than in the numerator (with natural number , is a pole (n {\displaystyle the multiplicity of the pole);
otherwise the rational function at the position has a definition gap that can be continuously eliminated, and one can continue the function continuously

Examples:

The function $f\colon x\mapsto {\frac {x-1}{(2x-4)^{2}}}$ has the domain of definition ${\mathbb {D}}={\mathbb {R}}\setminus \{2\}$ , since the denominator function $q\colon x\mapsto (2x-4)^{2}$ has the zero and the zero , since that is the only zero of the counter function $p\colon x\mapsto x-1$ (and belongs to $\mathbb {D}$ ). is a (double) pole.
The function $f\colon x\mapsto {\frac {x^{2}-x}{x^{2}-1}}$ has the domain of definition ${\mathbb {D}}_{f}={\mathbb {R}}\setminus \{\pm 1\}$ . But here is a zero of the numerator and the denominator function. To truncate the corresponding linear factor , first factorise the numerator and denominator (by factoring out or using the binomial formula). This leads to $f\colon x\mapsto {\frac {x\cdot (x-1)}{(x+1)\cdot (x-1)}}$ respectively. after shortening to $f\colon x\mapsto {\frac {x}{x+1}}$ . Thus it follows: is a (simple) pole, on the other hand is a continuously recoverable definition gap of and has the zero (note: is not a zero of since this value does not belong to $\mathbb {D}$ !). For the continuous continuation of get: ${\tilde {f}}(x)={\frac {x}{x+1}}$ and ${\mathbb {D}}_{{{\tilde {f}}}}={\mathbb {R}}\setminus \{-1\}$ .

Asymptotic behaviour

For the behaviour of towards infinity, the degrees or the numerator or denominator polynomial are decisive:

For $x\to\infty$ goes f(x)

(case 1) against $\operatorname {sgn} \left({\tfrac {a_{m}}{b_{n}}}\right)\cdot \infty$ , if where $\sgn$ represents the sign function.
(case 2) against ${\tfrac {a_{m}}{b_{n}}}$ if (the asymptote is parallel to the axis),
(case 3) towards $0$ (the axis is horizontal asymptote), if ,

For $x\to -\infty$ same limit value results in cases 2 and 3 as for $x\to \infty$ . In case 1, one has to consider the numerator and denominator degrees even more precisely:

If $m-n$ is even, the same limit value results as for $x\to \infty$ .
If is $m-n$ odd, the sign of the limit changes compared to $x\to \infty$

Examples:

For the fractional function $f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}$ the numerator degree and the denominator degree the limit value for $x \to \pm \infty$ is therefore $0$ .
The fractional rational function $f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}$ has the numerator degree and also the denominator degree ; since here $a_{3}=1$ and $b_{3}=-3$ , the equation of the horizontal asymptote gives: $y=-{\frac {1}{3}}$ .
The fractional rational function $f\colon x\mapsto {\frac {x^{2}}{x-1}}$ has the numerator degree and the denominator degree ; with the coefficients $a_{2}=1$ and $b_{1}=1$ thus obtain: $f(x)\to \operatorname{sgn} \left({\tfrac {1}{1}}\right)\cdot \infty =+\infty$ for $x\to \infty$ . Since here $m-n=1$ is odd, it follows for the limit for $x\to -\infty$ the reversed sign, i.e. $f(x)\to -\infty$ . This function can also be written as $f\colon x\mapsto x+1+{\frac {1}{x-1}}$ that is, the (oblique) asymptote has the equation (and this also easily results in the limit behaviour just described).

Investigation with polynomial division

In the above case 1 ( m>n decompose the function term by means of polynomial division into a sum of a polynomial and a true fractional term; the polynomial then describes a so-called asymptote curve. The behaviour of the function values for $x \to \pm \infty$ described above can also be obtained more simply by examining only the behaviour of this asymptote curve. In the special case m=n+1 an oblique asymptote results.

As above, stands for the degree of the numerator polynomial p(x) and degree of the denominator polynomial q(x) . Again, all cases are considered (not only

By means of polynomial division of p(x) by q(x) one first obtains a representation

$p(x)=g(x)\cdot q(x)+r(x)$

with polynomials g(x) and r(x) where the degree of r(x) is q(x) genuinely greater than that of From this follows the useful equation

$f(x)={p(x) \over q(x)}=g(x)+{r(x) \over q(x)}$ .

The asymptotic behaviour of f(x) is now the same as the asymptotic behaviour of the integral function ("asymptote function") g(x) . The quotient $r(x) \over q(x)$ plays no role.

If you have taken the trouble of polynomial division and set up the useful equation described above, you will find it easier to distinguish between cases. It applies:

Case 1: m < n → -axis is asymptote: g(x) = 0

Case 2: m=n → horizontal asymptote: $g(x)={\frac {a_{m}}{b_{n}}}$

Case 3: $m=n+1$ → oblique asymptote: $g(x)=bx+c$ with $b={\frac {a_{m}}{b_{n}}}$ and $c={\frac {a_{m-1}}{b_{n}}}-{\frac {a_{m}b_{n-1}}{b_{n}^{2}}}$

Case 4: $m>n+1$ → g(x) is a polynomial of degree m-n ; the leading coefficient of this polynomial is equal to ${\frac {a_{m}}{b_{n}}}$ .

Symmetry

A polynomial function (integer function) is even/odd if all exponents are even/odd. If numerator polynomial and denominator polynomial of one of these two types, the rational function is also even or odd:

If and are both even or both odd, then is even (i.e. the graph is symmetrical to the y-axis).
If is even and is odd, then is odd (i.e. the graph is point-symmetric with respect to the origin); the same applies if odd and even.

In all other cases, i.e. when numerator or denominator function or both are neither even nor odd, symmetry properties of are more difficult to decide. (See also discussion of curves and symmetry in geometry).

Examples:

The graph of the function with $f(x)={\frac {2x^{3}-3x}{x^{2}+1}}$ is symmetric about the origin, since odd and even, so the function as a whole is odd.
The graph of the function $f\colon x\mapsto {\frac {x^{5}-x^{3}}{x^{3}+x}}$ is symmetrical to the y-axis, because and both odd, so the function as a whole is even. This can also be seen differently: If you exclude x from the numerator and denominator, you can shorten the function term to $f(x)={\frac {x^{4}-x^{2}}{x^{2}+1}}$ ; now and are even, so the function as a whole is even again.
The graph of the function with the term $f(x)={\frac {x}{x-1}}$ not show any symmetry at first ( is odd, but is neither even nor odd); however, it can be shown that the graph is symmetrical to the point P(1|1); namely, it holds:

$f(1+x)-1={\frac {1+x}{(1+x)-1}}-1={\frac {1+x}{x}}-{\frac {x}{x}}={\frac {1}{x}}$ and

$1-f(1-x)=1-{\frac {1-x}{(1-x)-1}}={\frac {x}{x}}+{\frac {1-x}{x}}={\frac {1}{x}}$ ,

so in total: f(1+x)-1=1-f(1-x) which means straight symmetry to the point P(1|1). Alternatively, one can also show that the graph of consists of the graph of the function $g\colon x\mapsto {\frac {1}{x}}$ (which is symmetrical to the origin) by shifting it by 1 in the direction and by 1 in the direction.

Derivation

To derive fractional rational functions, one must generally use the quotient rule; in addition, the chain rule can often be useful, for example, if the denominator function is a power of a binomial. Before deriving, it is often advisable to first rewrite the function term with the help of a polynomial division and to shorten the remaining true fractional term.

Examples:

For the function $f\colon x\mapsto {\frac {2x-1}{(x^{2}+1)^{2}}}$ it makes sense to apply the chain rule in addition to the quotient rule instead of first applying the first binomial formula in the denominator. With the chain rule, the derivative of the denominator function (in the quotient rule usually denoted by ):

$q'(x)=2(x^{2}+1)\cdot 2x=4x(x^{2}+1)$ ,

and thus altogether for the derivative function of :

$f'(x)={\frac {2\cdot (x^{2}+1)^{2}-(2x-1)\cdot 4x(x^{2}+1)}{(x^{2}+1)^{4}}}$ .

Now you can factor out $(x^{2}+1)$ in the numerator and shorten it:

$f'(x)={\frac {2\cdot (x^{2}+1)-(2x-1)\cdot 4x}{(x^{2}+1)^{3}}}$ .

Simplifying the counter finally leads to

$f'(x)={\frac {-6x^{2}+4x+2}{(x^{2}+1)^{3}}}$ .

The function term $f(x)={\frac {x^{4}+x^{3}-7x^{2}-12x-4}{3x^{3}+12x^{2}+12x}}$ is first brought to the form with the help of a polynomial division.

$f(x)={\frac {1}{3}}x-1+{\frac {x^{2}-4}{3x^{3}+12x^{2}+12x}}$ ,

from which you can also read off the equation of the oblique asymptote:

$y={\frac {1}{3}}x-1$ .

Factorising numerator and denominator then leads to

$f(x)={\frac {1}{3}}x-1+{\frac {(x+2)(x-2)}{3x(x+2)^{2}}}$ ,

one can therefore (x+2) truncate a factor Finally one has:

$f(x)={\frac {1}{3}}x-1+{\frac {x-2}{3x^{2}+6x}}$ ;

in this form it is now much easier to derive the function than in the one originally given.

With the help of the quotient rule we get:

$f'(x)={\frac {1}{3}}+{\frac {1\cdot (3x^{2}+6x)-(x-2)\cdot (6x+6)}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-3x^{2}+12x+12}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}$ .

If one sets the first derivative equal to zero in order to search for the extreme points, it is advisable to combine the two fractions again beforehand:

$f'(x)={\frac {x^{2}(x+2)^{2}-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}={\frac {x^{4}+4x^{3}+3x^{2}+4x+4}{3x^{2}(x+2)^{2}}}$ .

Stem function

In contrast to the integral functions, it is often relatively difficult to find a root function for fractional functions. Depending on the form of the fractional function, the following rules can be applied (usually the function term must first be brought into a suitable form by transformations and/or substitutions):

$\int {\frac {1}{mx+a}}dx={\frac {1}{m}}\cdot \ln(mx+a)+C$ for $m,a\in {\mathbb {R}},m\neq 0$

$\int {\frac {1}{(mx+a)^{n}}}dx={\frac {1}{m}}\cdot {\frac {-1}{n-1}}\cdot {\frac {1}{(mx+a)^{{n-1}}}}+C$ for $m,a\in {\mathbb {R}},m\neq 0,n\in {\mathbb {N}}\setminus \{0;1\}$

$\int {\frac {1}{x^{2}+1}}dx=\arctan(x)+C$ or $=-\operatorname {arccot}(x)+C$

$\int {\frac {1}{x^{2}-1}}dx=\operatorname {artanh}(x)+C={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)$ for |x| < 1

$\int {\frac {1}{x^{2}-1}}dx=\operatorname {arcoth}(x)+C={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)$ for |x| > 1

$\int {\frac {u'(x)}{u(x)}}dx=\ln |u(x)|+C$ for $u(x)\neq 0$

Often the partial fraction decomposition can also be helpful for determining a parent function. Examples:

Let us look for a primitive function of $f(x)={\frac {5x-1}{3x+2}}$ . By means of a polynomial division, this can first be rewritten as:

$f(x)={\frac {5}{3}}-{\frac {13}{9x+6}}$ .

Applying the first rule then yields as possible root function:

$F(x)={\frac {5}{3}}x-{\frac {13}{9}}\ln(9x+6)$ .

Let us find a primitive function for $f(x)={\frac {x^{2}+1}{x^{2}-1}}$ where should lie between -0.5 and 0.5. Again, the function term can first be rewritten using polynomial division:

$f(x)=1+{\frac {2}{x^{2}-1}}$ .

Applying the fourth rule then yields as possible root function:

$F(x)=x+2\cdot \operatorname {artanh}(x)$ .

Let us find a root function of $f(x)={\frac {x+2}{x^{2}+4x+5}}$ . This can also be written as

$f(x)={\frac {1}{2}}{\frac {2x+4}{x^{2}+4x+5}}={\frac {1}{2}}{\frac {u'(x)}{u(x)}}$ with $u(x)=x^{2}+4x+5$ .

Applying the last rule then yields as possible root function:

$F(x)={\frac {1}{2}}\ln(x^{2}+4x+5)$ .

A primitive function to $f(x)={\frac {1}{x^{2}+2x+2}}$ can be determined using the substitution after transforming the denominator using quadratic completion:

${\begin{aligned}\int {\frac {1}{x^{2}+2x+2}}dx&=\int {\frac {1}{(x+1)^{2}+1}}dx=\int {\frac {1}{y^{2}+1}}dy\\&=\arctan(y)+C=\arctan(x+1)+C\end{aligned}}$

A primitive function to $f(x)={\frac {1}{x^{2}-x-6}}$ can be obtained by partial fraction decomposition after first factorising the denominator:

${\begin{aligned}\int {\frac {1}{x^{2}-x-6}}dx&=\int {\frac {1}{(x-3)(x+2)}}dx=\int {\frac {1}{5}}\left({\frac {1}{x-3}}-{\frac {1}{x+2}}\right)dx\\&={\frac {1}{5}}\left(\ln(x-3)-\ln(x+2)\right)+C={\frac {1}{5}}\ln \left({\frac {x-3}{x+2}}\right)+C\end{aligned}}$

Rational functions in several variables

A rational function in variables $x_{1},\ldots ,x_{n}$ is a function of the form $f(x_{1},\ldots ,x_{n})={\frac {P(x_{1},\ldots ,x_{n})}{Q(x_{1},\ldots ,x_{n})}}$ where and $x_{1},\ldots ,x_{n}$ are polynomials in the indefinites and $Q\not =0$ .

Examples

$f(x_{1},\ldots ,x_{n})={\frac {x_{1}^{2}+\ldots +x_{n}^{2}}{1-x_{1}\ldots x_{n}}}$
$f(x,y)={\frac {xy}{x+y}}$
$f(m,M)={\frac {m}{2M+m}}g$

Continuity

The domain of consists of those points $(x_{1},\ldots ,x_{n})$ which are either not a zero of or whose multiplicity as a zero of at least as large as the multiplicity as a zero of . Rational functions are continuous in all points of their domain.

Applications

Rational functions have many applications in science and technology:

Many quantities are inversely proportional to each other, so one of the quantities is a rational function of the other, with the numerator constant and the denominator a (homogeneous) linearfunction. A few examples:

velocity and the time required for a fixed distance are inversely proportional to each other: $t(v)={\tfrac {s}{v}}$
The concentration a substance is inversely proportional to the volume the solvent for a fixed amount of substance : $C(V)={\tfrac {n}{V}}$
Acceleration and mass are inversely proportional to each other for a fixed force : $a(m)={\tfrac {F}{m}}$ .
For the capacitance a plate capacitor, the following applies as a function of the plate spacing : $C(d)=\epsilon _{0}\epsilon _{r}{\tfrac {A}{d}}$ with the area the plates, the electric field constant $\epsilon _{0}$ and the permittivity $\epsilon_r$ .

In many areas of physics, functions of two variables and the following form occur: $f(x;y)={\tfrac {xy}{x\pm y}}$ . If one of the two variables, e.g. is constant or chosen as a parameter, the result is a rational function (or set of functions) of . Such functions always occur when the total reciprocal of some quantity results as the sum or difference of the reciprocals of two other functions.

Using the lens equation of optics, one can represent the focal length as a function of object width and image width : $f(g;b)={\tfrac {gb}{g+b}}$ ; rearranging to or yield a very similar function, but with - instead of +.
For the total resistance a parallel connection of two resistors $R_{1}$ and $R_{2}$ get: $R={\tfrac {R_{1}R_{2}}{R_{1}+R_{2}}}$ ; an analogous formula applies to the series connection of two capacitors.
In mechanics, if two springs with spring constants $D_{1}$ and $D_{2}$ attached to each other, the following results for the total spring constant of the arrangement: $D={\tfrac {D_{1}D_{2}}{D_{1}+D_{2}}}$

For a voltage divider, the total voltage dropping across a resistor given by: $U(R)={\tfrac {U_{0}R}{R+R'}}$ where $U_{0}$ the voltage to be divided and the other resistance.
For the electrical power produced by a device with resistance connected to a voltage source (voltage ) with internal resistance $R_{i}$ : $P(R)={\tfrac {U^{2}R}{(R+R_{i})^{2}}}$ . The greatest possible power (to be determined with the aid of differential calculus) is therefore obtained when $R=R_{i}$ (power matching).
For the inductance of a (not too short) coil as a function of its radius applies: $L(r)={\tfrac {\mu _{0}N^{2}\pi r^{2}}{l+r/1,1}}$ . Where the length of the coil (so can also be taken as a rational function of ), is the number of turns and μ $\mu _{0}$ is the magnetic field constant.
The braking force an eddy current brake depends on the velocity as follows: $B(v)={\tfrac {av}{b+v^{2}}}$ with constants and .
In Atwood's machine, the acceleration depends on the two masses and as follows: $a={\tfrac {m}{2M+m}}\cdot g$ ; thus one can take as a rational function of both and
Geometric questions also often lead to rational functions. Example: For a chest consisting of a cuboid (basic side lengths and , height ) with an attached half-cylinder (height , radius ), the following applies to the surface area function of given volume : $O(r)={\tfrac {(\pi +4)r^{3}+2V}{r}}$ .

Deviant meaning in abstract algebra

Rational functions over any body

→ Main article: Rational function body

In abstract algebra, the term rational function is used in a more general and somewhat different sense. Namely, one understands by a rational function in variables $X_1, X_2, \dotsc, X_n$ over a body an element of the quotient body of the polynomial ring $K\left[X_{1},X_{2},\dotsc ,X_{n}\right]$ . This quotient body is called a rational function body.

In general, then, a rational function is not a function of any kind, but a (formal) fraction of two polynomials. The inverse need not hold, but the difference is only noticeable over finitebodies: For example, for any prime over the finite body $\mathbb {F} _{p}$ (the body of all residue classes of integers modulo ) the fraction ${\tfrac {1}{X^{p}-X}}$ a well-defined rational function in the variable but not a function in the true sense of the term, because you cannot put a single value into this function without the denominator becoming 0. (For if one puts any $x\in {\mathbb F}_{p}$ into this "function", you get ${\tfrac {1}{x^{p}-x}}$ which is undefined because the denominator 0 according to $x^{p}-x$ Fermat's little theorem). Over infinite bodies, however, a rational function is always a function that may have a gap in definition, but this gap in definition is only very small compared to the domain of definition. This idea is formalised by the notion of Zariski topology: The definition gap is a Zariski-closed set, and the closed hull of the definition domain is the whole set.

Rational functions on an algebraic variety

→ Main article: Rational function body#Function bodies in algebraic geometry

Let be an algebraic variety defined by polynomials $f_{1},\dotsc ,f_{m}\in k\left[x_{1},\dotsc ,x_{n}\right]$ , so

$V=\{x\in {\mathbb A}^{n}\mid f(x)=0{\text{ für alle }}f\in S\}.$

$I(V)=\{f\in k[x_{1},\dotsc ,x_{n}]\mid f(x)=0{\text{ für alle }}x\in V\}.$

The ring of entire functions is $k[x_{1},\dotsc ,x_{n}]/I(V)$ . The body of rational functions is the quotient body of the ring of integer functions.

More generally, there is the notion of rational mappings between (quasi-projective) varieties. Rational functions are the special case of rational mappings from a variety to $\mathbb {A} ^{1}$ .

Rational function

Division

Curve discussion

Definition range, zeros and poles

Asymptotic behaviour

Symmetry

Derivation

Stem function

Rational functions in several variables

Examples

Continuity

Applications

Deviant meaning in abstract algebra

Rational functions over any body

Rational functions on an algebraic variety

Search by letter