Rate equation

This article or section needs revision. More details should be given on the discussion page. Please help improve it and then remove this marker.

Rate equations are equations that describe the time course of concentration of different chemical substances in coupled chemical reactions, or the occupation course of the energy levels in atoms or molecules in excitation and de-excitation processes.

Rate equations describe the reaction kinetics.

The rate of change of the concentration $c_{i}$ a species is the sum of the rates of change of the concentrations caused by different reactions:

${\frac {\mathrm {d} c_{i}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}{\frac {\mathrm {d} c_{i,r}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}\nu _{i,j}r_{j},$ ,

where is the species under consideration, $c_{i}$ its concentration and an index which runs over all reactions occurring (i.e. also over the outward and reverse reaction in each case). $r_{j}$ is the reaction rate of reaction . The reaction rate $r_{j}$ is proportional to the product of the reactant activities $a_{j,l}^{|\nu _{j,l}|}$ of reaction with the rate constant k_j the reaction as proportionality constant:

$r_{j}=k_{j}\prod _{l}a_{j,l}^{|\nu _{j,l}|}$ .

This gives the rate equation as:

${\frac {\mathrm {d} c_{i}}{\mathrm {d} t}}=\sum _{j=1}^{N_{\mathrm {R} }}\nu _{ij}k_{j}\prod _{k=1}^{N_{j}}a_{k}^{b_{kj}},$

where

$a_{i}$ is the activity of species $i\,$ - often the concentration $c_{i}$ used for simplification -,
$\nu_{ij}$ the stoichiometric coefficients of species in reaction ,
$b_{{ij}}$ the amounts of the stoichiometric coefficients, if the rate equation is set up with activities, or the partial reaction orders of species in reaction (generally unequal to the stoichiometric coefficients), if the rate equation is set up with concentrations,
the rate coefficients (generally rate constants),
$N_{\mathrm {R} }$ is the number of reactions and
is the number of substances involved in the reaction

The rate equations are generally a system of coupled, stiff, first-order nonlinear differential equations for which building block conservation must hold. In the stationary case $(\mathrm {d} c_{i}/\mathrm {d} t=0)$ the law of mass action results. Rate equations can be represented compactly using the stoichiometric matrix.

By solving the differential equations, the time course of the mean concentrations is obtained. To obtain realisations of the concentrations including fluctuations, stochastic simulations can be carried out with the Gillespie algorithm.

Derivation

The rate equations can be derived for all species involved by setting up the continuity equation with source and sink terms (or a balance equation) for the particle concentrations:

${\frac {\partial c_{i}}{\partial t}}+\operatorname {div} {\vec {j}}_{i}=f_{i}(\{a_{i}\})$ ,

where $f_{i}(\{a_{i}\})$ is the source term which $a_{i}(\{c_{i}\})$ depends on the activities These activities are in general again non-trivially dependent on all concentrations.

Since an equilibrium reaction always has an outward reaction and a reverse reaction, the outward reaction rate $k_{\text{+,r}}$ and the reverse reaction rate $k_{\text{-,r}}$ exist. The source term is given by a sum over all reactions:

$f_{i}(\{a_{i}\})=\sum _{r}|\nu _{i,r}|\left[-k_{\text{-,r}}\prod _{{\text{Reaktanden j}},r}a_{r,j}^{|\nu _{r,j}|}+k_{\text{+,r}}\prod _{{\text{Produkte j}},r}a_{r,j}^{|\nu _{r,j}|}\right].$

Note that the partial reaction order (the exponent with which the concentrations enter) only corresponds to the amount of the stoichiometric coefficients if activities are used. If concentrations are also used in the source term instead of activities and particle interactions are present, the amounts of the stoichiometric coefficients are to be replaced with the partial reaction orders. The partial reaction order can assume any values (e.g. 0) and is determined experimentally.

Various cases

At equilibrium, there are no particle flows ( ${\vec {j}}_{i}={\vec {0}}\,\forall i$ ) and the particle concentrations no longer change in time. Therefore, at equilibrium:

$0=f_{i}(\{a_{i}\}).$

Assuming that each reaction (as a pair of outward and backward reactions) is balanced in detail, the law of mass action is obtained for each reaction by transformation:

$K_{r}={\frac {k_{\text{-,r}}}{k_{\text{+,r}}}}={\frac {\prod _{{\text{Produkte j}},r}a_{r,j}^{|\nu _{r,j}|}}{\prod _{{\text{Reaktanden j}},r}a_{r,j}^{|\nu _{r,j}|}}}$

If the system is in non-equilibrium but homogeneous, no particle currents occur, but the concentrations change in time until equilibrium is reached:

${\frac {\partial c_{i}}{\partial t}}=f_{i}(\{a_{i}\})$

In the case where one considers an inhomogeneous system in non-equilibrium, the particle flow ${\vec {j}}_{i}\neq 0$ and can be given by Fick's first law

${\vec {j}}_{i}=-{\vec {\nabla }}(D_{i}c_{i}({\vec {r}}))+{\vec {j}}_{i}^{\text{excess}}$

(whereby the non-ideal excess term only occurs for non-ideal systems). One then obtains a reaction diffusion equation.

In the case that there is additional flow in the system, convection in the particle flow must be taken into account and the convection-diffusion equation is obtained.

Examples

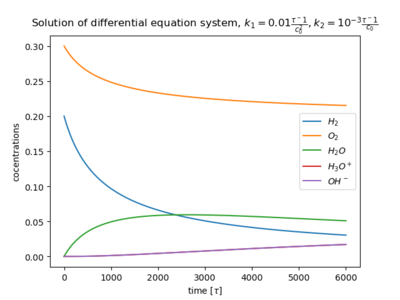
Hydrogen oxidation

Hydrogen oxidation is used to illustrate this:

$\displaystyle \mathrm {2H_{2}+O_{2}\longrightarrow 2H_{2}O}$

(Rate coefficient: $\displaystyle k_{1}$ )

a part dissociates

$\displaystyle \mathrm {2H_{2}O\longrightarrow H_{3}O^{+}+OH^{-}}$

(Rate coefficient: $\displaystyle k_{2}$ )

The rate equations (Eq.1) for the five species are:

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}]} =-2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[O_{2}]} =-k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}O]} =+2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]} -2k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{3}O^{+}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[OH^{-}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

The concentrations of the species:

$c_{1}\equiv \mathrm {[H_{2}]} ,\;\;c_{2}\equiv \mathrm {[O_{2}]} ,\;\;c_{3}\equiv \mathrm {[H_{2}O]} ,\;\;c_{4}\equiv \mathrm {[H_{3}O^{+}]} ,\;\;c_{5}\equiv \mathrm {[OH^{-}]}$

Belousov-Zhabotinsky reaction

→ Main article: Belousov-Zhabotinsky reaction

Oscillating reactions are described by rate equations. For special models on this, see Oregonator and Brusselsator. The numerical solution of such systems of differential equations then yields oscillating chemical concentrations.

Lotka-Volterra equations

→ Main article: Lotka-Volterra equations

The interaction of predator and prey populations is described by the Lotka-Volterra equations.

Numerical solution, using scipy.integrate.odeint. The reaction rates $k_{1},k_{2}$ and the initial concentrations are arbitrarily chosen in this example. $c_{0}$ is a reference concentration.

Numerical solution methods

Since the rate equations are a system of stiff differential equations, one is forced to choose a method with as large a stability region as possible so that the integration steps do not become too small. A-stable methods are the most favourable.

For the rate equations, 'stiff' means that the time constants of the different species differ very much: Relative to others, some concentrations change very slowly. Two examples of absolutely stiff-stable integration methods are the Implicit Trapezoidal Method and the Implicit Euler Method, as well as some BDF (backward differentiation formula) methods.

Building block conservation

The principle of building block conservation provides a way to check the goodness of the numerical solutions, because it applies at all times:

$\sum _{i=1}^{N_{\mathrm {Sp} }}c_{i}\beta _{ik}=\gamma _{k}={\text{const.}},\quad \forall k=1,\dots ,N_{\mathrm {B} }$

where

$N_{{\mathrm {B}}}\,$ Minimum number of building blocks,

$N_{{\mathrm {Sp}}}\,$ Number of species involved in the reactions.

Derivation

A species i, here written as $A_{i}$ the building blocks $B_{k}$ as follows:

$A_{i}=\sum _{{k=1}}^{{N_{{\mathrm {B}}}}}\beta _{{ik}}B_{k}\quad \Rightarrow \quad \sum _{{i=1}}^{{N_{{\mathrm {Sp}}}}}\nu _{{ij}}\beta _{{ik}}=\underline {\underline {0}}$ .

into the rate equation (Eq.1) and summed over all species, yields the above building block conservation because of $\sum _{{i=1}}^{{N_{{\mathrm {Sp}}}}}{\dot c}_{i}\beta _{{ik}}=0$ .

Example for the matrix βik

${\begin{pmatrix}\mathrm {H_{2}} \\\mathrm {O_{2}} \\\mathrm {H_{2}O} \\\mathrm {H_{3}O^{+}} \\\mathrm {OH^{-}} \end{pmatrix}}=\underbrace {\begin{pmatrix}2&0&0\\0&2&2\\2&1&1\\3&1&0\\1&1&2\end{pmatrix}} _{\beta _{ik}}\cdot {\begin{pmatrix}\mathrm {H} \\\mathrm {O^{+}} \\e^{-}\end{pmatrix}}$

Questions and Answers

Q: What is the rate equation?

A: The rate equation (or rate law) is an equation used to calculate the speed of a chemical reaction. It takes into account the concentrations of reactants and products, as well as other conditions such as temperature and pressure.

Q: How can the rate constant be calculated?

A: In special cases, it is possible to solve the differential equation and find k by integrating it. For example, in a first-order reaction, a plot of ln[A] against time t will give a straight line with a slope of -k.

Q: What does x and y represent in the general reaction formula?

A: x and y depend on which step is rate-determining. If the reaction mechanism is very simple, where A and B hit each other then go to products through one transition state, then x=a and y=b.

Q: Is there another way to calculate k if one reagent has a high concentration?

A: Yes, if one reagent has a high concentration that can be thought of as constant then it becomes what's known as pseudo-first order rate constant (k'). This can also be used to calculate k'.

Q: How does temperature affect the rate constant?

A: The rate constant changes with temperature, pressure and other conditions.

Q: What type of equation is the rate equation?

A: The rate equation is a differential equation.

Rate equation

Derivation

Various cases

Examples

Hydrogen oxidation

Belousov-Zhabotinsky reaction

Lotka-Volterra equations

Numerical solution methods

Building block conservation

Derivation

Example for the matrix βik

See also

Questions and Answers

Q: What is the rate equation?

Q: How can the rate constant be calculated?

Q: What does x and y represent in the general reaction formula?

Q: Is there another way to calculate k if one reagent has a high concentration?

Q: How does temperature affect the rate constant?

Q: What type of equation is the rate equation?

Search by letter