Radian
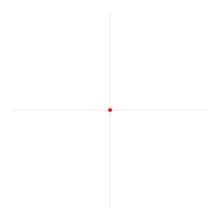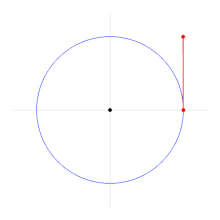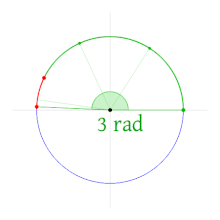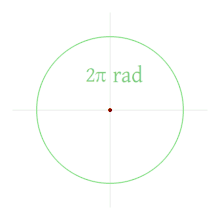
The radian (unit symbol: rad) is an angle measure in which the angle is given by the length of the corresponding arc in the unit circle. Because of the consideration of the arc of a circle to indicate the angle, the indication "in radians" is also called the angle of arc. The arc length of a given angle is proportional to the radius 


In many calculations in physics and mathematics, radians are the most useful angular measure, see for example angular velocity and sine and cosine.
In the International System of Units (SI), radian is the special name for the coherent, derived SI unit m/m with the dimension number. It is therefore an auxiliary unit of measurement and can simply be replaced by 1 in calculations, i.e. 1 rad = 1. The unit can be combined with SI prefixes, e.g. mrad for milliradian.
In practice, the unit abbreviation rad is often omitted when the angle measure 
The angle marking the length of the radius on the circumference of the circle is 1 rad, so the solid angle is 
Conversion between radian and degree
| Frequently used values: | |
| Grade | Radiant |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Scientific calculators calculate angle functions either in degrees or in radians, sometimes also in gons, where the full angle is 400 gons. The calculation modes on most pocket calculators are called "DEG" (from English degree for degree) for the degree measure, "RAD" for the radian and "GRD", "GRA" or "GRAD" for the gon angle measure, and are sometimes cyclically switchable via a combination key "DRG" (from the initial letters of the units).
Angle functions in mathematical libraries for programming languages and in spreadsheet programs usually use radians, so degrees usually need to be converted. The solid angle has 2 π 
or:
So the factor for converting radians to degrees is
Examples:
Historical
The SI initially left open whether radians and steradians were derived units or base units; the class of "supplementary units" was created for both. In 1980, the CIPM recommended that these supplementary units be interpreted as derived. This was followed in 1995 by the 20th CGPM, which decided to abolish the class of supplementary units.
Search within the encyclopedia