Quicksort
Quicksort (quick 'fast' and to sort 'sort') is a fast, recursive, non-stable sorting algorithm that works according to the divide and conquer principle. It was developed in its basic form by C. Antony R. Hoare in about 1960 and has since been improved by many researchers. The algorithm has the advantage that it has a very short inner loop (which greatly increases execution speed) and that, apart from the extra space needed on the call stack for recursion, it does not require any extra memory.
On average, the quicksort algorithm performs 

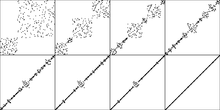
The numbers from 1 to n in random order are sorted with Quicksort.
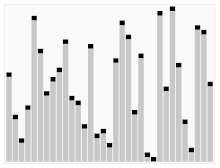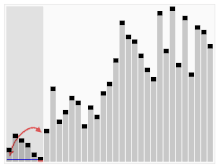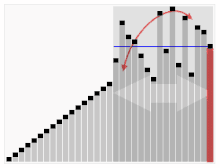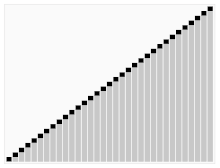
A random permutation of integer values is sorted with Quicksort. The blue lines show the value of the red marked pivot element in the respective recursion step.
Principle
First, the list to be sorted is separated into two sub-lists ("left" and "right" sub-lists). To do this, Quicksort selects a so-called pivot element from the list. All elements smaller than the pivot element go into the left sublist, and all elements larger than the pivot element go into the right sublist. The elements that are equal to the pivot element can be distributed among the sublists as desired. After the distribution, the elements of the left list are smaller than or equal to the elements of the right list.
Afterwards, each sublist must be sorted in itself to complete the sorting. To do this, the quicksort algorithm is executed on the left and right sublists. Each sublist is then split into two sublists and the quicksort algorithm is applied to each of them again, and so on. These self-calls are called recursion. If a sublist of length one or zero occurs, it is already sorted and the recursion is aborted.
The positions of the elements that are equal to the pivot element depend on the division algorithm used. They can be distributed arbitrarily among the sublists. Since the order of equal elements to each other can change, Quicksort is generally not stable.
The procedure must ensure that each of the sublists is at least one shorter than the total list. Then the recursion is guaranteed to end after a finite number of steps. This can be achieved, for example, by setting the element originally selected as a pivot to a place between the sublists and thus not belonging to any sublist.
Pseudocode
The implementation of the division is done as an in-place algorithm: The elements are not copied into additional memory, but only swapped within the list. For this, a procedure called splitting or also partitioning is used. After that, the two sub-lists are equally in the right position. As soon as the partial lists have been sorted into themselves, the sorting of the complete list is finished.
The following pseudocode illustrates how the algorithm works, where data is the list of n elements to be sorted. On each call to quicksort(), the index of the first element in the sublist is given on the left and the index of the last element on the right. In the first call (top recursion level), left = 0 and right = n-1. The passed list is divided recursively until it contains only one value.
The following implementation of the divide function divides the field so that the pivot element is in its final position and all smaller elements come before it, while all larger elements come after it:
function divide(left, right) i := left // Start with j to the left of the pivot element j := right - 1 pivot := data[right] repeat as long as i < j // as long as i has not passed j // Search from the left for an element that is greater than or equal to the pivot element repeat as long as i < right and data[i] < pivot i := i + 1 end // search from the right an element that is smaller than the pivot element repeat as long as j > left and data[j] >= pivot j := j - 1 end if i < j then swap data[i] with data[j] end end // swap pivot element (data[right]) with new final position (data[i]) // and return the new position of the pivot element, end pass if data[i] > pivot then swap data[i] with data[right] end answer i endAfter selecting the pivot element, an element is first searched for starting from the beginning of the list (index i), which is larger than the pivot element. Accordingly, starting from the end of the list, an element smaller than the pivot element is searched for (index j). The two elements are then swapped and end up in the correct sublist. The two searches are then continued from the positions reached until the lower and upper searches meet; this is the boundary between the two sublists.
Questions and Answers
Q: What is Quicksort?
A: Quicksort is a sorting algorithm used to sort items in an array.
Q: Who created Quicksort?
A: Tony Hoare created Quicksort in 1959.
Q: Is Quicksort still widely used today?
A: Yes, Quicksort is still widely used today.
Q: How does Quicksort sort an array?
A: Quicksort splits the array into two parts and continues to split those parts into more parts, sorting along the way by using a comparison sort.
Q: What is a comparison sort?
A: A comparison sort is a sorting algorithm that chooses a pivot point in a part of the array and then compares it with all the other points in that part of the array.
Q: Is Quicksort a stable sorting algorithm?
A: No, Quicksort is not a stable sorting algorithm.
Q: What is the time complexity of Quicksort?
A: The time complexity of Quicksort is O(n log n) on average, but O(n^2) in the worst case scenario.
Search within the encyclopedia