Quadratic equation

A quadratic equation is an equation that can be expressed in the form

$ax^{2}+bx+c=0\quad$

with $a\neq 0$ . Here are a,b,c coefficients; is the unknown. If additionally , it b=0 is called a pure quadratic equation.

Their solutions can be calculated using the formula

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

determine. In the domain of real numbers the quadratic equation can have no, one or two solutions. If the expression under the root is negative, no solution exists; if it is zero, one solution exists; if it is positive, two solutions exist.

The left-hand side of this equation is the term of a quadratic function (more generally, a second-degree polynomial), $f(x)=ax^{2}+bx+c$ ; the function graph of this function in the Cartesian coordinate system is a parabola. Geometrically, the quadratic equation f(x)=0 describes the zeros of this parabola.

General form - Normal form - Zero form

The general form of the quadratic equation is

$ax^{2}+bx+c=0\qquad (a\neq 0)\ .$

Here $ax^{2}$ is called quadratic term, linear term and constant term (or absolute term) of the equation.

The equation is in normal form if a=1 , so if the quadratic member has coefficient 1. From the general form, the normal form can be obtained by equivalence transformations by $a\neq 0$ dividing by With the definition

and $p={\frac {b}{a}}$ $\displaystyle q={\frac {c}{a}}$

the normal form can thus be written as

$x^{2}+px+q=0\ .$

If one side of an equation is 0, it is also called zero form.

In the following, quadratic equations with real numbers as coefficients , and respectively as and .

Solutions of the quadratic equation with real coefficients

A solution of the quadratic equation is a number that satisfies the equation when substituted for Every quadratic equation, if complex numbers are allowed as solutions, has exactly two (possibly coincident) solutions, also called roots of the equation. Considering only the real numbers, a quadratic equation has zero to two solutions.

Number of real zeros

The number of solutions can be determined with the help of the so-called discriminant (from Latin "discriminare" = "to distinguish"). In the general case $D=b^{2}-4ac$ , in the normalized case $D=p^{2}-4q$ (for derivation see below):

The graph shows the relationship between the number of real zeros and the discriminant:

A Discriminant positive: The parabola has two intersections with the axis, so there are two distinct real zeros $x_{1}$ and $x_{2}\ .$
B discriminant zero: The parabola has exactly one point of contact with the axis, namely its vertex. Thus, there is exactly one (double) real solution. The quadratic equation $ax^{2}+bx+c=0$ reduced to the form $a\cdot (x-x_{1})^{2}=0$
C Discriminant negative: The parabola has no intersection with the axis, there are no real solutions of the quadratic equation. If we allow complex numbers as the basic set for the solutions, we get two different complex solutions. These are conjugate to each other, that is, they have the same real part and their imaginary parts differ only by the sign.

Simple special cases

If the coefficient of the linear element b=0 or the absolute element c=0 then the quadratic equation can be solved by simple equivalent transformations without the need for a general solution formula.

Missing linear element

The purely quadratic equation $ax^{2}+c=0$ with $a\neq 0$ is equivalent to

$x^{2}=-{\frac {c}{a}}\ .$

The solutions are

$x_{1,2}=\pm {\sqrt {-{\frac {c}{a}}}}\ .$

In the case $a\,c<0\,$ two solutions exist. In the case $a\,c>0\,$ ${\tfrac {c}{a}}>0$ solutions exist for c a > The complex solutions are then

$x_{1,2}=\pm \mathrm {i} {\sqrt {\frac {c}{a}}}\ .$

For example, the equation $x^{2}-3=0$ has the solutions $x_{1,2}=\pm {\sqrt {3}}$ . The equation $2x^{2}+8=0$ has no real solutions, the complex solutions are $x_{1,2}=\pm 2\mathrm {i}$

The case $a\,c=0$ and because of $a\neq 0$ therefore $c=0\,$ , i.e. a double solution, exists only for equations of the type $ax^{2}=0$ with $a\neq 0$ and it is $x_{1,2}=0$ .

Missing constant link

From the equation $ax^{2}+bx=0$ by bracketing. x(ax+b)=0 , i.e., x=0 or must ax+b=0 hold. The two solutions are therefore

$x_{1}=0$ and $x_{2}=-{\tfrac {b}{a}}\ .$

For example, the equation $3x^{2}-2x=0$ has solutions $x_{1}=0$ and $x_{2}={\tfrac {2}{3}}\ .$

Equation in vertex form

The vertex shape

$a(x-d)^{2}+e=0$

is a variation of the pure quadratic equation $ax^{2}+c=0$ . Like the latter, it can be solved by "backward arithmetic": First subtract and divide by . This leads to

$(x-d)^{2}=-{\frac {e}{a}}\ .$

For $-{\frac {e}{a}}\geq 0$ it follows that

$x-d=\pm {\sqrt {-{\frac {e}{a}}}}$

By adding we get the solutions

$x_{1}=d+{\sqrt {-{\frac {e}{a}}}}$ and $x_{2}=d-{\sqrt {-{\frac {e}{a}}}}\ .$

For $-{\frac {e}{a}}<0$ we get the two complex solutions accordingly

$x_{1}=d+\mathrm {i} {\sqrt {\frac {e}{a}}}$ and $x_{2}=d-\mathrm {i} {\sqrt {\frac {e}{a}}}\ .$

Example:

${\begin{aligned}3(x-2)^{2}-5&=0&&|+5;:3\\(x-2)^{2}&={\frac {5}{3}}&&|\pm {\sqrt {\ }}\\x-2&=\pm {\sqrt {\frac {5}{3}}}&&|+2\\x&=2\pm {\sqrt {\frac {5}{3}}}\end{aligned}}$

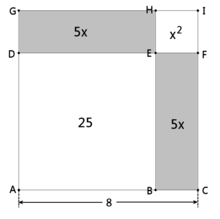
Solve with quadratic complement

When solving with quadratic addition, the binomial formulas are used to take a quadratic equation in general or normal form to the vertex form, which can then be easily solved.

One uses the first or second binomial formula in the form $(x\pm d)^{2}=x^{2}\pm 2dx+d^{2}\ .$

To do this, the quadratic equation is transformed so that the left side has the form $x^{2}\pm 2dx$ Then d^2 added to both sides. This is the "quadratic addition". The left-hand side now has the form $x^{2}\pm 2dx+d^{2}$ and can be transformed by the binomial formula to $(x\pm d)^{2}$ Then the equation is in the vertex form which is easy to solve.

This is best explained with a concrete numerical example. The following quadratic equation is considered

$3x^{2}-15x+18=0\ .$

First, the equation is normalized by dividing by the conductance coefficient (here 3):

$x^{2}-5x+6=0\ .$

The constant element (here 6) is subtracted on both sides:

$x^{2}-5x=-6\ .$

Now follows the actual quadratic addition: The left side must be completed in such a way that a binomial formula (here the second one) can be applied backwards. The from the binomial formula above is then ${\tfrac {5}{2}}$ , so on both sides of the equation must be $d^{2}=\left({\tfrac {5}{2}}\right)^{2}$ added:

$x^{2}-5x+\left({\frac {5}{2}}\right)^{2}=\left({\frac {5}{2}}\right)^{2}-6\ .$

The left side is transformed according to the binomial formula, the right side is simplified:

$\left(x-{\frac {5}{2}}\right)^{2}={\frac {1}{4}}\ .$

This leads to

$x-{\frac {5}{2}}=\pm {\frac {1}{2}}$ ,

so to the two solutions $x_{1}={\frac {5}{2}}+{\frac {1}{2}}=3$ and $x_{2}={\frac {5}{2}}-{\frac {1}{2}}=2\ .$

General solution formulas

One can also solve quadratic equations by using one of the general solution formulas derived using quadratic addition.

Solution formula for the general quadratic equation (a-b-c formula)

The solutions of the general quadratic equation $ax^{2}+bx+c=0$ are:

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ .$

The formula is colloquially called the "midnight formula" in parts of Germany and Switzerland because students are supposed to be able to recite it even if you wake them up at midnight and ask them for the formula. In Austria, the expression große Lösungsformel is commonly used.

Alternative forms

Alternative formulations of the a-b-c formula, more similar to the p-q formula discussed below, are:

$x_{1,2}={\frac {-b}{2a}}\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}=-{\frac {\ b}{2a}}\pm {\sqrt {\left(-{\frac {\ b}{2a}}\right)^{2}-{\frac {c}{a}}}}\$

If you write the quadratic equation in the form

$ax^{2}+2\beta x+c=0$

(i.e. with β $\beta =b/2$ ), the somewhat simpler solution formula is obtained:

$x_{1,2}={\frac {-\beta \pm {\sqrt {\beta ^{2}-ac}}}{a}}$

By extending the a-b-c formula with the term $-b\mp {\sqrt {b^{2}-4ac}}$ you get a formula which is also a=0 applicable for the linear case the case c=0 the calculation of the solution $x={\frac {-b}{a}}$ cannot be done because of a division by zero. In both cases, the solution formula is not needed anyway. However, for very small the alternative form is more robust to numerical cancellation.

$x_{1,2}={\frac {\left(-b\pm {\sqrt {b^{2}-4ac}}\right)\cdot \left(-b\mp {\sqrt {b^{2}-4ac}}\right)}{2a\cdot \left(-b\mp {\sqrt {b^{2}-4ac}}\right)}}={\frac {2c}{-b\mp {\sqrt {b^{2}-4ac}}}}$

Solution of the a-b-c formula with negative discriminant

If the discriminant $D=b^{2}-4ac$ introduced above is negative, the root of a negative number must be calculated for the solutions. In the number domain of the real numbers there are no solutions for this. In the complex number domain, ${\sqrt {D}}=i{\sqrt {-D}}$ . This term determines the imaginary part of the two conjugate solutions, once with positive sign, once with negative sign. The term before with $-{\tfrac {b}{2a}}$ becomes the constant real part of the two solutions:

$x_{1,2}=-{\frac {b}{2a}}\pm i\cdot {\frac {\sqrt {4ac-b^{2}}}{2a}}$ (complex case with negative discriminant).

$x_{1,2}=-{\frac {\ b}{2a}}\pm i\cdot {\sqrt {{\Big |}\left(-{\frac {\ b}{2a}}\right)^{2}-{\frac {c}{a}}{\Big |}}}\ .$

Derivation of the a-b-c formula

From the general form, transforming by the method of quadratic addition yields:

${\begin{array}{rcll}ax^{2}+bx+c&=&0&|-c\\[1ex]ax^{2}+bx&=&-c&|{}\cdot 4a\\[1ex]4a^{2}x^{2}+4abx&=&-4ac&|+b^{2}{\text{ (quadratische Ergänzung)}}\\[1ex](2ax)^{2}+2\cdot 2ax\,b+b^{2}&=&b^{2}-4ac&|{\text{ Umformen mit binomischer Formel}}\\[1ex](2ax+b)^{2}&=&b^{2}-4ac&|\pm {\sqrt {\quad }}\\[1ex]2ax+b&=&\pm {\sqrt {b^{2}-4ac}}&|-b\\[1ex]2ax&=&-b\pm {\sqrt {b^{2}-4ac}}&|:(2a)\\[1ex]x&=&{\dfrac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}&\end{array}}$

Calculation example

Given is the quadratic equation

$x^{2}-x-1=0$ .

Here $a=1,b=-1$ and c=-1 . Substituting these values into the a-b-c formula, we get the solutions

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}={\frac {-(-1)\pm {\sqrt {(-1)^{2}-4\cdot 1\cdot (-1)}}}{2\cdot 1}}={\frac {1\pm {\sqrt {5}}}{2}}$ .

Solution formula for the normal form (p-q formula)

In the presence of the normal form $x^{2}+px+q=0$ the solutions are according to the p-q formula:

$x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$

In Austria, this formula is known as the small solution formula.

Solution of the p-q formula with negative discriminant

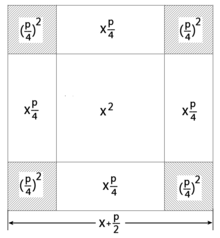
As with the a-b-c formula, if ${\tfrac {1}{4}}D=\left({\tfrac {p}{2}}\right)^{2}-q$ negative, there are no solutions in the number domain of the real numbers. The complex solutions are then given by:

$x_{1,2}=-{\frac {p}{2}}\pm i\cdot {\sqrt {q-\left({\frac {p}{2}}\right)^{2}}}$

Derivation of the p-q formula

The formula is obtained from the normal form of the quadratic equation by quadratic addition:

${\begin{array}{rcll}x^{2}+px+q&=&0&|-q\\[1ex]x^{2}+px&=&-q&|+\left({\dfrac {p}{2}}\right)^{2}{\text{ (quadratische Ergänzung)}}\\[1ex]x^{2}+2\cdot {\dfrac {p}{2}}\ x+\left({\dfrac {p}{2}}\right)^{2}&=&\left({\dfrac {p}{2}}\right)^{2}-q&|{\text{ binomische Formel}}\\[1ex]\left(x+{\dfrac {p}{2}}\right)^{2}&=&\left({\dfrac {p}{2}}\right)^{2}-q&|{\text{ Wurzel ziehen}}\\[1ex]\left|x+{\dfrac {p}{2}}\right|&=&{\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}&|{\text{ Betrag auflösen}}\\[1ex]x+{\dfrac {p}{2}}&=&\pm {\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}&|-{\dfrac {p}{2}}\\[1ex]x&=&-{\dfrac {p}{2}}\pm {\sqrt {\left({\dfrac {p}{2}}\right)^{2}-q}}\end{array}}$

Another way to derive the formula is to set in the a-b-c formula a=1 , b=p and c=q and draw the denominator 2 into the root.

Decomposition into linear factors

The solutions can be used to decompose the quadratic normalized polynomial into linear factors:

$x^{2}+px+q=(x-x_{1})\cdot (x-x_{2})$

and the non-standardized in

$ax^{2}+bx+c=a\cdot (x-x_{1})\cdot (x-x_{2})\ .$

Vieta set

If the quadratic equation is in normal form and has the solutions $x_{1}$ and $x_{2}$ , then

$0=x^{2}+px+q=(x-x_{1})\cdot (x-x_{2})=x^{2}-(x_{1}+x_{2})x+x_{1}x_{2}\ .$

By comparing coefficients, we obtain Vieta's theorem

$\,x_{1}+x_{2}=-p$ and $x_{1}\cdot x_{2}=q\ .$

In particular, if and are integers, the solutions can often be found quickly with some practice by trying out whether pairs of divisors of add up to For example, for $x^{2}+4x+3=0$ one obtains the solutions $x_{1}=-1$ and $x_{2}=-3$ by decomposing 3=(-1)(-3) with $(-1)+(-3)=-4\ .$

Numerical calculation

If the solutions are determined numerically and differ from each other by orders of magnitude, the problem of cancellation can be avoided by the following variation of the above formulas:

$x_{1}=-{\frac {p}{2}}-\operatorname {sgn}(p)\cdot {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$

$x_{2}={\frac {q}{x_{1}}}$

Here has $\operatorname {sgn}(p)$ the value for p<0 otherwise the value 1 {\displaystyle The first formula gives the largest-amount solution. The second formula is based on Vieta's theorem.

Examples

Calculation example

For the equation

$4x^{2}-12x-40=0$

the following solutions result according to the a-b-c formula

$x_{1,2}={\frac {-(-12)\pm {\sqrt {(-12)^{2}-4\cdot 4\cdot (-40)}}}{2\cdot 4}}$ ,

so $x_{1}=-2$ and $x_{2}=5\ .$

To use the p-q formula, the general form is first converted to normal form by dividing the equation by 4:

$x^{2}-3x-10=0\ .$

The p-q formula gives the solutions

$x_{1,2}=-{\frac {-3}{2}}\pm {\sqrt {\left({\frac {-3}{2}}\right)^{2}-(-10)}}$ ,

thus also $x_{1}=-2$ and $x_{2}=5\ .$

Using the decompositions $-10=(-2)\cdot 5$ and 5-2=3 we obtain the same solutions using Vieta's theorem.

More examples

$x^{2}+2x-35=0$
For the discriminant holds: the two real solutions $x_{1}=-7$ and $x_{2}=5\ .$
$x^{2}-4x+4=0$
The discriminant is . The (double) real solution is $x=2\ .$
$x^{2}+12x+37=0$
There are no real solutions, because the discriminant is negative. The complex solutions result in $x_{1}=-6+i$ and
$x_{2}=-6-i\ .$

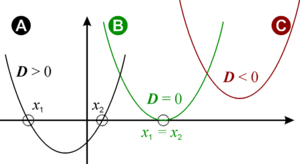
Position of the parabolas and effects on the number of zeros

Generalizations

Complex coefficients

The quadratic equation

$az^{2}+bz+c=0$

with complex coefficients $a,b,c\in \mathbb {C}$ , $a\neq 0$ always has two complex solutions $z_{1},z_{2}\in \mathbb {C}$ , which coincide exactly when the discriminant $b^{2}-4ac$ zero.

The solutions can be calculated as in the real case by quadratic addition or with the solution formulas given above. In general, however, a square root of a complex number must be calculated.

Example

For the quadratic equation

$z^{2}-(\mathrm {i} +1)z+\mathrm {i} =0$

the discriminant has the value $D=-2\mathrm {i} =(\mathrm {i} -1)^{2}$ . This gives the two solutions $z_{1}=1$ and $z_{2}=\mathrm {i} \ .$

Quadratic equations in general rings

In general, in abstract algebra, an equation of the form

$x^{2}+px+q=0$

with elements p, q of a body or ring is a quadratic equation. In solids and more generally in integrality domains it has at most two solutions, in arbitrary rings it can have more than two solutions.

If solutions exist, then they are also obtained in commutativerings with the p-q formula, if the characteristic of the ring is not equal to 2. Here, however, all possible square roots of the discriminant have to be considered. For a finite body $\mathbb {F} _{2^{n}}\cong \mathbb {F} _{2}(\varrho )$ of characteristic 2 one makes the approach $x=\textstyle \sum _{i=0}^{n-1}a_{i}\varrho ^{i}$ and arrives at a linear system of equations for the n coefficients from using i ϱ $x^{2}=\textstyle \sum _{i=0}^{n-1}a_{i}\varrho ^{2i}$ $\mathbb {F} _{2}$ .

Example

The quadratic equation

$x^{2}-1=0$

has in the residue class ring $\mathbb {Z} /8\mathbb {Z}$ the four solutions 1, 3, 5 and 7.

History

Already 4000 years ago in the Old Babylonian Empire problems were solved which are equivalent to a quadratic equation. For example, the clay tablet archived under the inventory number BM 34568 in the British Museum, according to the cuneiform translation succeeded by Otto Neugebauer in the 1930s, contains as the ninth problem the question of the side lengths of a rectangle, where the sum of length and width is 14 and whose area is equal to 48.

Although the solution path documented on the clay tablet does not reveal any reasoning, it does reveal intermediate values, as they also appear in the usual solution formula or equivalent geometric considerations:

"Length and width added is 14 and 48 is the area.
The sizes are not known. 14 times 14 (is) 196. 48 times 4 (is) 192.Subtract
192 from 196 and you are left with 4. What times what should
I take to (get) 4? 2 times 2 (is) 4. Subtract 2 from 14 and you are left with 12.
12 times ½ (is) 6. 6 is the width. To 2 you will add 6, 8 it is. 8 (is) the length."

- BM 34568#9, translation after Otto Neugebauer (1937). S. 18.

The intermediate values listed in the text, which are notated on the clay tablet in the Babylonian sexigesimal system, also result when the associated quadratic equation $x^{2}-14x+48=0$ is solved with the usual solution formula. Thereby the two solutions 8 and 6 are obtained, which geometrically correspond to the two side lengths of the rectangle:

$x_{1,2}={\frac {14\pm {\sqrt {196-192}}}{2}}={\frac {14\pm 2}{2}}\ .$

According to Høyrup, it can be assumed that the solution path followed by the Babylonians for the cited and similar tasks was geometrically motivated, as were the tasks themselves.

The ancient Greeks solved various geometrical problems that are equivalent to quadratic equations. For example, in Euclid's Elements one finds the problem:

"To divide a line so that the rectangle that makes the whole line with one part is equal to the square over the other part."

- Euclid: Elements. Volume II, Task 11

The task corresponds in today's notation to the equation

$a(a-x)=x^{2}$ ,

which can be transformed to the equation

$x^{2}+ax=a^{2}\ .$

In the book Brāhmasphuṭasiddhānta ("Perfection of the Teaching of Brahma") by the Indian scholar Brahmagupta, written around 628 AD, solution methods for quadratic equations were described verbally. Brahmagupta already used negative numbers and their calculation rules such as

"The product of a negative and a positive is negative, of two negatives is positive, of two positives is positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero."

- Brahmagupta: Brāhmasphuṭasiddhānta. Chapter XVIII, verse 33.

This enabled Brahmagupta to avoid case distinctions when he arrived at the quadratic equation, which today is known in the form

with $a{x}^{2}+bx=c$ $a,b,c\in \mathbb {R}$ and a>0

noted, described the following solution path:

"Using the mean [number] [meant: the coefficient of the unknowns, i.e., ], reduce the square root of the absolute value multiplied by four times the square [meant: coefficient unknowns] and increased by the square of the mean number; divide the remainder by twice the square [meant: coefficient ]. [The result] is the mean [number] [meant: the unknown ]"

- Brahmagupta, Brāhmasphuṭasiddhānta, Chapter XVIII, Verse 44.

This corresponds to the solution formula

$x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}\ .$

Like the "Arabic"-Indian numerals, the findings of the Indian scholars found their dissemination and further development via Islamic scientists. A particularly prominent role was played by the mathematician Al-Chwarizmi, whose book al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-ʾl-muqābala ("The Concise Book on Computational Procedures by Complementing and Equalizing"), written around 825 CE, contains for the first time general techniques for handling equations, albeit still described verbally. With the equivalent transformations of equations, which Al-Chwarizmi described in detail, any quadratic equation could be reduced to one of six types. Six types were necessary because Al-Chwarizmi, unlike Brahmagupta, did not use negative numbers.

Al-Chwarizmi's book contains a geometric solution procedure for all types by means of a numerical example, so that only positive solutions are possible. In the following list root means the searched solution and fortune means the square of the solution $x^{2}$ . Furthermore, a,b and denote non-negative coefficients:

As for the assets that are equal to the roots (today: $ax^{2}=bx$ ),
As for the assets that are equal to the number (today: $ax^{2}=c$ ),
As for the roots that are equal to a number (today: $bx=c$ ),
As for the assets and the roots, which are equal to the number (today: $ax^{2}+bx=c$ ),
As for the assets and the number equal to the roots (today: $ax^{2}+c=bx$ ) and
As for the roots and the number equal to the asset (today: $ax^{2}=bx+c$ ).

To solve the quadratic equations, al-Chwarizmi did not use equivalent transformations, i.e., algebraic reasoning, but geometric arguments, following the Greek tradition. As an example, the equation as it appears in al-Chwarizmi,

$x^{2}+10x=39$

can be solved $p,q>0$ as a special case of $x^{2}+px=q$ with (see figure). To do this, take the left side of the equation to be a square EFIH of side length (and thus area $x^{2}$ ) and two rectangles DEHG and BCFE with sides and (and thus area ), respectively. The square and the two rectangles are assembled into a gnomon with vertices BCIGDE as shown in the figure. This gnomon has an area of $x^{2}+10x=39$ . If we add the square ABED with side length (and therefore the area ) to the square ACIG , then this has the area 39+25=64 . On the other hand, this square ACIG by construction has side length 5+x and thus area $(5+x)^{2}$ . Because $64=8^{2}$ we conclude 5+x=8 and thus x=3 . The quadratic equation is thus "quadratically completed" to $(x+5)^{2}=64$ with the (positive) solution x=3 . Note that this geometric method does not give the negative solution x=-13

In Heron of Alexandria and also in al-Chwarizmi, the solution of

$ax^{2}+bx=c$

described verbally; in today's spelling as

$x={\frac {{\sqrt {ac+\left({\frac {b}{2}}\right)^{2}}}-{\frac {b}{2}}}{a}}\ .$

However, Heron adds the Euclidean way as a geometrical justification.

Around 1145 Robert of Chester and a little later Gerhard of Cremona translated the writings of al-Chwarizmi into Latin.

This brought the classification and geometric solution methods to Europe.

Michael Stiefel wrote the book Arithmetica integra in 1544 AD, which builds on the book Behend vnnd Hubsch Rechnung durch die kunstreichen regeln Algebre so gemeincklich die Coss genannt werden by Christoph Rudolff. The author manages to avoid the case distinction for quadratic equations by using negative numbers. But he does not allow negative numbers as solutions yet, because he considers them absurd.

A new approach to solving a quadratic equation was offered by Vieta's root theorem, published posthumously in 1615 in his work De Aequationem Recognitione et Emendatione Tractatus duo.

In 1637, René Descartes described a method for solving quadratic equations with a compass and ruler in his paper La Géométrie. He went on to show that equations of higher degree cannot generally be solved exclusively with compass and ruler.

Geometric solution of the equation according to Euclid $x^{2}+10x=39$

Geometric solution of the equation $x^{2}+px=q$ , as used by al-Chwarizmi to solve the equation $x^{2}+10x=39$ The area not shaded corresponds to .

Quadratic equation

General form - Normal form - Zero form

Solutions of the quadratic equation with real coefficients

Number of real zeros

Simple special cases

Missing linear element

Missing constant link

Equation in vertex form

Solve with quadratic complement

General solution formulas

Solution formula for the general quadratic equation (a-b-c formula)

Alternative forms

Solution of the a-b-c formula with negative discriminant

Derivation of the a-b-c formula

Calculation example

Solution formula for the normal form (p-q formula)

Solution of the p-q formula with negative discriminant

Derivation of the p-q formula

Decomposition into linear factors

Vieta set

Numerical calculation

Examples

Calculation example

More examples

Generalizations

Complex coefficients

Example

Quadratic equations in general rings

Example

History

See also

Search by letter