Pythagorean triple
In number theory, a Pythagorean triple or Pythagorean number triple is formed by three natural numbers that can occur as the lengths of the sides of a right triangle. With the lengths of the sides of such a triangle, a right angle can be constructed in a simple way, for example with the smallest triple 
. Because of the Pythagorean theorem, these triples are exactly the positive integer solutions of the Diophantine equation
.
If 
, 
and 
have no divisor in common except 1, then it is called a primitive Pythagorean triple.
Smallest triple:
History
Pythagorean triples are already found on Babylonian clay tablets dated to the Hammurabi dynasty (1829 to 1530 BC). The Plimpton 322 cuneiform tablet contains 15 different Pythagorean triples, including 
, 
and 
, suggesting that a method for computing such triples was known more than 3500 years ago. For Egypt, explicit mention of Pythagorean triples is known only from a Demotic papyrus of the 3rd century BC, but the use in particular of the triples and 
for slope angles on some pyramids dating from about two thousand years before the papyrus mentioned has also been discussed.
The Indian Baudhayana Sulbasutra from the 6th century BC contains five Pythagorean triples.
Pythagorean triples were treated by Euclid among the Greeks, by Pythagoras and Plato after Proclus's commentary on Euclid 's Elements, and later by Diophant .
The clay tablet Plimpton 322
Examples
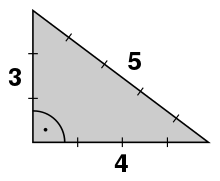
- is the smallest and best known Pythagorean triple. It is primitive because the three natural numbers have only 1 in common as a divisor. In the use of a twelve-knot cord, the proportions 3:4:5 for the side lengths can be used to span a right triangle and thus represent a right angle.
and 
are examples of other small primitive Pythagorean triples.- Examples of non-primitive Pythagorean triples are
with 
as a common divisor or 
with common divisor 
.
