Pythagorean theorem

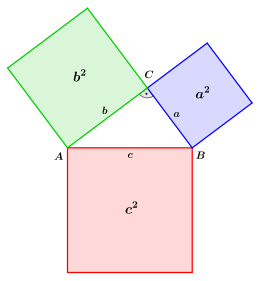
The Pythagorean Theorem (also known as the Hypotenuse Theorem) is one of the fundamental theorems of Euclidean geometry. It states that in all plane right triangles, the sum of the areas of the squares of the cathets is equal to the area of the square of the hypotenuse. If aand are bthe lengths of the sides adjacent to the right angle, the cathetus, and cis the length of the side opposite the right angle, the hypotenuse, then the theorem is expressed as an equation:

a^{2}+b^{2}=c^{2}

The theorem is named after Pythagoras of Samos, who is said to have been the first to find a mathematical proof for it, although this is disputed in research. The statement of the theorem was known in Babylon and India long before the time of Pythagoras, but there is no evidence that they had a proof there either.

Pythagorean theoremZoom
Pythagorean theorem

Mathematical statement

The Pythagorean theorem can be formulated as follows:

If a, band cthe side lengths of a right triangle, where aand b are the lengths of the cathets and c is the length of the hypotenuse, then a^{2}+b^{2}=c^{2}.

In geometrical interpretation, in a right triangle the sum of the areas of the two squares over the cathetes is equal to the area of the square over the hypotenuse.

The converse of the proposition is equally true:

If the equation a^{2}+b^{2}=c^{2} holds in a triangle with side lengths a, band c, then this triangle is right-angled, with the right angle copposite the side

Closely related to the Pythagorean Theorem are the Height Theorem and the Cathetus Theorem. These two theorems and the Pythagorean Theorem together form the Pythagorean Theorem Group. The cosine theorem described below is a generalization of the Pythagorean theorem.

Usage

Longitudes in a right triangle

From the Pythagorean theorem it follows directly that the length of the hypotenuse is equal to the square root of the sum of the squares of the cathets, thus

c={\sqrt {a^{2}+b^{2}}}.

A simple and important application of the theorem is to calculate the third side of a right triangle from two known sides. This is possible by transforming the equation for all sides:

\begin{align} a & = \sqrt{c^2 - b^2} \\ b & = \sqrt{c^2 - a^2} \end{align}

The inverse of the theorem can be used to test whether a given triangle is right-angled. This is done by testing whether the equation of the theorem for the sides is true for the given triangle. Thus, just knowing the side lengths of a given triangle is enough to conclude whether it is right-angled or not:

  • if the side lengths are 3, 4and 5, then 3^{2}+4^{2}=9+16=25=5^{2}, and therefore the triangle is right-angled.
  • if the side lengths are 4, 5and 6, then 4^2 + 5^2 = 16 + 25 = 41 \neq 6^2, and therefore the triangle is not right-angled.

From the Pythagorean theorem it follows that in a right triangle the hypotenuse is longer than each of the cathets and shorter than their sum. The latter also follows from the triangle inequality.

Pythagorean Triples

→ Main article: Pythagorean triple

Among all triples (a,b,c)satisfying the equation a^{2}+b^{2}=c^{2}, there are infinitely many where a, , band are ceach integers. These triples are called Pythagorean triples. The simplest of these triples consists of the numbers 3, 4and 5. Pythagorean triples have been used since ancient times to construct right triangles. An example is the twelve-knot cord used to lay a triangle whose sides have lengths 3, 4and 5. The two short sides then form a right angle.

The great Fermat theorem states that if the nnth n>2 power of a number cannot be represented as the sum of two powers of the same degree. What is meant are basic integers \neq 0and natural superscripts. Generally speaking, this means:

The equation a^{n}+b^{n}=c^{n}has n>2no solution for integer a,b,c \neq 0and natural numbers

This is surprising because for there n\leq 2are infinitely many solutions. For n=2 these are the Pythagorean number triples.

Euclidean distance

→ Main article: Euclidean distance

The Pythagorean Theorem provides a formula for the distance between two points in a Cartesian coordinate system. Given two points (x_0, y_0)and (x_1, y_1)in a plane, their distance is given cby

c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2}

given. This takes advantage of the fact that the coordinate axes are perpendicular to each other. This formula can also be extended to more than two dimensions and then provides the Euclidean distance. For example, in three-dimensional Euclidean space the following applies

c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2 + (z_1-z_0)^2}.

Questions and Answers

Q: What is the Pythagorean theorem?


A: The Pythagorean theorem is a statement about the sides of a right triangle.

Q: What angle is always equal to 90 degrees in a right triangle?


A: One of the angles of a right triangle is always equal to 90 degrees, which is referred to as the right angle.

Q: What are the two sides next to the right angle called?


A: The two sides next to the right angle are called the legs.

Q: What is the side opposite to the right angle called?


A: The side opposite to the right angle is called hypotenuse and it's always longest side.

Q: Is there an equation for calculating this theorem?


A: Yes, there is an equation for calculating this theorem which states that "the square of length of hypotenuse equals sum of squares of lengths of other two sides".

Q: Are all triangles with 90 degree angles considered "right" triangles?


A: No, not all triangles with 90 degree angles are considered "right" triangles; only those where one side (hypotenuse) is longer than other two sides and forms a 90 degree angle at its end can be classified as "right" triangles.

AlegsaOnline.com - 2020 / 2023 - License CC3