Product (mathematics)

A product is the result of a multiplication and also a term that represents a multiplication. The linked elements are called factors.

In this sense, a product is a representation of the form

$\cdot \;:\; A \times B \;\rightarrow\; C$

where one $b\in B$ usually $a\cdot b$ notates the product of $a\in A$ and

Derived from the Latin word producere meaning to produce, "product" originally denoted the result of multiplying two numbers (from Latin: multiplicare = to multiply). The use of the multiplication dot $\;\cdot\;$ goes back to Gottfried Wilhelm Leibniz, the alternative symbol $\times$ to William Oughtred.

Products of two numbers

Here, is always true. A = B = C , i.e., the product of two numbers is again a number. Products are here additionally assumed to be associative, i. e.

$(a\cdot b)\cdot c=a\cdot (b\cdot c)\quad {\text{für alle }}a,b,c\in A$

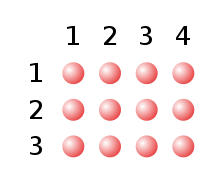
product of two natural numbers

For example, if you arrange tiles in a rectangular pattern in r rows of s tiles each, you will need

$r \cdot s = \sum_{i=1}^s r = \sum_{j=1}^r s$

Pieces. The multiplication here is a shorthand notation for the multiple addition of r summands (corresponding to the r rows), all of which carry the value s (there are s tiles in each row). But you can also calculate the total number by adding the number s (corresponding to the number of stones standing one behind the other in a column) r times in total (corresponding to the number r of such columns of stones standing side by side) (you need r-1 plus signs for this). This already shows the commutativity of the multiplication of two natural numbers.

If one counts the number 0 to the natural numbers, then these form a half ring. The inverse elements of the addition are missing for a ring: There is no natural number x with the property 3+x=0.

A product in which the number 0 appears as a factor always has the value zero: an arrangement of zero rows of tiles does not include a single tile, regardless of the number of tiles per row.

product of two integers

Adding the negative integers gives the ring $\mathbb {Z}$ of the integers. Two integers are multiplied by multiplying their respective amounts and adding the following sign:

${\begin{array}{|c|cc|}\hline \cdot &-&+\\\hline -&+&-\\+&-&+\\\hline \end{array}}$

In words, this table says:

Minus times minus equals plus
Minus times plus equals minus
Plus times minus equals minus
Plus times plus equals plus

For a strictly formal definition about equivalence classes of pairs of natural numbers compare the article about integers.

product of two fractions

In the integers you can add, subtract and multiply without restriction. Division by a non-zero number is possible only if the dividend is a multiple of the divisor. This restriction can be removed by moving to the body of rational numbers, that is, to the set $\mathbb {Q}$ of all fractions. The product of two fractions, unlike their sum, does not require the formation of a principal denominator:

$\frac{z}{n} \cdot \frac{z'}{n'} = \frac{z\cdot z'}{n\cdot n'}$

If necessary, the result can still be shortened.

product of two real numbers

As Euclid was already able to prove, there is no rational number whose square equals two. Likewise, the ratio of the circumference to the diameter of a circle, i.e. the circle number π, cannot be represented as a quotient of two integers. Both "gaps" are filled by a so-called completion in the transition to the body of real numbers $\mathbb {R}$ closed. Since an exact definition of the product does not seem possible in the brevity offered here, only a brief sketch of the idea is given:

Any real number can be thought of as an infinite decimal fraction. For example, ${\sqrt {2}}=1{,}4142\ldots$ and π $\pi =3{,}1415\ldots$ The rational approximations-such as 1.41 and 3.14-can be easily multiplied together. By successively increasing the number of decimal places, one obtains - in a process not feasible in finite time - a sequence of approximate values for the product ${\sqrt {2}}\cdot \pi =4{,}4428\ldots$

product of two complex numbers

Even over the set of real numbers there are unsolvable equations such as $x^{2}=-1$ . For both negative and positive values of , the square on the left-hand side is always a positive number. By transitioning to the body $\mathbb {C}$ of the complex numbers, which is often called adjunction, i.e. adding , the $\mathrm {i} ={\sqrt {-1}}$ so-called Gaussian number plane is formed from the real number straight line. Two points of this plane, i.e. two complex numbers, are formally multiplied considering : $\mathrm i^2=-1$

${\begin{aligned}(a+b\,{\mathrm i})\cdot (c+d\,{\mathrm i})&=a\cdot c+a\cdot d\,{\mathrm i}+b\cdot c\,{\mathrm i}+b\cdot d\cdot {\mathrm i}^{2}\\&=(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,{\mathrm i}\end{aligned}}$

Geometric interpretation

A complex number can also be written in plane polar coordinates:

$a + b\,\mathrm i = r \cdot ( \cos(\varphi) + \mathrm i \sin(\varphi) ) = r \cdot \mathrm e ^{\mathrm i \varphi}$

Is furthermore

$c + d\,\mathrm i = s \cdot ( \cos(\psi) + \mathrm i \sin(\psi) ) = s \cdot \mathrm e ^{\mathrm i \psi}$

then, due to the addition theorems for sine and cosine, the following applies

$(a \cdot c - b\cdot d) + (a\cdot d + b\cdot c) \,\mathrm i = r\cdot s \cdot ( \cos(\varphi+\psi) + \mathrm i \sin(\varphi+\psi) ) = r\cdot s \cdot \mathrm e ^{\mathrm i (\varphi+\psi)}$

Geometrically this means: multiplication of the lengths with simultaneous addition of the angles.

product of two quaternions

Even the complex numbers can be extended algebraically. A real four-dimensional space, the so-called Hamiltonian quaternions $\mathbb H$ . The associated multiplication rules are detailed in the article Quaternion. Unlike the number spaces above, the multiplication of quaternions is not commutative, i.e., $a\cdot b$ and $b\cdot a$ are different in general.

3 times 4 equals 12

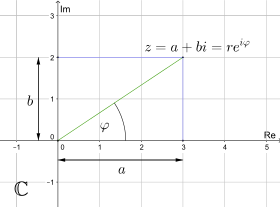
A complex number in polar coordinates

More examples of commutative rings

Remainder classes of integers

That the product of two numbers is odd exactly when both factors are odd is a widely known fact. Similar rules apply to divisibility by an integer N greater than two. Here, the even numbers correspond to the multiples of N; an even number is divisible by two without remainder. For the odd numbers, one should distinguish which remainder is left when this number is divided by N in whole numbers. Modulo 3 - according to the way of speaking - there are three remainder classes of integers: Those that are multiples of three, those with remainder 1, and those with remainder 2. The product of two such numbers always has remainder one modulo three.

The set of these residue classes, $\Z/N\Z$ , has exactly N elements. A typical element has the form $a+N\Z$ and represents the set of all integers which, when divided by N, give the same remainder as the number a. On the set of all such remainder classes is given by

$(a+N\Z) + (b+N\Z) = a+b + N\Z$

an addition and by

$(a+N\Z) \cdot (b+N\Z) = a\cdot b + N\Z$

explains a multiplication. The resulting ring is called the residue class ring modulo N. Precisely when N is a prime number, it is even a body. Example: modulo 5 the remainder class of 2 is inverse to that of 3, since 6 modulo 5 is one. The systematic finding of multiplicative inverses modulo N is done by means of the Euclidean algorithm.

Function rings

If the ring R is commutative, then the set forms $\mathbb {F} :=R^{M}$ (the set of all functions from a nonempty set M with values in R) also forms a commutative ring if addition and multiplication in $\mathbb F$ defined component-wise. That is, if one

$(f+g)(m):=f(m)+g(m)$

$(f\cdot g) (m) := f(m) \cdot g(m)$

for all $m\in M$ explained.

If one chooses as the ring R the real numbers $\mathbb {R}$ with the usual addition and multiplication, and as M approximately an open subset of $\mathbb {R}$ or more generally of $\mathbb {R} ^{n}$ , then the notions of continuity and differentiability of functions are meaningful. Then the set of continuous or differentiable functions $f:M\to R$ forms a subring of the function ring, which trivially must be commutative again if $\mathbb F$ or R is commutative.

Convolution product

→ Main article: Convolution (mathematics)

Let $f,g \colon \R \rightarrow \R\,$ two integrable real functions whose sums have a finite improper integral:

$\int \limits _{-\infty }^{\infty }|f(t)|\,\mathrm {d} \,t\;<\;\infty \quad {\text{und }}\int \limits _{-\infty }^{\infty }|g(t)|\,\mathrm {d} \,t\;<\;\infty$

Then the improper integral is

$(f*g) (t) \;:= \int\limits_{-\infty}^\infty f(\tau)\cdot g(t-\tau)\,\mathrm{d}\tau$

for each real number t is also finite. The function f*g defined in this way is called the convolution product or convolution of f and g. Thereby f*g is again integrable with finite improper magnitude integral. Furthermore, f*g=g*f, i.e., the convolution is commutative.

After Fourier transform, the convolution product is the point-wise defined product except for a constant normalization factor (so-called convolution theorem). The convolution product plays an important role in mathematical signal processing.

The Gaussian bell curve can be characterized by the fact that its convolution with itself again results in a bell curve that is somewhat stretched in width (cf. here). It is precisely this property that underlies the central limit theorem.

Polynomial Rings

The set $\R[X]$ of all polynomials in the variable X with real coefficients also forms a so-called polynomial ring. The product is calculated as follows:

$\left(\sum_{i=0}^n a_i X^i\right) \cdot \left(\sum_{j=0}^m b_j X^j\right) = \sum_{k=0}^{n+m} c_k X^k$

with

$c_k = \sum_{i+j=k} a_i \cdot b_j$

These rings play a major role in many areas of algebra. For example, the body of complex numbers can be elegantly defined formally as a factor ring $\R[X]/(X^2+1)$ .

In the transition from finite sums to absolutely convergent series or formal power series, the product discussed here becomes the so-called Cauchy product.

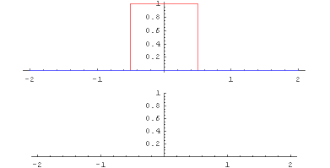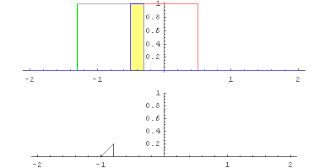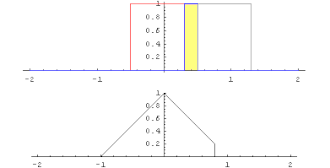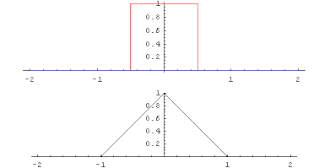
Convolution of the rectangular function with itself yields the triangular function