Probability density function

A probability density function, often called density function, probability density, distribution density, or just density for short, and abbreviated WDF or English pdf from probability density function, is a special real-valued function in stochastics, a branch of mathematics. There, the probability density functions are used for the construction of probability distributions using integrals as well as for the investigation and classification of probability distributions.

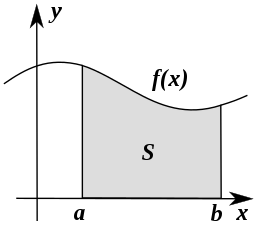
Unlike probabilities, probability density functions can also take values above one. The construction of probability distributions over probability density functions is based on the idea that the area between the probability density function and the x-axis from a point to a point corresponds to the probability of obtaining a value between and . Thus, it is not the functional value of the probability density function that is relevant, but the area under its function graph, i.e. the integral.

In a more general context, probability density functions are density functions (in the sense of measure theory) with respect to the Lebesgue measure.

While in the discrete case probabilities of events can be calculated by summing up the probabilities of the individual elementary events (for example, an ideal cube shows each number with a probability of $\tfrac 1 6$ ), this is no longer true for the continuous case. For example, two people are hardly exactly the same size, but only to within a hair's breadth or less. In such cases, probability density functions are useful. These functions can be used to determine the probability for any interval - for example, a height between 1.80 m and 1.81 m - even though there are infinitely many values in that interval, each of which has probability . $0$

The probability that a random variable takes a value between and corresponds to the content of the area under the graph of the probability density function .

Definition

Probability densities can be defined in two ways: once as a function from which a probability distribution can be constructed, the other time as a function derived from a probability distribution. The difference, then, is the direction of approach.

On the construction of probability measures

Given a real function

$f\colon \mathbb {R} \to \mathbb {R}$ , for which holds:

is nonnegative, that is, $f(x)\geq 0$ for all $x\in \mathbb {R}$ .
is integrable.
is normalized in the sense that

$\int _{-\infty }^{\infty }f(x)\,\mathrm {d} x=1$ .

Then is called a probability density function and defined by

$P([a,b]):=\int _{a}^{b}f(x)\,\mathrm {d} x$

a probability distribution on the real numbers.

Derived from probability measures

Given a probability distribution or a real-valued random variable .

If there exists a real function such that for all $a\in \mathbb {R}$

$P((-\infty ,a])=\int _{-\infty }^{a}f(x)\,\mathrm {d} x$

respectively

$P(X\leq a)=\int _{-\infty }^{a}f(x)\,\mathrm {d} x$

holds, then is called the probability density function of or of .

Examples

A probability distribution that can be defined by a probability density function is the exponential distribution. It has the probability density function

$f_{\lambda }(x)={\begin{cases}\displaystyle \lambda \mathrm {e} ^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}$

Here, λ $\lambda >0$ a real parameter. In particular, the probability density function for parameter λ $\lambda >1$ at the point x=0 exceeds the function value , as described in the introduction. That $f_{\lambda }(x)$ really a probability density function follows from the elementary integration rules for the exponential function, positivity and integrability of the exponential function are clear.

A probability distribution from which a probability density function can be derived is the continuous uniform distribution on the interval [0,1] . It is defined by

$P([a,b])=b-a$ for $a\leq b$ and $a,b\in [0,1]$

Outside the interval all events get the probability zero. We are now looking for a function for which

$\int _{a}^{b}f(x)\,\mathrm {d} x=P([a,b])=b-a$

holds if $a,b\in [0,1]$ . The function

$f(x)=1$

satisfies this. It is then continued outside the interval [0,1] by zero to integrate easily over any subset of the real numbers. A probability density function of the continuous uniform distribution would thus be:

$f(x)={\begin{cases}\displaystyle 1&{\text{ falls }}x\in [0,1]\\0&{\text{ sonst }}\end{cases}}$

Similarly, the probability density function would be

$f(x)={\begin{cases}\displaystyle 1&{\text{ falls }}x\in (0,1)\\0&{\text{ sonst }}\end{cases}}$

possible, since both differ only on a Lebesgue null set and both satisfy the requirements. One could create any number of probability density functions just by modifying the value at a point. In fact, this does not change the property of the function being a probability density function, since the integral ignores these small modifications.

For more examples of probability densities, see the list of univariate probability distributions.

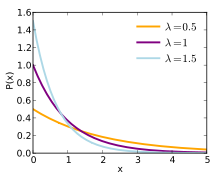
Probability density functions of the exponential distribution for different parameters.

Questions and Answers

Q: What is a probability density function?

A: A probability density function is a function that characterizes any continuous probability distribution.

Q: How is the probability density function of a random variable X written?

A: The probability density function of X is sometimes written as f_X(x).

Q: What does the integral of the probability density function represent?

A: The integral of the probability density function represents the probability that a given random variable with the given density is contained in an interval provided.

Q: Is the probability density function always non-negative throughout its domain?

A: Yes, by definition, the probability density function is non-negative throughout its domain.

Q: Does integrating over an interval sum up to 1?

A: Yes, integrating over an interval sums up to 1.

Q: What type of distribution does a Probability Density Function characterize?

A: A Probability Density Function characterizes any continuous probability distribution.