Prime number

$\mathbb P$

A prime number (from Latin numerus primus 'first number') is a natural number that is greater than 1 and exclusively divisible by itself and by 1. Here, primus specifically means "beginning, the first (of things)", so that an "initial number" is meant that cannot be constructed multiplicatively from any other (preceding) number.

The set of prime numbers is usually denoted by the symbol $\mathbb P$ . Associated with $\mathbb P$ is associated with the sequence $\left(p_{n}\right)_{n\in \mathbb {N} }$ of the primes ordered by their size, which is also called the prime sequence. It is therefore

$\mathbb {N} \supset \mathbb {P} =\{p_{n}\mid n\in \mathbb {N} \}$

with

$\left(p_{n}\right)_{n\in \mathbb {N} }=\left(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,\dotsc \right)$ (sequence A000040 in OEIS).

The importance of the prime numbers $\mathbb P$ for many areas of mathematics is based on three conclusions from their definition:

Existence and uniqueness of the prime factorisation: Every natural number that is greater than 1 and is not itself a prime number can be written as a product of at least two primes. This product representation is unambiguous except for the order of the factors. The following serves as proof
Euclid's lemma: If a product of two natural numbers is divisible by a prime number, then at least one of the factors is divisible by it.
Prime numbers cannot be represented as the product of two natural numbers that are both greater than 1.

These properties are used in algebra for generalisations of the prime number concept.

A number that is the product of two or more prime factors is called composite. The number 1 is neither prime nor composite, which is related to its invertibility. All other natural numbers are one of the two, either prime (i.e. prime) or composite.

Even in ancient Greece, people were interested in prime numbers and discovered some of their properties. Although prime numbers have always exerted a great attraction on people since then, many questions concerning prime numbers are still unsolved today, including those that are more than a hundred years old and can be easily formulated. These include Goldbach's conjecture that every even number except 2 can be represented as the sum of two primes, and the conjecture that there are infinitely many prime twins (i.e. pairs of primes whose difference is equal to 2).

Prime numbers and their properties play a major role in cryptography because prime factors cannot really be found efficiently even with the advent of electronic calculating machines. On the other hand, these machines enable efficient encryption and, if you know the key, decryption of even long texts.

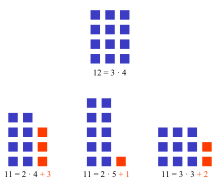
The number 12 is not a prime number, but the number 11 is.

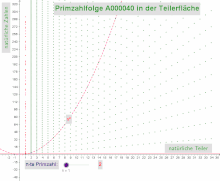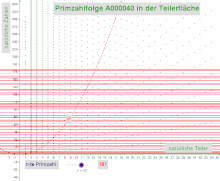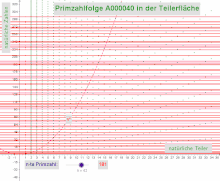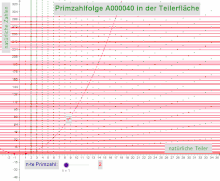
Prime number sequence in the divider surface

Properties of prime numbers

Within the set $\mathbb {N}$ of the natural numbers in that each of them has exactly two natural numbers as divisors.

With the exception of the number 2, all prime numbers odd, because all larger even numbers can be divided by (at least) 2 in addition to themselves and 1. Thus every prime number except 2 has the form 2k+1 with a natural number .

Each prime $p \neq 2$ assigned to one of the two classes "prime of the form 4k+1 " or "prime of the form 4k+3 ", where is a natural number. Each prime $p\neq 3$ can also be assigned to one of the two classes "prime of the form $3k+1$ form $3k+2$ , where is a natural number. Furthermore, any prime number has the p>3 form p = 6 p=6k+1 = 6 p=6k-1 where is a natural number. Furthermore, every prime number ends in $p>5$ one of the four decimal digits 1 , 3 1,3,7 {\displaystyle According to the Dirichlet prime number theorem, there are infinitely many primes in each of these classes.

Every natural number of the form 4m+3 with a non-negative integer contains at least one prime factor of the form 4k+3 . A corresponding statement about numbers of the form 4m+1 or prime factors of the form 4k+1 is not possible.

A prime number p>2 a,b written in the form a 2 + $a^{2}+b^{2}$ integers a , b exactly when p {\displaystyle form 4 k + 4k+1 two-square theorem). In this case, the representation is essentially unambiguous, i.e. except for the order and sign of a,b . This representation corresponds to the prime factorisation

$p=(a+b{\mathrm i})(a-b{\mathrm i})$

in the ring of whole Gaussian numbers.

The number -1 is a quadratic remainder modulo any prime number of the form 4k+1 and quadratic non-remainder modulo any prime number of the form 4k+3 .

Moreover, a prime number $p>3$ a,b written uniquely in the form a 2 + $a^{2}+3b^{2}$ integers a , b exactly when p {\displaystyle p} form 3 k +

If a number $2\leq p\leq {\sqrt {n}}$ n>1 any prime number 2 ≤ , then n {\displaystyle is prime number (see section Prime number tests and article Trial division).

The little theorem of Fermat

→ Main article: Small Fermatian theorem

Let be a prime number. For every integer which is not divisible by holds (for notation see congruence):

$a^{{p-1}}\equiv 1\mod p.$

For numbers not divisible by the following formulation is equivalent:

$a^{p}\equiv a\mod p.$

There are numbers which are not prime numbers but nevertheless behave like prime numbers to a base , i.e. it is $a^{n-1}\equiv 1{\bmod {n}}$ . Such are called Fermatian pseudoprimes to base . An which is a Fermat pseudoprime with respect to all bases alien to it is called a Carmichael number.

In this context, the problem of Fermatian pseudoprimes becomes apparent: they are mistaken for prime numbers by a prime number test that uses Fermat's small theorem (Fermatian prime number test). However, if an encryption method such as RSA uses a composite number instead of a prime number, the encryption is no longer secure. Therefore, better prime number tests must be used for such procedures.

Euler and the Legendre Symbol

A simple consequence of Fermat's little theorem is the following statement: For every odd prime number and every integer which is not divisible by , either

$a^{{{\frac {p-1}{2}}}}\equiv 1\mod p$

$a^{{{\frac {p-1}{2}}}}\equiv -1\mod p.$

One can show that the first case occurs exactly when there is a square number $m^{2}$ congruent to modulo }, see Legendre symbol.

Binomial coefficient

For primes and

$p\,{\Big |}{p \choose k};$

together with the binomial theorem it follows

$(a+b)^{p}\equiv a^{p}+b^{p}\mod p.$

For integers a,b this statement also follows directly from Fermat's little theorem, but it is also applicable, for example, to polynomials with integer coefficients; in the general context it corresponds to the fact that the mapping $x\mapsto x^{p}$ in rings of characteristic is a homomorphism, the so-called Frobenius homomorphism.

From Wilson's theorem ( is a prime number if and only if $(p-1)!\equiv -1{\pmod p}$ ) it follows that for every prime number and every natural number the congruence

${{np-1} \choose {p-1}}\equiv 1{\pmod {p}}$

is fulfilled.

Charles Babbage proved in 1819 that for every prime number p>2 congruence holds:

${{2p-1} \choose {p-1}}\equiv 1{\pmod {p^{2}}}$

The mathematician Joseph Wolstenholme (1829-1891) then proved in 1862 that for every prime $p>3$ following congruence holds:

${{2p-1} \choose {p-1}}\equiv 1{\pmod {p^{3}}}$

Giuga

From Fermat's little theorem it follows that for a prime number holds:

$1^{p-1}+2^{p-1}+\dotsb +(p-1)^{p-1}\equiv -1{\pmod {p}}$

Example p=5 :

$1^{4}+2^{4}+3^{4}+4^{4}=1+16+81+256=354=71\cdot 5-1\equiv -1{\pmod {5}}$

Giuseppe Giuga assumed that the reverse conclusion also applies, i.e. that a number with this property is always prime. It has not been clarified whether this assumption is correct. It is known, however, that a counterexample would have to have more than 10,000 decimal places. In connection with Giuga's conjecture, the Giuga numbers are examined.

Linear recursions

Fermat's little theorem can also be read in the form: In the sequence $a^{n}-a$ the -th sequence member for a prime number is always divisible by Similar properties are possessed by other sequences of exponential character, such as the Lucas sequence ( $p\mid L_{p}-1$ ) and the Perrin sequence ( $p\mid P_{p}$ ). For other linear recursions, analogous but more complicated statements hold, for example for the Fibonacci sequence $(f_{n})_{n=0,1,2,\dotsc }=0,1,1,2,3,5,\dotsc$ If a prime number, then divisible $f_{p}-{\Big (}{\frac p5}{\Big )}$ by ; where

${\Big (}{\frac p5}{\Big )}={\begin{cases}1&p\equiv 1,4\mod 5\\-1&p\equiv 2,3\mod 5\\0&p=5\end{cases}}$

the Legendre symbol.

Divergence of the sum of the reciprocals

→ Main article: Euler's theorem (prime numbers)

The series of reciprocals of the prime numbers is divergent. Thus applies:

$\sum _{i=1}^{\infty }{\frac {1}{p_{i}}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\dotsb =\infty$ .

This is equivalent to saying that the sequence $\textstyle a_{n}=\sum _{i=1}^{n}{\frac {1}{p_{i}}}$ defined by has no finite limit, which in turn means that for a sufficiently large chosen any conceivable real number can be surpassed. This is perplexing at first, since the prime number gaps keep increasing on average. Mertens' theorem makes a statement about the exact growth behaviour of this divergent series.

Primality tests

→ Main article: Prime number test

Whether any natural number is prime can be found out with a prime number test. There are several such methods that rely on special properties of prime numbers. In practice, the Miller-Rabin test is most frequently used, which has an extremely short runtime but delivers false-positive results with a small probability. With the AKS prime number test, it is possible to decide on the primality without risk of error in polynomial running time. However, in practice it is significantly slower than the Miller-Rabin test.

Prime certificate

Finding out whether a natural number is prime or not can be very time-consuming. For every prime number, however, a chain of assertions can be given, which are all directly comprehensible, together prove the primality and whose total length is at most proportional to the square of the length of the prime number. Such a proof is called a primality certificate.

In the case of the composite (non-primal) nature of a number, the difference between proof and finding a proof is even more obvious: Two factors whose product gives the composite number are sufficient as proofs; finding a real divisor, however, can take a lot of effort.

Largest known prime number

In the fourth century BC, the Greek Euclid logically concluded that there are an infinite number of prime numbers; this statement is known as Euclid's theorem. Euclid gave a contradictory proof of the correctness of this theorem (Elements, Book IX, § 20): Starting from the assumption that there are only finitely many prime numbers, another number can be constructed that has a previously unknown prime number as a divisor or is itself a prime number, which is a contradiction of the assumption. Thus, a finite set can never contain all prime numbers, so there are infinitely many. Today, we know a whole series of proofs for Euclid's theorem.

Euclid's theorem states that there is no largest prime number. However, there is no known method that efficiently generates arbitrarily large prime numbers - that is why there has always been one largest known prime number ever since people have been concerned with prime numbers. Currently (as of December 2018), it is $2^{82.589.933}-1,$ a number with 24,862,048 (decimal) digits, calculated on 7 December 2018. The discoverer Patrick Laroche received 3,000 US dollars for the find from the Great Internet Mersenne Prime Search project, which searches for Mersenne primes using distributed computing.

The largest known prime number was almost always a Mersenne prime, i.e. of the form $2^{n}-1,$ since in this special case the Lucas-Lehmer test can be applied, a very fast prime number test compared to the general situation. When searching for large prime numbers, therefore, only numbers of this or a similarly suitable type are examined for primality.

List of record primes by year

Number	Number of Decimal digits	Year	Discoverer (computer used)
²¹⁷⁻¹	6	1588	Cataldi
²¹⁹⁻¹	6	1588	Cataldi
²³¹⁻¹	10	1772	Euler
(²⁵⁹⁻¹)/179951	13	1867	Landry
²¹²⁷⁻¹	39	1876	Lucas
(²¹⁴⁸⁺¹)/17	44	1951	Ferrier
180·(²¹²⁷⁻¹)²⁺¹	79	1951	Miller & Wheeler (EDSAC1)
²⁵²¹⁻¹	157	1952	Robinson (SWAC)
²⁶⁰⁷⁻¹	183	1952	Robinson (SWAC)
^21.279−1	386	1952	Robinson (SWAC)
^22.203−1	664	1952	Robinson (SWAC)
^22.281−1	687	1952	Robinson (SWAC)
^23.217−1	969	1957	Trickle (BESK)
^24.423−1	1.332	1961	Hurwitz (IBM7090)
^29.689−1	2.917	1963	Gillies (ILLIAC 2)
^29.941−1	2.993	1963	Gillies (ILLIAC 2)
^211.213−1	3.376	1963	Gillies (ILLIAC 2)
^219.937−1	6.002	1971	Tuckerman (IBM360/91)
^221.701−1	6.533	1978	Noll & Nickel (CDC Cyber 174)
^223.209−1	6.987	1979	Noll (CDC Cyber 174)
^244.497−1	13.395	1979	Nelson & Slowinski (Cray 1)
^286.243−1	25.962	1982	Slowinski (Cray 1)
^2132.049−1	39.751	1983	Slowinski (Cray X-MP)
^2216.091−1	65.050	1985	Slowinski (Cray X-MP/24)
391581·2216^.193−1	65.087	1989	"Amdahl Six" (Amdahl 1200)
^2756.839−1	227.832	1992	Slowinski & Gage (Cray 2)
^2859.433−1	258.716	1994	Slowinski & Gage (Cray C90)
^{21.257.787−1}	378.632	1996	Slowinski & Gage (Cray T94)
^{21.398.269−1}	420.921	1996	Armengaud, Woltman (GIMPS, Pentium 90 MHz)
^{22.976.221−1}	895.932	1997	Spence, Woltman (GIMPS, Pentium 100 MHz)
^{23.021.377−1}	909.526	1998	Clarkson, Woltman, Kurowski (GIMPS, Pentium 200 MHz)
^{26.972.593−1}	2.098.960	1999	Hajratwala, Woltman, Kurowski (GIMPS, Pentium 350 MHz)
^{213.466.917−1}	4.053.946	2001	Cameron, Woltman, Kurowski (GIMPS, Athlon 800 MHz)
^{220.996.011−1}	6.320.430	2003	Shafer (GIMPS, Pentium 4 2 GHz)
^{224.036.583−1}	7.235.733	2004	Findley (GIMPS, Pentium 4 2.4 GHz)
^{225.964.951−1}	7.816.230	2005	Nowak (GIMPS, Pentium 4 2.4 GHz)
^{230.402.457−1}	9.152.052	2005	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
^{232.582.657−1}	9.808.358	2006	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
^{243.112.609−1}	12.978.189	2008	Smith, Woltman, Kurowski et al. (GIMPS, Core 2 Duo 2.4 GHz)
^{257.885.161−1}	17.425.170	2013	Cooper, Woltman, Kurowski et al. (GIMPS, Core2 Duo E8400 @ 3.00 GHz)
^{274.207.281−1}	22.338.618	2016	Cooper, Woltman, Kurowski et al. (GIMPS, Intel i7-4790 @ 3.60 GHz)
^{277.232.917−1}	23.249.425	2017	Jonathan Pace et al. (GIMPS, Intel i5-6600 @ 3.30 GHz)
^{282.589.933−1}	24.862.048	2018	Patrick Laroche et al. (GIMPS, Intel i5-4590T @ 2.0 GHz)

Distribution and growth

Pi function and prime number theorem

→ Main article: Prime number set

To examine the distribution of prime numbers, one considers, among other things, the function

$\pi \colon \mathbb {N} \to \mathbb {N} ,\;n\mapsto \pi (n)$ ,

which $\leq n$ specifies the number of prime numbers ≤ and is also called the prime number counting function. For example

$\pi (1)=0\ ;\ \pi (10)=4\ ;\ \pi (100)=25\ ;\ \pi (1000)=168;\ \pi (1000000)=78498$ .

This function and its growth behaviour is a popular subject of research in number theory. Over time, some approximation formulas have been developed and improved.

The prime number theorem states that

$\pi (x)\sim {\frac {x}{\ln x}}$

holds, i.e. the quotient of the left and right sides for $x\to\infty$ tends towards 1:

$\lim _{{x\to \infty }}{\frac {\pi (x)}{{\frac {x}{\ln x}}}}=1$ (see Asymptotic Analysis)

The Dirichlet prime number theorem, on the other hand, restricts the consideration to residue classes: Let be a natural number. If an integer which is not divisible from , then the arithmetic sequence

$a,a+m,a+2m,a+3m,\dotsc$

contain at most one prime number, because all sequence members are divisible by the greatest common divisor of and But if divisible by then Dirichlet's prime number theorem states that the sequence contains infinitely many primes. For example, there are infinitely many primes of the form 4k+1 and infinitely many of the form 4k+3 ( passes through each of the non-negative natural numbers).

This statement can be further specified in the following form: It applies

$\lim _{x\to \infty }{\frac {\#\{p\ \mid \ \mathrm {prim} ,\ p\leq x\ \mathrm {und} \ p\equiv a{\pmod {m}}\}}{\#\{p\ \mid \ \mathrm {prim} ,\ p\leq x\}}}={\frac {1}{\varphi (m)}};$

where φ $\varphi (m)$ the Eulerian phi function. In this sense, therefore, for a fixed in the residue classes $a+m{\mathbb Z}$ with ${\mathrm {ggT}}(a,m)=1$ each case "equally many" prime numbers.

Barriers

Bonse's inequality (proven) guarantees that the square of a prime number is smaller than the product of all smaller primes (from the fifth prime onwards).

According to the (unproven) Andrica's conjecture, the difference between the roots of the -th and the (n+1) -th prime is less than 1.

Prime number gaps

→ Main article: Prime number gap

The difference between two neighbouring prime numbers is called the prime number gap. This difference varies, and there are prime number gaps of any size. But there are also restrictions on the size of the gap depending on its location:

Bertrand's theorem ensures the existence of a prime number between any natural number and its double .

According to Legend's (unproven) conjecture, there is always at least one prime number between $n^{2}$ and $(n+1)^{2}$ .

Estimates of prime numbers and conclusions from the prime number theorem

In the following, let the sequence of prime numbers be denoted by $(p_{n})_{{n\in \mathbb{N} }}$ .

Assessments

For indices following estimates apply $n\in \mathbb {N}$

(1a)

$p_{n}<p_{{n+1}}<2\cdot p_{n}$

(1b)

${p_{{n+1}}}^{2}<2\cdot {p_{n}}^{2}$ ≥ $n\geq 5$

(1c)

$p_{n}<2^{n}$ ≥ $n \ge 2$

(1d)

$p_{n}>n\cdot \ln(n)$

(1e)

$\sum _{{k=2}}^{n}{{\frac {1}{p_{k}}}}>{\frac {1}{36}}\cdot {\ln {\ln(n+1)}}$ ≥ $n \ge 2$

Conclusions from the prime number theorem

The prime number theorem gives the following results:

(2a)

$\lim _{{n\rightarrow \infty }}{\frac {p_{{n+1}}}{p_{n}}}=1$

(2b)

${\frac {n}{\ln(n)-{\frac {1}{2}}}}<\pi (n)<{\frac {n}{\ln(n)-{\frac {3}{2}}}}$ 67 {\displaystyle $n\geq 67$

(2c)

For every positive real number there exists a sequence $(q_{n})_{{n\in \mathbb{N} }}$ of prime numbers with

$\lim _{{n\rightarrow \infty }}{\frac {q_{n}}{n}}=x$ .

(2d)

The set of quotients formed from all prime numbers is a dense subset of the set of all positive real numbers. I.e.: For any positive real numbers a,b with 0 < a < b always prime numbers p , q {\displaystyle , p,q such that

$a<{\frac {p}{q}}<b$

is fulfilled.

In the graph, the π $\pi$ function is shown in blue. The function $n/\ln(n)$ in green and the integral logarithm $\operatorname {Li} (n)$ red are approximations of the π $\pi$ function.

Generation of prime numbers

→ Main article: Prime number generator

One of the oldest algorithms for determining prime numbers is the sieve of Eratosthenes. To date, no efficient prime number generator is known. However, there are formulas for which there is a certain probability that the numbers generated are prime. Such numbers must be subsequently tested for their primality.

Illustration of the algorithm Sieve of Eratosthenes

Special prime numbers and prime number constellations

Prime number tuples
Ulam spiral

Other special types of prime numbers can be found in Category:Prime number.

Generalisation

In ring theory, the concept of prime is generalised to the elements of any commutative unitary ring. The corresponding terms are prime element and irreducible element.

The prime numbers and their negatives are then exactly the prime elements and also exactly the irreducible elements of the ring of integers. In factorial rings, i.e. rings with unique prime factorisation, the terms prime element and irreducible element coincide; in general, however, the set of prime elements is only a subset of the set of irreducible elements.

Especially in the number-theoretically significant case of Dedekind rings, prime ideals take on the role of prime numbers.

Prime factorisation

→ Main article: Prime factorisation

The fundamental theorem of arithmetic applies: Every integer greater than one can be represented as a product of prime numbers, and this representation is unambiguous except for the order of the factors. They are called the prime factors of the number.

Because every natural number greater than zero can be represented by multiplying prime numbers, the prime numbers occupy a special atomic position in mathematics; in a sense, they "generate" all other natural numbers - one as an empty product. Alexander K. Dewdney described them as largely similar to the elements of chemistry.

From this it also becomes clear why it is inexpedient to define one as a prime number: It is the neutral element of multiplication and thus cannot produce any other numbers multiplicatively. It is not needed for the representation of numbers as a product of prime factors. If one were to count 1 as a prime number, the uniqueness of the prime factorisation would be lost, because one can append any number of ones to any decomposition without changing the value of the number.

A number of factorisation methods have been developed to determine the prime factors of general numbers or numbers of special form as quickly as possible. However, there is as yet no known method for efficiently factorising arbitrary numbers, i.e. in a time that grows at most polynomially with the length of the given number. The factorisation assumption states that such a method does not exist either.

Prime numbers in computer science

Prime numbers play an important role in information security and especially in the encryption of messages (see cryptography). They are often used in asymmetriccryptosystems such as public key encryption methods. Important examples are the Diffie-Hellman key exchange, the RSA cryptosystem, which is used in OpenPGP, among others, the Elgamal cryptosystem and the Rabin cryptosystem. Here, the keys are calculated from large, randomly generated prime numbers that must remain secret.

Such algorithms are based on one-way functions that can be executed quickly, but whose inversion is practically impossible to calculate with the currently known technology. However, new information technologies, for example quantum computers, could change this. The unsolved P-NP problem is related to this.

Prime numbers in nature

Some animal and plant species (e.g. certain cicadas or spruces) reproduce particularly strongly in cycles of prime numbers (approximately every 11, 13 or 17 years) to make it more difficult for predators to adapt to the mass occurrence.

Why 1 is not a prime number

For hundreds of years, mathematicians have been discussing whether the number n=1 is a prime number or not. The important mathematician Godfrey Harold Hardy, for example, called the number 1 a prime number as late as 1908, but no longer so by 1929 at the latest. In general, since the 20th century, most mathematicians have agreed that the number 1 should not be counted as a prime number.

The argument for 1 being a prime number is the following:

1 is only divisible by itself and 1.

Arguments against 1 not being a prime number are the following:

A particularly important theorem in mathematics is the uniqueness of prime factorisation. For example, if were a prime number, the composite number would have $x=6$ many different prime factorizations, for example $x=6=2\cdot 3=1\cdot 2\cdot 3=1^{2}\cdot 2\cdot 3=\ldots =1^{657}\cdot 2\cdot 3=\ldots$ .

Suddenly, every number would have an infinite number of different prime factorizations and one would have to formulate the prerequisites for this important theorem differently so that unambiguity is given again. The ambiguity results specifically in this context from the fact that the number 1 is the neutral element of multiplication, which makes its use here nonsensical.

According to the definition, if you multiply two prime numbers together, you get a compositenumber, i.e. a number that consists of at least two (prime) factors. If 1 were a prime number, you could, for example, multiply it by a prime number and the product would again be a prime number and not a composite number. The definition of a composite number would therefore have to be much more complicated.
Every prime number has exactly two divisors: the number 1 and itself. has only one divisor and obviously does not fulfil this property, making this number different from all other primes.
The sieve of Eratosthenes would not work, because one would first have to delete all multiples of 1, which would leave no other number except 1.
For all primes the Eulerian Phi function φ $\varphi (p)=p-1$ . However, for φ $\varphi (1)=1\not =1-1=0$ . The theorem would therefore have to be reformulated and make 1 the exception.
For all primes the divisor function σ $\sigma _{0}(p)=2$ . But for σ $\sigma _{0}(1)=1\not =2$ . It is also true σ $\sigma _{1}(p)=p+1$ . But for σ $\sigma _{1}(1)=1\not =1+1=2$ . So the number 1 would be a big exception for this function(s) as well.
The definition of prime elements would have to be reformulated if 1 were a prime number. The new definition would be more complicated.
For every prime power there is a finite body that has exactly as many elements. If 1 were a prime number, there would also have to be a finite body with a single element. But this does not exist. You would have to change the definition of finite bodies.

There are other mathematical theorems about prime numbers that would also have to be reformulated if the number n=1 were a prime number.

The examples show that the set of prime numbers without a 1 is urgently needed - more urgently than the concept of prime numbers including the 1. Since there are always degrees of freedom in definitions, for the sake of economy of concepts, one has decided to exclude (besides the 0) the 1 (and somewhat more generally all units) from the prime numbers (or prime elements).

Questions and Answers

Q: What is a prime number?

A: A prime number is a natural number that cannot be divided by any other natural numbers except for 1 and itself.

Q: What is the smallest composite number?

A: The smallest composite number is 4, because 2 x 2 = 4.

Q: What are the next prime numbers after 2?

A: The next prime numbers after 2 are 3, 5, 7, 11, and 13.

Q: Is there a largest prime number?

A: No, there is no largest prime number. The set of prime numbers is infinite.

Q: What does the fundamental theorem of arithmetic state?

A: The fundamental theorem of arithmetic states that every positive integer can be written as a product of primes in a unique way.

Q: What is Goldbach's conjecture?

A: Goldbach's conjecture is an unsolved problem in mathematics which states that every even integer greater than two can be expressed as the sum of two primes.

Q: Who recorded proof that there was no largest prime number?

A: Euclid recorded proof that there was no largest prime number.