Polar coordinate system

This article deals with polar coordinates of the plane as well as the closely related cylindrical coordinates in space. For spatial polar coordinates see the article Spherical coordinates.

In mathematics and geodesy, a polar coordinate system (also: circular coordinate system) is a two-dimensional coordinate system in which each point in a plane is defined by the distance from a given fixed point and the angle to a fixed direction.

The fixed point is called the pole; it corresponds to the origin in a Cartesian coordinate system. The ray emanating from the pole in the specified direction is called the polar axis. The distance from the pole is usually denoted by ror ρ \rho and is called radius or radial coordinate, the angle is denoted by φ \varphi or θ \theta and is called angular coordinate, polar angle, azimuth or argument.

Polar coordinates are a special case of orthogonal curvilinear coordinates. They are useful when the relationship between two points can be described more easily by angles and distances than would be the case with x- and y-coordinates. In geodesy, polar coordinates are the most common method for measuring points (polar method). In radio navigation the principle is often called "Rho-Theta" (for distance and direction measurement).

In mathematics, the angular coordinate is measured in the mathematically positive direction of rotation (counterclockwise). If a Cartesian coordinate system is used at the same time, its coordinate origin usually serves as the pole and the xaxis as the polar axis. The angular coordinate is thus measured from the xaxis in the direction of the yaxis. In geodesy and navigation, the azimuth is measured clockwise from the north direction.

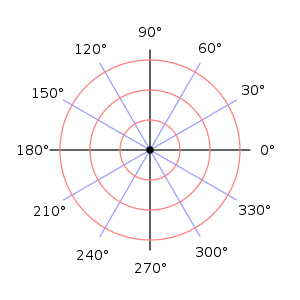
A polar grid of different angles with degreesZoom
A polar grid of different angles with degrees

History

The terms angle and radius were already used by the ancients in the first millennium BC. The Greek astronomer Hipparchus (190-120 BC) created a table of trigonometric chord functions to find the length of the chord for each angle. With this basis he was able to use polar coordinates to determine the position of certain stars. However, his work covered only a part of the coordinate system.

In his treatise On Spirals, Archimedes describes a spiral line with a function whose radius changes depending on its angle. However, the Greek's work did not yet include a full coordinate system.

There are different descriptions to define the polar coordinate system as part of a formal coordinate system. The whole history on this subject is summarized and explained in the book Origin of Polar Coordinates by the Harvard professor Julian Coolidge. According to it Grégoire de Saint-Vincent and Bonaventura Cavalieri introduced this conception independently of each other in the middle of the 17th century. Saint-Vincent wrote on the subject privately in 1625 and published his work in 1647, while Cavalieri published his elaboration in 1635, with a corrected version appearing in 1653. Cavalieri initially used polar coordinates to solve a problem concerning the area of the Archimedean spiral. Somewhat later, Blaise Pascal used polar coordinates to calculate the length of parabolic angles.

In the work Method of Fluxions (written 1671, published 1736), Sir Isaac Newton considers the transformation between polar coordinates, to which he referred as "Seventh Manner; For Spirals," and nine other coordinate systems.

He was followed by Jacob Bernoulli, who used a system consisting of a straight line and a point on this straight line, which he called polar axis or pole, in the technical journal Acta Eruditorum (1691). In it, the coordinates were defined by the distance from the pole and the angle to the polar axis. Bernoulli's work extended to the formulation of the circle of curvature of curves, which he expressed by the mentioned coordinates.

The term polar coordinates in use today was finally introduced by Gregorio Fontana and used in 18th century Italian writings. Subsequently, George Peacock adopted this term into the English language in 1816 when he translated the work of Sylvestre Lacroix Differential and Integral Calculus into his language.

Alexis-Claude Clairaut, on the other hand, was the first to think about polar coordinates in three dimensions, but it was the Swiss mathematician Leonhard Euler who succeeded in developing them.

Polar coordinates in the plane: circular coordinates

Definition

The polar coordinates of a point in the Euclidean plane (plane polar coordinates) are specified with respect to a coordinate origin (a point in the plane) and a direction (a ray starting at the coordinate origin).

The polar coordinate system is unambiguously defined by the fact that an excellent point, also called pole, forms the origin/zero point of the coordinate system. Furthermore, a ray emanating from it is distinguished as the so-called polar axis. Finally a direction (of two possible), which is perpendicular to this polar axis, must be defined as positive, in order to determine the sense of rotation / the direction of rotation / the orientation. Now an angle, the polar angle, can be defined between any ray passing through the pole and this distinguished polar axis. It is unique only up to integer revolutions around the pole, independently of what is chosen as angle measure for it. On the pole axis itself there is still an arbitrary but fixed scaling to define the radial unit length. 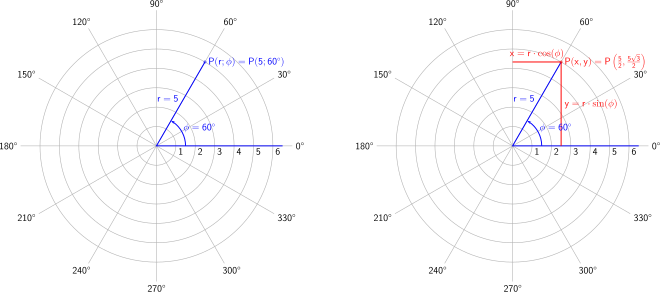Now each pair {\displaystyle (r,\phi )\in \mathbb {R} _{0}^{+}\times \mathbb {R} }can be uniquely assigned to a point in the plane, where the first component is considered to be the radial length and the second the polar angle. Such a pair of numbers is called (not necessarily unique) polar coordinates of a point in this plane.

Plane polar coordinates (with angles in degrees) and their transformation into Cartesian coordinates

The coordinate r, a length, is called radius (in practice also distance) and the coordinate ϕ \phi (polar) angle or, in practice (occasionally) also azimuth.

In mathematics, the counterclockwise angle is usually defined as positive when looking vertically at the plane (clock) from above. So the direction of rotation goes from right to top (and further to the left). As angle measure the radian is preferred as angle unit, because it is then analytically most elegant to handle. The polar axis typically points to the right in graphical representations of the coordinate system.

Conversion between polar coordinates and Cartesian coordinates

Conversion from polar coordinates to Cartesian coordinates

If one chooses a Cartesian coordinate system with the same origin as the polar coordinate system, thereby the xin the direction of the polar axis, and finally the positive y-axis in the direction of the positive sense of rotation - as shown in the figure above on the right -, the result is for the Cartesian coordinates xand ya point:

x=r\cos \varphi

y=r\sin \varphi

Conversion from Cartesian coordinates to polar coordinates

The conversion of Cartesian coordinates into polar coordinates is somewhat more difficult, because mathematically one always depends on a trigonometric inverse function (which does not cover the entire range of values of the solid angle). First, however, the radius rcan be calculated simply with the Pythagorean theorem as follows:

r=\sqrt{x^2 + y^2}

When determining the angle φ two peculiarities of polar coordinates must be taken into account\varphi :

  • For r = 0the angle φ is \varphi not uniquely determined, but could take any real value. For a unique transformation rule, it is often defined to be 0. The following formulas are r \ne 0given under the condition to simplify their derivation and presentation.
  • For r \ne 0the angle φ is 2\pi determined \varphi only to integer multiples of since the angles φ {\displaystyle\varphi and φ \varphi + 2\pi k(for k \in \Z) describe the same point. For the purpose of a simple and unambiguous transformation rule, the angle φ \varphi is 2\pi restricted to a half-open interval of length Usually, depending on the application, the intervals (-\pi ,\pi ]or [0,2\pi)chosen.

For the calculation of φ \varphi any of the equations

\cos \varphi = \frac x r; \quad \sin \varphi = \frac y r; \quad \tan \varphi = \frac y x

can be used. However, this does not uniquely determine the angle, even in the interval (-\pi ,\pi ]or [0,2\pi), because none of the three functions \sin , \cos and \tanis injective in these intervals. Moreover, the last equation is not defined for x=0Therefore, a case distinction is necessary which depends on which quadrant the point (x,y)is located in, that is, on the signs of xand y.

Calculation of the angle in the interval [-π, π] or [-180°,180°].

Using the arc tangent, φ can be calculated \varphi as follows in the interval (-\pi ,\pi ]or {\displaystyle (-180^{\circ },180^{\circ }]}can be determined:

{\displaystyle \varphi ={\begin{cases}\arctan {\frac {y}{x}}&\mathrm {f{\ddot {u}}r} \ x>0\\\left(\arctan {\frac {y}{x}}\right)+\pi &\mathrm {f{\ddot {u}}r} \ x<0,\ y\geq 0\\\left(\arctan {\frac {y}{x}}\right)-\pi &\mathrm {f{\ddot {u}}r} \ x<0,\ y<0\\+\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y>0\\-\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y<0\\\end{cases}}}

Some programming languages (such as Fortran 77) and application programs (such as Microsoft Excel) provide an {\displaystyle \operatorname {arctan2} (x,y)}with two arguments, which internally accounts for the case distinctions presented and ycomputes φ {\displaystyle\varphi for arbitrary values of xand

The same result is obtained if the point (x,y)in the Cartesian plane is considered as a complex number {\displaystyle z=x+\mathrm {i} y}and the angle

{\displaystyle \varphi =\arg(z)}

\arg calculated using the argument function

With the help of the arc cosine one gets along with only two case distinctions:

\varphi = \begin{cases} +\arccos\frac{x}{r} & \mathrm{f\ddot ur}\ y\geq 0\\ -\arccos\frac{x}{r} & \mathrm{f\ddot ur}\ y<0 \end{cases}

By taking advantage of the fact that in a circle a central angle is always twice as large as the corresponding circumferential angle, the argument φ can \varphi also be calculated using the arctangent function with fewer case distinctions:

\varphi ={\begin{cases}2\arctan {\frac {y}{r+x}}&{\mathrm {f{\ddot u}r}}\ r+x\neq 0\\\pi &{\mathrm {f{\ddot u}r}}\ r+x=0\end{cases}}

Calculation of the angle in the interval [0, 2π) or [0, 360°)

The calculation of the angle φ\varphi'the interval {\displaystyle[0,2\pi)or [0^\circ,360^\circ)can in principle be done in such a way that the angle is first calculated as described above in the interval (-\pi ,\pi ]calculated and, only if it is negative, is 2\pi increased by

\varphi' = \begin{cases} \varphi + 2\pi & \mathrm{falls}\ \varphi < 0\\ \varphi & \mathrm{sonst} \end{cases}

By modifying the first formula above, φ\varphi'[0,2\pi)determined directly in the interval as follows:

{\displaystyle \varphi '={\begin{cases}\arctan {\frac {y}{x}}&\mathrm {f{\ddot {u}}r} \ x>0,\ y\geq 0\\\arctan {\frac {y}{x}}+2\pi &\mathrm {f{\ddot {u}}r} \ x>0,\ y<0\\\arctan {\frac {y}{x}}+\pi &\mathrm {f{\ddot {u}}r} \ x<0\\\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y>0\\3\pi /2&\mathrm {f{\ddot {u}}r} \ x=0,\ y<0\\\end{cases}}}

The formula with the arc cosine gets along with only two case distinctions also in this case:

{\displaystyle \varphi '={\begin{cases}\arccos {\frac {x}{r}}&\mathrm {f{\ddot {u}}r} \ y\geq 0\\2\pi -\arccos {\frac {x}{r}}&\mathrm {f{\ddot {u}}r} \ y<0\end{cases}}}

Shifting the angle

In geodetic or other calculations, azimuths φ may differ \varphi with values outside the usual interval φ {\displaystyle \varphi _{\text{min}}\leq \varphi <\varphi _{\text{min}}+2\pi }lower limit φ {\displaystyle \varphi _{\text{min}}=0}(or else φ {\displaystyle \varphi _{\text{min}}=-\pi }) will result. The equation

{\displaystyle \phi =\varphi -2\pi \cdot {\bigl \lfloor }{\frac {\varphi -\varphi _{\text{min}}}{2\pi }}{\bigr \rfloor }}

shifts φ \varphi to the desired interval, so that ϕ{\displaystyle \phi \in \left[\varphi _{\text{min}},\,\varphi _{\text{min}}+2\pi \right)}holds. Here {\displaystyle x\mapsto \lfloor x\rfloor }the floor function rounding to the nearest integer, ⌊ \lfloor x\rfloor so for any real is xthe largest integer not greater than x

Functional determinant

From the conversion formulas from polar coordinates to Cartesian coordinates one obtains for the functional determinant as determinant of the Jacobi matrix:

{\displaystyle \det J=\det {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \varphi }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2}\varphi +r\sin ^{2}\varphi =r}

Area element

With the functional determinant, the result for the area element in polar coordinates is:

\mathrm dA = \mathrm dx\,\mathrm dy=|J|\,\mathrm dr\,\mathrm d\varphi = r\,\mathrm dr\,\mathrm d\varphi

As the accompanying figure shows, the area element can be interpreted as a differential rectangle with width {\displaystyle r\cdot \mathrm {d} \varphi }and height {\displaystyle \mathrm {d} r}.

Line element

From the above transformation equations

x=r \cos\varphi

y=r \sin\varphi

follow

\mathrm dx= \cos\varphi \, \mathrm dr - r \, \sin\varphi \, \mathrm d\varphi

\mathrm dy= \sin\varphi \, \mathrm dr + r \, \cos\varphi \, \mathrm d\varphi

The following applies to the Cartesian line element

\mathrm ds^2=\mathrm dx^2+\mathrm dy^2\,

for which in polar coordinates follows:

\mathrm ds^2=\mathrm dr^2+ r^2 \, \mathrm d\varphi^2

Velocity and acceleration in polar coordinates

For this purpose, the motion is decomposed into a radial and a perpendicular "transversal" component. For the velocity vector \dot {\vec r}following applies

\dot{\vec r}=\dot{r}\,\vec e_r + r\dot{\varphi}\,\vec e_\varphi

with unit vectors \vec e_r=(\cos(\varphi),\sin(\varphi))and \vec e_\varphi=({-\sin(\varphi)},\cos(\varphi)).

For the acceleration \ddot {\vec r}is valid

\ddot{\vec r}=(\ddot r - r\dot\varphi^2) \,\vec e_r+(2\dot r \dot \varphi + r \ddot \varphi) \,\vec e_{\varphi}.

Zoom


Zoom

Area element of width {\displaystyle r\cdot \mathrm {d} \varphi }and height {\displaystyle \mathrm {d} r}in polar coordinates.

Spatial polar coordinates: Cylinder coordinates and spherical coordinates

Cylinder coordinates

Cylinder coordinates or cylindrical coordinates are essentially plane polar coordinates with a third coordinate added. This third coordinate describes the height of a point vertically above (or below) the plane of the polar coordinate system and is generally zdenoted by The coordinate ρ \mathbf{\rho}now describes the distance of a point from the coordinate origin rather than from the z-axis.

Conversion between cylindrical coordinates and Cartesian coordinates

If you align a Cartesian coordinate system so that the zaxes coincide, the x\varphi =0points in the direction φ and the angle φ \varphi from the xaxis to the yincreases (is right-directed), then the following conversion formulas result:

x=\rho\,\cos\varphi

y=\rho\,\sin\varphi

{\displaystyle z=z}

For the conversion of Cartesian coordinates into cylindrical coordinates the same formulas result for ρ \rho and φ \varphi as for polar coordinates.

Basis vectors

\vec e_\rho = \frac{\frac{\partial \vec r}{\partial \rho}}{\left|\frac{\partial \vec r}{\partial \rho}\right|} = \begin{pmatrix} \cos\varphi \\ \sin\varphi \\ 0 \end{pmatrix},\quad \vec e_\varphi = \frac{\frac{\partial \vec r}{\partial \varphi}}{\left|\frac{\partial \vec r}{\partial \varphi}\right|} = \begin{pmatrix} -\sin\varphi \\ \cos\varphi \\ 0 \end{pmatrix},\quad \vec e_z = \frac{\frac{\partial \vec r}{\partial z}}{\left|\frac{\partial \vec r}{\partial z}\right|} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.

The basis vectors \vec e_\rho, \vec e_\varphiand {\vec {e}}_{z}are orthonormal to each other and form a right system in this order.

Functional determinant

The addition of the rectilinear coordinates znot affect the functional determinant:

{\displaystyle \det {\frac {\partial (x,y,z)}{\partial (\rho ,\varphi ,z)}}={\begin{vmatrix}\cos \varphi &-\rho \sin \varphi &0\\\sin \varphi &\rho \cos \varphi &0\\0&0&1\end{vmatrix}}=\rho }

Consequently, for the volume element \mathrm {d} V:

\mathrm{d}V=\rho \,\mathrm{d}\rho\, \mathrm{d}\varphi \, \mathrm{d}z

This also corresponds to the square root of the amount of the determinant of the metric tensor, with the help of which the coordinate transformation can be calculated (see Laplace-Beltrami operator).

{\displaystyle {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}={\begin{pmatrix}\cos \varphi &-\rho \sin \varphi &0\\\sin \varphi &\rho \cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}\mathrm {d} \rho \\\mathrm {d} \varphi \\\mathrm {d} z\end{pmatrix}}}

{\displaystyle {\begin{pmatrix}\mathrm {d} \rho \\\mathrm {d} \varphi \\\mathrm {d} z\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}}

Vector Analysis

The following representations of the Nabla operator can be applied in the given form directly to scalar or vector-valued fields in cylindrical coordinates. The procedure is analogous to the vector analysis in Cartesian coordinates.

Gradient

The representation of the gradient transfers from Cartesian to cylindrical coordinates as follows:

{\displaystyle \nabla f={\frac {\partial f}{\partial \rho }}{\vec {e}}_{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\vec {e}}_{\varphi }+{\frac {\partial f}{\partial z}}{\vec {e}}_{z}}

Divergence

In the case of divergence, additional terms are added, resulting from the derivatives of the unit vectors depending on ρ \rho , φ \varphi and zdependent unit vectors:

{\displaystyle \nabla \cdot {\vec {A}}={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}(\rho A_{\rho })+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}}

Rotation

The representation of the rotation is as follows:

{\displaystyle \nabla \times {\vec {A}}=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\vec {e}}_{\rho }+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\vec {e}}_{\varphi }+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}(\rho A_{\varphi })-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\vec {e}}_{z}}

Spherical coordinates

→ Main article: Spherical coordinates

Spherical coordinates are essentially plane polar coordinates with a third coordinate added. This is done by specifying an angle θ\theta \in [0,\pi ]for the third axis. This third coordinate describes the angle between the vector {\vec {r}}to the point Pand the z-axis. θ \theta is zero exactly when Pon the z-axis.

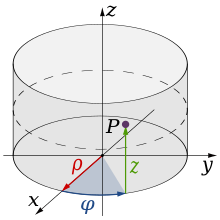
Cylinder coordinatesZoom
Cylinder coordinates

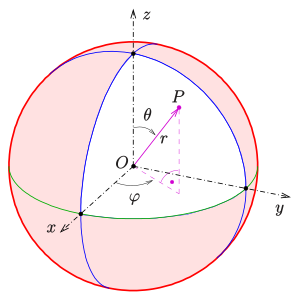
Spherical coordinatesZoom
Spherical coordinates

n-dimensional polar coordinates

It is also possible to give a generalization of polar coordinates with n \ge 3for an n-dimensional space with Cartesian coordinates {\displaystyle x_{i}\in \mathbb {R} }for i=1,\dotsc ,nspecify. For this purpose, one introduces for each new dimension (inductive construction over same) another angle \vartheta_{n-2}\in [0,\pi]which is the angle between the vector x\in \R^nand the new positive coordinate axis for x_{n}. With the same procedure the angular coordinate of the 2-dimensional space can be constructed {\displaystyle \varphi =\vartheta _{0}\in [0,\pi ]}inductively from the number line in a consistent way by means of φ provided that for the radial coordinate also negative values, thus whole \mathbb {R} would be allowed.

Conversion to Cartesian coordinates

A conversion rule from these coordinates to Cartesian coordinates would then be:

{\displaystyle {\begin{array}{lcr}x_{1}&=&r\ \cos \varphi \ \sin \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{2}&=&r\ \sin \varphi \ \sin \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{3}&=&r\ \cos \vartheta _{1}\ \sin \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{4}&=&r\ \cos \vartheta _{2}\ \cdots \ \sin \vartheta _{n-3}\ \sin \vartheta _{n-2}\\\vdots &\vdots &\vdots \qquad \qquad \qquad \quad \\x_{n-1}&=&r\ \cos \vartheta _{n-3}\ \sin \vartheta _{n-2}\\x_{n}&=&r\ \cos \vartheta _{n-2}\end{array}}}

As can be shown, these polar coordinates change into the ordinary polar coordinates for the case n=2and into the spherical coordinates for n=3

Functional determinant

The functional determinant of the transformation from spherical coordinates to Cartesian coordinates is:

{\displaystyle \det {\frac {\partial (x_{1},\dotsc ,x_{n})}{\partial (r,\vartheta _{1},\dotsc ,\vartheta _{n-2},\varphi )}}=r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}}

Thus, the n-dimensional volume element is:

{\displaystyle {\begin{matrix}\mathrm {d} V&=&r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}\mathrm {d} r\ \mathrm {d} \varphi \ \mathrm {d} \vartheta _{1}\dotsm \mathrm {d} \vartheta _{n-2}\\&=&r^{n-1}\ \mathrm {d} r\ \mathrm {d} \varphi \ \prod \limits _{j=1}^{n-2}(\sin \vartheta _{j})^{j}\ \mathrm {d} \vartheta _{j}\end{matrix}}.}

Note: n-dimensional cylindrical coordinates are simply a product / composition k-dimensional spherical coordinates and (n-k)-dimensional Cartesian coordinates with {\displaystyle k\geq 2}and {\displaystyle n-k\geq 1}.


AlegsaOnline.com - 2020 / 2023 - License CC3