AlegsaOnline.com

Pi (π): the circle constant and its role in mathematics

Pi (π) is the universal ratio of a circle's circumference to its diameter. An irrational, transcendental constant, it appears across geometry, analysis, probability and applied science.

Author: Leandro Alegsa Creation date: November 13, 2022 Last updated: June 22, 2026

simple.wikipedia.org · CC BY-SA 3.0

Overview

Pi (symbol: π) is the fixed number obtained by dividing the circumference of any circle by its diameter. That fixed relationship — the same for every circle — makes π a fundamental mathematical constant. Numerically it begins 3.141592653589793... and continues without repeating or terminating; this non-repeating decimal behavior is one of the defining characteristics of π.

Key properties

Several concise facts summarize the nature of π. It is the ratio C/d where C is the circumference and d the diameter of a circle. π is irrational, meaning it cannot be expressed exactly as a fraction of two integers, and it is also transcendental, which places further restrictions on algebraic equations it can satisfy. Decimal expansions of π contain no repeating block of digits, so approximations and symbolic formulas are often used in calculations.

Formulas and commonly used approximations

Pi appears in basic geometric formulae and in many deeper identities. Two of the most familiar geometric formulas are:

Circumference: C = 2πr, where r is the circle radius.
Area: A = πr².

Analytic and infinite expressions for π include series and products used in analysis and computation. A well-known alternating series is the Gregory–Leibniz formula for π/4 = 1 − 1/3 + 1/5 − 1/7 + ... . Practical rational approximations used historically and today include 22/7 (simple and convenient) and 355/113 (remarkably accurate for a small fraction). Computers and algorithms compute π to very large numbers of digits for testing numerical methods and hardware.

History and development

The search for accurate values of π goes back to ancient civilizations. Mesopotamian and Egyptian sources used early approximations; Greek mathematicians developed geometric bounds. Notably, Archimedes used polygonal approximations to bound π between two values and is often credited with the first rigorous strategy for narrowing its range; see Archimedes for this approach. In the 18th and 19th centuries, continued advances in analysis connected π with infinite series, trigonometry and complex analysis. The use of the Greek letter π to denote the constant dates from the early 18th century and became standard through the work of later mathematicians.

Applications and significance

Beyond elementary geometry, π occurs across mathematics and the physical sciences. It appears in trigonometric functions, Fourier series, probability theory, the Gaussian integral (where √π appears), and in formulas describing waves, heat flow, electromagnetism and quantum mechanics. In probability, problems such as Buffon’s needle link geometric probability to π. Engineers and scientists use π in modeling, simulation and design, and high-precision digits of π are used to benchmark numerical algorithms and computers.

Distinctions and notable facts

Important mathematical distinctions include π’s irrationality and transcendence: the first means it cannot be written as p/q for integers p and q, and the second means it is not a root of any nonzero polynomial with rational coefficients. Transcendence of π also implies that classical compass-and-straightedge problems such as squaring the circle are impossible. Modern interest in π ranges from recreational memorization of digits to rigorous uses in analysis and numerical work. For further background on the concept and its many appearances, consult resources on geometry and mathematical constants via mathematical constants and introductions to ratio-based definitions, or detailed historical accounts linked to circumference and diameter. Detailed discussions of irrationality and proofs are available in texts about irrational numbers and the work of classical authors like Archimedes.

The Greek lowercase letter Pi is the symbol of the circle number.

History of the designation

The circular number and some of its properties were already known in ancient times.

The designation with the Greek letter Pi ( $\pi$ ) (after the initial letter of the Greek word περιφέρεια - to Latin peripheria, "peripheral area" or περίμετρος - perimetros, "circumference") was first used by William Oughtred in his 1647 paper Theorematum in libris Archimedis de Sphæra & Cylyndro Declaratio. In it he expressed by π $\tfrac{\pi}{\delta}$ the ratio of half the circumference (semiperipheria) to half the diameter (semidiameter), i.e. π $\tfrac{\pi}{\delta}= 3{,}1415\ldots$

The same terms were used around 1664 by the English mathematician Isaac Barrow.

David Gregory took π $\tfrac{\pi}{\rho}$ (1697) for the ratio of circumference to radius.

59 years later than Oughtred, in 1706, the Welsh mathematician William Jones was the first to use the lowercase Greek letter π to $\pi$ express the ratio of circumference to diameter in his Synopsis Palmariorum Matheseos.

It was not until the 18th century that π $\pi$ popularized by Leonhard Euler. He first used π $\pi$ for the circle number in 1737, having previously used . Since then, due to Euler's importance, this designation has been in common use.

Definition

Several equivalent approaches exist to define the circle number π . $\pi$

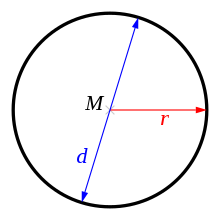
The first (classical!) definition in geometry is that according to which the circle number is a ratio numerically equal to the quotient π $\pi ={\tfrac {U}{d}}$ formed from the circumference a circle and the associated diameter second approach to geometry is related to this and consists in understanding by the circle number the quotient π $\pi ={\tfrac {A}{r^{2}}}$ formed by the area a circle and the area of a square constructed over a radius (of length ). (This radius is called the radius of the circle. ) This second definition is expressed by the proposition that the area of a circle is π of the $\pi :4$ surrounding square.

In analysis, one often proceeds (after Edmund Landau) to first define the real cosine function $\cos(x)$ via its Taylor series and then to define the circle number as the double of the smallest positive zero of the cosine. Further analytical approaches go back to John Wallis and Leonhard Euler.

Questions and Answers

Q: What is the number π?

A: π is a mathematical constant that is the ratio of a circle's circumference to its diameter.

Q: What does this produce?

A: This produces a number, and that number is always the same.

Q: How does this number start?

A: The number starts as 3.141592653589793... and continues without end.

Q: What type of numbers are these?

A: These numbers are called irrational numbers.

Q: What is the diameter of a circle?

A: The diameter of a circle is the largest chord which can be fitted inside it, passing through its center.

Q: What is the circumference of a circle? A: The distance around a circle is known as its circumference.

Q: Does pi remain constant regardless of different circles? A: Yes, pi remains constant regardless of different circles because the relationship between their circumference and diameter always stays the same.