Phase velocity

The phase velocity is the propagation velocity of equal phases of a monochromatic wave.

In dispersive media, waves of different frequencies propagate with different phase velocities. Consequently, when wave packets (i.e. the sum of several superimposed monochromatic waves) propagate in dispersive media, the phase differences between individual components are not constant but time-dependent: The shape of the wave packet changes (it "dissipates").

In the upper figure, the red dot moves with the phase velocity. In the second figure, a wave packet is shown whose group velocity is equal to the phase velocities of the individual components. In the third figure, the phase velocities of the individual components are different.

The phase velocity $v_{{\mathrm {p}}}$ calculated from the wavelength λ $\lambda\,$ (the distance traveled) and the period $T\,$ (the time needed for this) to become

$v_{{\mathrm {p}}}={\frac {\lambda }{T}}.$

Based on the definitions of frequency $f\,$ , angular frequency ω $\omega \,$ and angular wavenumber $k\,$ results in the equivalent representation

$v_{{\mathrm {p}}}=\lambda \cdot f={\frac {\omega }{k}}.$

The speed of light in a vacuum is the upper limit for the transmission speed of energy and information. However, there are numerous cases where phase velocities above the speed of light occur. Examples are matter waves and waves in waveguides.

A wave packet propagates in a dispersive medium.

A wave packet propagates in a non-dispersive medium (e.g. an electromagnetic wave in a vacuum).

The red dot is always at the point of the same phase (wave crest) and moves with the phase velocity of the blue, monochromatic wave.

The green points move at group speed, the red one at phase speed.

Relationship with group velocity and dispersion

Designation

Symbol

Relationships

Amplitude

${\vec A}_{0}$

${\vec {A}}_{0}\perp {\vec {k}}$	Transverse wave
${\vec {A}}_{0}\\|{\vec {k}}$	Longitudinal wave

Wave vector

${\vec {k}}$

Direction of propagation

Circular wave number

$k\,$

$k=|{\vec {k}}|$

Wavelength

$\mathbf {\lambda }$

$\lambda ={\frac {2\pi }{k}}$

Circular frequency

$\mathbf {\omega }$

$\mathbf {\omega } {\big (}{\vec {k}}{\big )}$ Dispersion relation

Frequency

$f={\frac {\omega }{2\pi }}$

Phase velocity

$v_{{\mathrm {p}}}$

$v_{\mathrm {p} }={\frac {\omega }{k}}=\lambda f$

Group speed

$v_{{\mathrm {g}}}$

$v_{\mathrm {g} }={\frac {\partial \omega }{\partial k}}$

Phase angle

$\varphi$

$\varphi ={\vec {k}}\cdot {\vec {r}}-\omega t$

For the mathematical description of a wave in a special medium, one needs its waveform, amplitude, frequency, phase angle and the associated wave equation - if necessary with boundary conditions. Nevertheless, different velocities can be assigned to such a clearly defined wave, which should not be confused with the phase velocity.

The speed at which a wave transmits energy or information is the signal speed. For a lossless medium, this is equal to the group velocity, i.e. the velocity of a wave packet. Such a wave packet is composed of monochromatic waves with different frequencies Each of these monochromatic waves has its own phase velocity:

$v_{{\mathrm {p}}}=v_{{\mathrm {p}}}(f)$ .

The functional relationship between phase velocity and frequency is called dispersion.

For electromagnetic waves, the phase velocity $v_{{\mathrm {p}}}$ and the group velocity $v_{{\mathrm {g}}}$ in vacuum is equal to the speed of light , i.e., the vacuum is nondispersive. In matter, on the other hand, the phase velocity generally depends on the frequency. Because of the relation for the refractive index } $n=c/v_{{\mathrm {p}}}$ , here the frequency dependence of the refractive index n(f) is called dispersion.

Examples

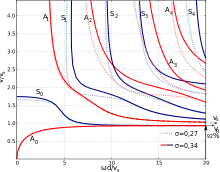
Structure-borne sound

In solids, sound waves can propagate as structure-borne sound. The phase velocities vary depending on the wave type. For example, the phase velocity of the longitudinal wave at room temperature in stainless steel is about 5980 m/s; the phase velocity of the transverse wave is smaller by a factor of about 1.8: approx. 3300 m/s. In thin plates, other types of waves exist, so-called Lamb waves. In the adjacent picture, each branch corresponds to a Lamb wave type (mode). Vertically, the phase velocity $v_{{\mathrm s}}$ shown in units of the transverse wave velocity , horizontally, the frequency is shown as the product of angular frequency ω $\omega$ and plate thickness in units of the transverse wave velocity. The higher modes $S_{1},A_{1},S_{2},A_{2},\dots$ exist only above certain minimum frequencies and then propagate at very high phase velocities. The $A_{0}$ mode has a vanishing phase velocity for small frequencies.

Matter wave

According to the wave-particle duality, a particle, e.g. an electron with energy and momentum , a wavelength λ $\lambda$ assigned and thus a phase velocity

$v_{{\mathrm p}}=f\lambda ={\frac {\omega }{k}}={\frac {E}{p}}$ .

With Einstein's formula

$E=mc^{2}$

or in the formulation with the Lorentz factor γ $\gamma$

$E=m_{0}\gamma c^{2}$

and the definition of the relativistic momentum $p=m_{0}\gamma v$ follows

$v_{{\mathrm p}}={\frac {m_{0}\gamma c^{2}}{m_{0}\gamma v_{{\mathrm g}}}}={\frac {c^{2}}{v_{{\mathrm g}}}}.$

Here the speed of light, the highest speed at which energy or information can propagate. The group velocity $v_{{\mathrm g}}={\frac {{\mathrm d}\omega }{{\mathrm d}k}}$ is the particle velocity, which is always less than Therefore

So the de Broglie phase velocity is always greater than the speed of light. This so-called superluminal velocity of matter waves does not contradict the theory of relativity, because the signal velocity $v_{{\mathrm g}}$ is

Waveguide

Electromagnetic waves in normal waveguides used for power transmission also travel at phase velocities above the speed of light. In the traveling wave accelerator, the phase velocity must be artificially reduced to values below the speed of light by regularly arranged conductive apertures.

Lambmodes for two different materials with Poisson's ratio
$\sigma =0{,}34$ (e.g. titanium) and σ $\sigma =0{,}27$ (e.g. steel)

Questions and Answers

Q: What is phase velocity?

A: Phase velocity is the speed at which the phase of any one frequency component of a wave travels.

Q: How is phase velocity related to given phase of a wave?

A: Any given phase of the wave appears to travel at the phase velocity.

Q: Can phase velocity be calculated?

A: Yes, phase velocity can be calculated.

Q: In what terms is phase velocity given?

A: Phase velocity is given in terms of wavelength λ (lambda) and wave period T.

Q: What is wavelength?

A: Wavelength is the distance between two consecutive crests or troughs of a wave.

Q: What is wave period?

A: Wave period is the time it takes for a wave to complete one full cycle.

Q: Can phase velocity change with changes in wavelength and wave period?

A: Yes, phase velocity can change with changes in wavelength and wave period.

Phase velocity

Relationship with group velocity and dispersion

Examples

Structure-borne sound

Matter wave

Waveguide

Questions and Answers

Q: What is phase velocity?

Q: How is phase velocity related to given phase of a wave?

Q: Can phase velocity be calculated?

Q: In what terms is phase velocity given?

Q: What is wavelength?

Q: What is wave period?

Q: Can phase velocity change with changes in wavelength and wave period?

Search by letter