Permutation

In combinatorics, a permutation (from the Latin permutare 'to interchange') is an arrangement of objects in a certain order. Depending on whether some objects may occur more than once or not, one speaks of a permutation with repetition or a permutation without repetition. The number of permutations without repetition is given as a factorial, while the number of permutations with repetition is given by multinomial coefficients.

In group theory, a permutation without repetition is a bijective self-mapping of a usually finite set, usually using the first natural numbers as reference sets. The set of permutations of the first natural numbers, with the sequent execution as a link, forms the symmetric group of degree . The neutral element of this group represents the identical permutation, while the inverse element is the inverse permutation. The subgroups of the symmetric group are the permutation groups.

Important characteristics of permutations are their cycle type, their order and their sign. With the help of the error states of a permutation, a partial order can be defined on the set of permutations of fixed length. Using their inversion table, each permutation can also be assigned a unique number in a factorial-based number system. Important classes of permutations are cyclic, fixed point free, self-inverse and alternating permutations.

Permutations have many applications within and outside mathematics, for example in linear algebra (Leibniz formula), analysis (rearrangement of series), graph theory and game theory, cryptography (encryption methods), computer science (sorting methods) and quantum mechanics (Pauli principle).

All six permutations of three colored balls

Combinatorial basics

Problem

A permutation is an arrangement of objects in a particular order or a rearrangement of objects from a given order. Examples of permutations are:

An anagram is a permutation of the letters of a word, such as ENKEL and NELKE.
Shuffling the cards of a deck results in a (ideally) random permutation of the cards.
In volleyball, the change of position after conquering the right of serve is a cyclical permutation of the players.
Many sorting methods work with successive transpositions, i.e. permutations that swap exactly two objects.

If not all objects are selected in such an arrangement, one speaks of a variation instead of a permutation; if the order does not play a role in the selection, one speaks of a combination. In counting combinatorics, the question now arises as to the number of possible permutations. Here we distinguish the case in which all objects are different from the case in which some of the objects are identical.

Permutation without repetition

A permutation without repetition is an arrangement of objects, all of which are distinguishable. After there are placement possibilities for the first object, there are only n-1 possibilities for the second object, only possibilities for the third n-2 object, and so on until the last object, which has only one free space left. The number of possible permutations of objects is thus given by the factorial

$n!=n\cdot (n-1)\cdot (n-2)\cdot \ldots \cdot 1$

indicated.

For example, there are $4!=4\cdot 3\cdot 2\cdot 1=24$ possible arrangements of four different colored balls in a row.

Permutation with repetition

A permutation with repetition is an arrangement of objects, some of which are indistinguishable. If exactly objects are identical, then they are permutable in their places without resulting in a new order. In this way, exactly arrangements are the same. Thus, the number of permutations of objects of which are identical is given by the falling factorial

${\frac {n!}{k!}}=n\cdot (n-1)\cdot \ldots \cdot (k+1)=n^{\underline {n-k}}$

Given. If there are not only one, but groups with $k_{1},\ldots ,k_{s}$ identical objects each, then all these objects can be swapped in their places without resulting in new arrangements. If we also count the objects that occur only once with multiplicity , then $k_{1}+\ldots +k_{s}=n$ and the number of possible permutations is given by the multinomial coefficient

${\frac {n!}{k_{1}!\cdot \ldots \cdot k_{s}!}}={\binom {n}{k_{1},\ldots ,k_{s}}}$

specify.

For example, there are ${\tfrac {4!}{2!\,1!\,1!}}={\tfrac {24}{2}}=12$ possible arrangements of four colored balls in a row if exactly two of the balls have the same color, and ${\tfrac {4!}{2!\,2!}}={\tfrac {24}{4}}=6$ possible arrangements when each two balls are of the same color.

Algorithms

A number of algorithms exist for the systematic generation of all permutations of n elements, which can often be well formulated recursively. These include, among others, the Steinhaus-Johnson-Trotter algorithm and the heap algorithm.

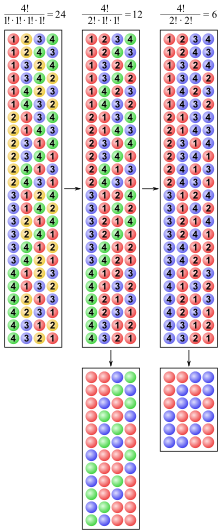
Permutations of four colored spheres without repetition (left) and with repetition (middle and right).

Definition

Let $X=\{x_{1},x_{2},\ldots ,x_{n}\}$ be a set with elements, then an -digit permutation (without repetition) is a bijective mapping

$\pi \colon X\rightarrow X$ ,

which assigns to each element of the set an element of the same set. Clearly, by permutation, each element $x_{i}$ for $i=1,\ldots ,n$ takes the place of its associated element π $\pi (x_{i})$ . Due to the bijectivity of the mapping, two different elements are never mapped to the same element in this case. The case n=0 is also allowed and is then the empty set.

Since, by definition, any finite set to a set of the form {1, 2, ..., n} is equipotent, one can always restrict the mathematical consideration of permutations to the first natural numbers as the reference set. A permutation is then a bijective mapping

$\pi \colon \{1,2,\ldots ,n\}\rightarrow \{1,2,\ldots ,n\}$ ,

which assigns to each natural number between and exactly one number in the same range. If we imagine all numbers lined up in a list, then the number takes the place with the number π $\pi (j)$ $j\in \{1,\ldots ,n\}$ by permutation.