Periodic function

This article deals with the mathematical term period in the meaning of the interval in the regular recurrence of a function value. See Period (decimal fraction) and Period for other meanings of the term.

In mathematics, periodic functions are a special class of functions. They have the property that their function values repeat at regular intervals. The intervals between the occurrence of the same function values are called period. Simple examples are sine and cosine functions. So that functions with gaps in the definition range, such as the tangent function, can also be counted as periodic functions, one allows definition ranges with periodic gaps. However, a periodic function does not have only one period, because each multiple of a period is also a period. Example: The sine function is not only $2\pi$ -periodic, but also $4\pi$ -periodic, ... When one speaks of period, one usually means the smallest possible positive period. However, there are periodic functions that do not have a smallest period. Example: any constant function defined on $\mathbb {R}$ has any number as its period.

Periodic functions occur naturally in physics to describe mechanical, electrical, or acoustic oscillatory processes. Therefore, a period is often denoted by (engl. : Time).

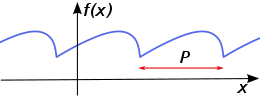
Since a periodic function is known if its course within a period is known, non-trigonometric periodic functions are usually defined in a basic interval and then continued periodically.

Just as many real functions can be developed in power series, one can, under certain conditions, develop a periodic function as a series of sine and cosine functions: see Fourier series.

Periodic sequences can be understood as special cases of periodic functions.

Functions that are not periodic are sometimes referred to - for extra emphasis - as aperiodic.

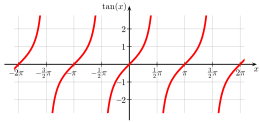
function graph of the tangent function

Illustration of a periodic function with period

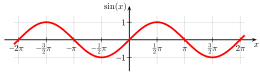
Function graph of the sine function

Real periodic functions

Definition

A real number is a period of a function defined in $\mathcal{D}_f \subseteq \mathbb{R}$ defined if for each from ${\mathcal {D}}_{f}$ holds:

$x+T$ is in ${\mathcal {D}}_{f}$ and
$f(x+T)=f(x)\;.$

The function is periodic if it $T \neq 0$ admits at least one period One then also says that is " -periodic".

For ${\mathcal {D}}_{f}=\mathbb {R}$ , which is often the case, the first property is always satisfied.

Properties of the periods

The following properties apply to the period:

If a period of then also a period of ;
If $T_{1}$ and $T_{2}$ two periods of , then $k_{1}T_{1}+k_{2}T_{2}$ with $k_{1},k_{2}\in \mathbb {Z}$ a period of .

Mostly one is interested in the smallest positive period. This exists for any nonconstant continuous periodic function. (A constant function is periodic with any period other than 0.) If has a least positive period, then the periods of are the multiples of . In the other case, the set of periods of is dense in $\mathbb {R}$ .

Examples

Trigonometric functions

The standard examples of periodic functions are the trigonometric functions. For example, the sine function defined on all of $\mathbb {R}$ defined sine function is periodic. Its function values repeat at intervals of $2\pi$ ( $\pi$ is the circular number Pi); thus, it has period $2\pi$ .
The tangent function with domain of definition $\mathbb {R} \setminus \{k\pi +{\tfrac {\pi }{2}}\;|\;k\in \mathbb {Z} \}$ is also a trigonometric function; it has period $\pi$ rather than $2\pi$ although it can be represented as the quotient of two $2\pi$ -periodic functions: $\tan x={\tfrac {\sin x}{\cos x}}$ .

Sum of cos and sin functions

Sums of cos and sin functions with a common (not necessarily smallest) period are again periodic. (In the figure, the common period is $2\pi$ .) This property of cos and sin functions is the basis of Fourier series. If two functions do not have a common period, the sum is not periodic. Example: $f(x)=\sin x+\sin(\pi x)$ is not periodic.

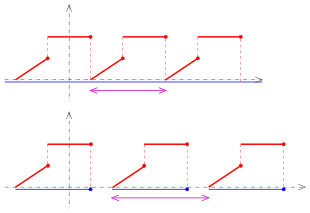
Periodic continuation

In the definition example at the top of the figure, a function given on a half-open interval (a,b] given on a half-open interval has been b-a $T=b-a$ continued to a periodic function of period by simply shifting by integer multiples of This type is called direct periodic continuation, to distinguish even and odd periodic continuation.

The following formal definition also provides a way to evaluate a periodically continued function with a computer, since the rounding function used is directly or indirectly realized in many mathematics systems.

DefinitionIf
a function $f_{0}$ on the interval [a, b] with $f_{0}(a)=f_{0}(b)$ is given, then the function with

$f(x)=f_{0}{\big (}x-\left\lfloor {\frac {x-a}{T}}\right\rfloor \cdot T{\big )},\;x\in \mathbb {R}$

the (direct) periodic continuation of $f_{0}$ on all of $\mathbb {R}$ and $\;T=b-a\;$ its period.
⌊ $\lfloor \cdot \rfloor$ is the rounding function. Using the rounding function ensures that the function is $f_{0}$ only evaluated for x values from its definition range (see figure).

Example: periodic continuation of parabolic arc $f_{0}(x)=(x-1)(4-x),\;a=1,b=4$ with period $\;T=b-a=3\;$ . The function value at the point (for example) $x=8$

$f(8)=f_{0}{\big (}8-\lfloor {\frac {7}{3}}\rfloor \cdot 3{\big )}=f_{0}(8-2\cdot 3)=f_{0}(2)=2\;.$

Since periodic functions are often developed in Fourier series and an even/odd periodic function can only be represented with cosine/sine terms, the following continuations are of particular interest:

Odd continuation:
In this case, one starts from a function $[0,b]$ defined on
the interval $f_{0}$ with $f_{0}(0)=f_{0}(b)=0$ . In a first step, one continues the function by mirroring it at the zero point on the interval : $[-b,0]$

$f_{u}(x)={\begin{cases}\quad f_{0}(x)\;,\ \quad 0\leq x\leq b\\-f_{0}(-x)\;,\;-b\leq x<0\ .\end{cases}}$

The function [-b,b] defined on the interval $f_{u}$ is now directly periodically continued (as described above). This gives rise to an odd periodic function defined on $\mathbb {R}$ defined odd periodic function of period $T=2b$ .

Just continued:
The analog procedure with

$f_{g}(x)={\begin{cases}f_{0}(x),\quad \ \ 0\leq x\leq b\\f_{0}(-x),\;-b\leq x<0\end{cases}}$

yields an even periodic function of period $T=2b$ .

Fourier series: Example

→ Main article: Fourier series

The Fourier series of a $2\pi$ -periodic odd function has the form

$\;\sum _{k=1}^{\infty }b_{k}\sin \left(kt\right)\;$

with

$b_{k}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(t)\cdot \sin \left(kt\right)\mathrm {d} t\quad {\text{für }}k\geq 1\;.$

The goal of a Fourier series expansion is to approximate a periodic function on (all of !) $\mathbb {R}$ by sums of simple periodic functions. Ideally, the Fourier series represents the given function on $\mathbb {R}$ . (A power series expansion approximates a function, which is not a polynomial, with its partial sums on a bounded (!) interval by polynomials).

In the figure, a function $[0,\pi ]$ given on the interval $f_{0}$ (two straight line segments, red) continued odd to a $2\pi$ -periodic function and then developed into a Fourier series (with sin terms only). One can see how well/badly partial sums of the Fourier series (of lengths n= 3,6,12) $f_{0}$ approximate the function While $f_{0}$ is discontinuous (it has jump points), the partial sums as sums of sin terms are all continuous.

In the example

$f_{0}(x)={\begin{cases}x\;,\ \quad 0\leq x\leq {\frac {\pi }{2}}\\2.5\;,\;{\frac {\pi }{2}}<x<\pi \\0\;,\qquad x=\pi \ .\end{cases}}$

and the partial sum for n=3:

$\;\sum _{k=1}^{3}b_{k}\sin \left(kt\right)={\frac {1}{\pi }}{\big (}7\sin x+({\frac {\pi }{2}}-5)\sin 2x+{\frac {13}{9}}\sin 3x{\big )}\ .$

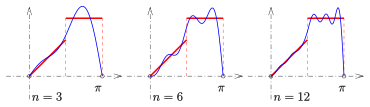
Fourier series: various Partial sums (blue)

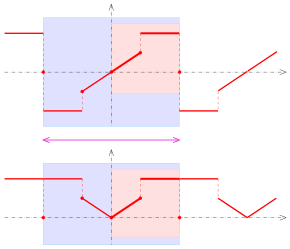
Periodic continuation of the function in the pink area: top: odd, bottom: even

Periodic function
above: ${\mathcal {D}}_{f}=\mathbb {R}$ . (blue),
bottom: ${\mathcal {D}}_{f}$ subset of $\mathbb {R}$ (blue),
purple: period

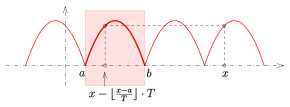
Periodic continuation of a parabolic arc

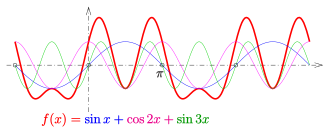
Sum of cos and sin functions

More general definition

The notion of periodic function is not limited to real functions. It can be defined more generally for functions on whose source set an addition is declared.

Let be an (additive) semigroup, a set, and $f\colon G\to M$ a function. If there exists a $T\in G$ with