Percentile

This article deals with quantiles of samples. For quantiles of probability distributions or random variables, see Quantile (probability theory).

An empirical ( p-)quantile, also called simply quantile for short, is a ratio of a sample in statistics. For any number pbetween 0 and 1, an empirical pdivides the sample such that a proportion of the sample of psmaller than the empirical pand a proportion of 1-pthe sample is larger than the empirical pquantile. For example, given a sample of shoe sizes, the empirical 0.35 quantile is that shoe size s such that 35% of the shoe sizes in the sample s are smaller than and 65% s are larger than

Some empirical pquantiles have proper names. They include the median ( p=0{,}5), the upper quartile and the lower quartile as well as the terciles, quintiles, deciles and percentiles.

Quantiles (in the sense of probability theory) are to be distinguished from the empirical quantiles discussed here. These are ratios of a probability distribution and thus of an abstract (quantity) function (similar to the expected value), whereas the empirical quantiles are ratios of a sample (similar to the arithmetic mean).

Definition

Let ⌊ {\displaystyle \lfloor x\rfloor }denote the rounding function. It rounds each number xto the nearest smaller integer. For example, ⌊ {\displaystyle \lfloor 1{,}2\rfloor =1}and ⌊ {\displaystyle \lfloor 3{,}99\rfloor =3}.

Given a sample {\displaystyle \left(x_{1},x_{2},\dotsc ,x_{n}\right)}size n, whose elements are ordered by size. This means that

{\displaystyle x_{1}\leq x_{2}\leq \dotsb \leq x_{n}}.

Then, for a number {\displaystyle p\in (0,1)}

{\displaystyle x_{p}={\begin{cases}{\tfrac {1}{2}}(x_{n\cdot p}+x_{n\cdot p+1}),&{\text{wenn }}n\cdot p{\text{ ganzzahlig,}}\\x_{\lfloor n\cdot p+1\rfloor },&{\text{wenn }}n\cdot p{\text{ nicht ganzzahlig.}}\end{cases}}}

the empirical p-quantile of {\displaystyle x_{1},x_{2},\dotsc ,x_{n}}.

Some definitions exist that differ from the definition given here.

Example

The following sample consists of ten random integers (drawn from the numbers between zero and one hundred, fitted with the discrete uniform distribution):

{\displaystyle 82;91;12;92;63;9;28;55;96;97}

Sort provides the sample

{\displaystyle x_{1}=9;x_{2}=12;x_{3}=28;x_{4}=55;x_{5}=63;x_{6}=82;x_{7}=91;x_{8}=92;x_{9}=96;x_{10}=97}.

It is {\displaystyle n=10}.

For p=0{,}5we get {\displaystyle p\cdot n=5}. Since this is an integer, we obtain via the definition

{\displaystyle x_{0{,}5}={\tfrac {1}{2}}\left(x_{5}+x_{5+1}\right)={\tfrac {1}{2}}(63+82)=72{,}5}

For {\displaystyle p=0{,}25}we get {\displaystyle p\cdot n+1=0{,}25\cdot 10+1=2{,}5+1}. The rounding function then yields ⌊ {\displaystyle \lfloor 3{,}5\rfloor =3}and thus

{\displaystyle x_{0{,}25}=x_{3}=28}.

Similarly, for {\displaystyle p=0{,}75}directly obtain {\displaystyle p\cdot n+1=0{,}75\cdot 10+1=8{,}5}and thus ⌊ {\displaystyle \lfloor 8{,}5\rfloor =8}, so

{\displaystyle x_{0{,}75}=x_{8}=92}.

In contrast to the arithmetic mean, the empirical quantile is robust to outliers. This means that if values of a sample above (or below) a certain quantile are replaced by a value above (or below) the quantile, the quantile itself does not change. This is based on the fact that quantiles are determined only by their order and thus their position with respect to each other, and not by the concrete numerical values of the sample. Thus, in the case of the sample above, the arithmetic mean would be {\displaystyle {\overline {x}}=62{,}2}. However, if we now modify the largest value of the sample, we set for example

{\displaystyle x_{10}=1000},

so {\displaystyle {\overline {x}}=152{,}8}, whereas the median, lower quartile, and upper quartile remain unchanged because the order of the sample has not changed.

Special quantiles

For certain pvalues, the associated quantiles have proper names. They are briefly introduced in the following. It should be noted that the corresponding quantiles of probability distributions are also partly designated with the same proper names.

Median

→ Main article: Median

The median is the {\displaystyle 0{,}5}quantile and thus divides the sample into two halves: one half is smaller than the median, the other larger than the median. Together with the mode and the arithmetic mean, it is an important location parameter in descriptive statistics.

Terzil

The two p-quantiles for {\displaystyle p={\tfrac {1}{3}}}and {\displaystyle p={\tfrac {2}{3}}}called terciles. They divide the sample into three equal parts: one part is smaller than the lower tercile (= {\tfrac {\displaystyle {\tfrac {1}{3}}}-quantile), one part is larger than the upper tercile (= {\displaystyle {\tfrac {2}{3}}}-quantile), and one part lies between the terciles.

Quartile

The two quantiles with {\displaystyle p=0{,}25}and {\displaystyle p=0{,}75}called quartiles. Here, the {\displaystyle 0{,}25}quantile is called the lower quartile and the {\displaystyle 0{,}75}quantile is called the upper quartile. Half of the sample lies between the upper and lower quartiles, and a quarter of the sample lies below the lower quartile and above the upper quartile, respectively. The interquartile range, a measure of dispersion, is defined on the basis of the quartiles.

Quintile

Quintiles are the four quantiles with {\displaystyle p=0{,}2;0{,}4;0{,}6;0{,}8}Accordingly, 20% of the sample is below the first quintile and 80% above it, 40% of the sample is below the second quintile and 60% above it, and so on.

Decile

The quantiles for multiples of {\displaystyle 0{,}1}, i.e. for {\displaystyle p=0{,}1;0{,}2;\dotsc ;0{,}9}are called deciles. Here, the {\displaystyle 0{,}1}quantile is called the first decile, the {\displaystyle 0{,}2}quantile is called the second decile, etc. Below the first decile are 10% of the sample, above correspondingly 90% of the sample. Similarly, 40% of the sample lies below the fourth decile and 60% above.

Percentile

Percentiles are the quantiles from {\displaystyle 0{,}01}to {\displaystyle 0{,}99}in steps of {\displaystyle 0{,}01}.

Derived terms

From the quantiles, certain measures of dispersion can be derived. The most important is the interquartile range.

{\displaystyle {\text{IQR}}:=x_{0{,}75}-x_{0{,}25}}.

It indicates how far apart the upper and lower quartiles are and thus how wide the range is in which the middle 50% of the sample lies. Somewhat more generally, the (inter)quantile distance can be defined as {\displaystyle x_{1-p}-x_{p}}for {\displaystyle p\in (0;0{,}5)}. It indicates how wide is the range in which the mean {\displaystyle 200\cdot p\,\%}the sample lies. For {\displaystyle p=0{,}25}it corresponds to the interquartile range.

Another derived measure of dispersion is the mean absolute deviation from the median.

View

One way of displaying quantiles is the box plot. Here, the entire sample is represented by a box - provided with two antennas. The outer boundaries of the box are the upper and lower quartiles. Thus, half of the sample is in the box. The box itself is subdivided again, the subdividing line is the median of the sample. The antennas are not uniformly defined. One possibility is to choose the first and the ninth decile as the limits of the antennas.

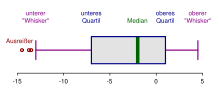
Box plot of a sampleZoom
Box plot of a sample


AlegsaOnline.com - 2020 / 2023 - License CC3