Pascal's triangle

Pascal's (or Pascal's) triangle is a form of graphical representation of binomial coefficients ${\tbinom {n}{k}}$ , which also allows a simple calculation of them. They are arranged in the triangle such that each entry is the sum of the two entries above it. This fact is explained by the equation

$\binom{n+1}{k+1} = \binom{n}{k} + \binom{n}{k+1}$

can be described. The variable can be interpreted as a row index and as a column index, where the count starts with zero (i.e. first row n=0 , first column k=0 ). If one starts at the edges with entries with the value this results in exactly the binomial coefficients.

The name goes back to Blaise Pascal. However, Pascal's triangle was known earlier and is therefore still named after other mathematicians. In China one speaks of the Yang-Hui triangle (after Yang Hui), in Italy of the Tartaglia triangle (after Nicolo Tartaglia) and in Iran of the Chayyām triangle (after Omar Chayyām).

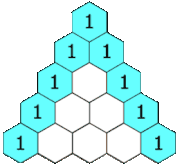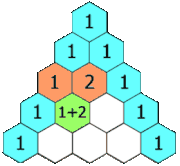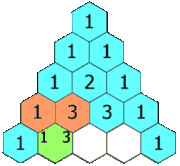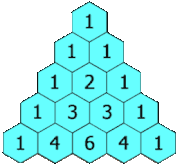
Each entry is the sum of the two entries above it.

History

The earliest detailed account of a triangle of binomial coefficients appeared in the 10th century in commentaries on the Chandas Shastra, an Indian book on Sanskrit prosody written by Pingala between the fifth and second centuries BCE. While Pingala's work survives only in fragments, the commentator Halayudha used the triangle around 975 to establish dubious relationships with Meru-prastaara the "steps of Mount Meru." It was also already known that the sum of the flat diagonals of the triangle gives the Fibonacci numbers. From the Indian mathematician Bhattotpala (approx. 1070) the first 17 lines of the triangle are handed down.

At about the same time, Pascal's triangle was treated in the Middle East by al-Karaji (953-1029), as-Samaw'al, and Omar Chayyām, and is therefore known in modern Iran as the Chayyām triangle. Various mathematical theorems concerning the triangle were known, including the binomial theorem. In fact, it is fairly certain that Chayyām used a method to calculate the -th root based on the binomial expansion and thus the binomial coefficients.

The earliest Chinese representation of an arithmetic triangle identical to Pascal's triangle is found in Yang Hui's book Xiangjie Jiuzhang Suanfa of 1261, excerpts of which are preserved in the Yongle Encyclopedia. In it, Yang writes of having adopted the triangle from Jia Xian (c. 1050) and his method of calculating square and cube roots called li cheng shi shuo ("determining coefficients by means of diagram").

Peter Apian published the triangle in 1531/32 on the cover of his book on trade calculations, whose earlier version of 1527 is the first written record of Pascal's triangle in Europe.

In 1655, Blaise Pascal wrote the book "Traité du triangle arithmétique" (Treatise on the arithmetic triangle), in which he collected various results concerning the triangle and used them to solve problems in probability theory. The triangle was later named after Pascal by Pierre Rémond de Montmort (1708) and Abraham de Moivre (1730).

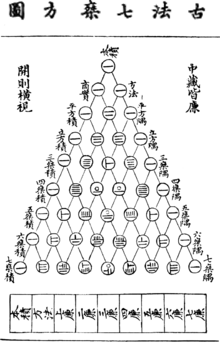
Yang-Hui triangle as described in a book written by Zhu Shijie in 1303.

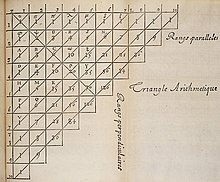
Blaise Pascal's version of the right triangle

Application

Pascal's triangle gives a handle to quickly multiply out arbitrary powers of binomials. For example, the second line ( n=2 ) contains the coefficients 1, 2, 1 of the first two binomial formulas:

$(a\pm b)^{2}=a^{2}\ \pm \ 2\cdot ab\ +\ b^{2}.$

In the next, the third line, we find the coefficients 1, 3, 3, 1 for $(a \pm b)^3$ :

$(a\pm b)^{3}=a^{3}\ \pm \ 3\cdot a^{2}b^{1}\ +\ 3\cdot a^{1}b^{2}\ \pm \ b^{3}.$

This list can be continued arbitrarily, whereby it is to be noted that for the binomial (a - b) always the minus sign from " $\pm$ " is to be taken and that, while the exponent of in each formula always decreases by 1, the exponent of increases by 1. A generalization is provided by the binomial theorem.

Furthermore, when Pascal's triangle is applied to the binomial $(a^{2}-b^{2})$ with any exponent, the signs - and + alternate (there is always a minus if the exponent of odd). This means, for example

$(a-b)^{4}=a^{4}\ -\ 4\cdot a^{3}b^{1}\ +\ 6\cdot a^{2}b^{2}\ -\ 4\cdot a^{1}b^{3}\ +\ b^{4}.$

A two-dimensional generalization is the Trinomial Triangle, in which each number is the sum of three (instead of two in Pascal's Triangle) entries. An extension into the third dimension is the Pascal's Pyramid.

Sequences in Pascal's triangle

In Pascal's triangle many well-known number sequences can be found.

The diagonals

The first diagonal contains only ones and the second diagonal contains the sequence of natural numbers. The third diagonal contains the triangular numbers and the fourth diagonal contains the tetrahedral numbers. In general, in the -th diagonal one finds the regular figured numbers of order . In each diagonal is the sequence of partial sums to the sequence that is in the diagonal above. Conversely, each diagonal sequence is the difference sequence to the sequence below in the diagonal.

In general, the following applies to the triangular numbers

$\Delta(n) = \binom{n+1}{2}$ ,

for the tetrahedral numbers

$T(n) = \sum_{k=1}^{n}\Delta(k) = \binom{n+2}{3}$

and for the regular figured numbers of order

$R(r,n) = \sum_{k=1}^{n} R(r-1,k) = \binom{n+r-1}{r}$ .

The Fibonacci numbers

$\color{OliveGreen}1$

$\color{blue}1$

$\color{red}4$

$\color{OliveGreen}6$

$\color{blue}10$

$\color{red}10$

$\color{OliveGreen}5$

$\color{blue}15$

$\color{red}6$

$\color{OliveGreen}1$

$\color{blue}7$

$\color{red}1$

$\color{blue}1$

126

120

210

252

210

120

The sums of the flat "diagonals" marked here in green, red and blue each give a Fibonacci number (1, 1, 2, 3, 5, 8, 13, 21, 34, ...). In this example, the sum of the green diagonal is equal to 13, the sum of the red diagonal is equal to 21, the sum of the blue diagonal is equal to 34. The fact that sometimes the "diagonal" cannot be "pulled through" from one end to the other, as in the case of the red diagonal, is irrelevant.

In general

$F(n)=\sum_{k=0}^{\lfloor \frac{n}{2} \rfloor} \binom {n-k-1}{k} = \sum_{k=0}^{\lfloor \frac{n}{2} \rfloor} \binom {n-k-1}{n-2k-1}, n \geq 1$

The lines

The sum of the entries in a row is called the row total. From top to bottom, the row sums double from row to row. This comes from the formation law of the Pascal triangle. Each entry of a line is used in the following line to calculate two entries. Here, one must generalize the formation law by adding imaginary zeros to the left and right of each line, so that the outer ones of each line are also generated by adding the entries above it. Since the row sum of the first row is equal to one, the row sum of the -th row is equal to $2^{n-1}$ . This corresponds to the following law for binomial coefficients:

$\sum_{k=0}^n \binom nk = \binom n0 + \binom n1 + \dotsb + \binom nn = 2^n$

If you line up the digits of the first five lines of the Pascal triangle, you get 1, 11, 121, 1331 and 14641, which are the first powers of 11.

The alternating sum of each line is zero: $\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}=0$ ,

Formally, the three formulas above follow from the binomial theorem $(1+x)^n = \sum_{k=0}^n \binom{n}{k} x^k$ for x=1 , x=10 and x=-1 .

Mean binomial coefficients

The sequence of mean binomial coefficients starts with 1, 2, 6, 20, 70, 252, ... (sequence A000984 in OEIS).

Alternative representation: The Fibonacci numbers as the sum of the diagonals (red lines).

Connection with the Sierpinski triangle

Pascal's triangle is related to Sierpinski's triangle, named in 1915 after the Polish mathematician Wacław Sierpiński. Both triangles use a simple but slightly different iteration rule that produces a geometric similarity.

Powers with arbitrary base

For powers with arbitrary base there exists a number triangle of a different kind:

$\begin{matrix} _i\backslash^j & {n \choose 1} & {n \choose 2} & {n \choose 3} & {n \choose 4} & {n\choose 5} \\ n^1 & 1 & & & & \\ n^2 & 1 & 2 & & & \\ n^3 & 1 & 6 & 6 & & \\ n^4 & 1 & 14 & 36 & 24 & \\ n^5 & 1 & 30 & 150 & 240 & 120 \end{matrix}$

This triangular matrix is arrived at by inversion of the matrix of coefficients of those terms representing the combinations without repetition of the form $\begin{pmatrix}n \\ k \end{pmatrix}$ for and so on. $k = 1, 2, 3, \dots$

Example

$\begin{pmatrix}n \\ 2 \end{pmatrix} = \frac{n\,(n-1)}{2} = - 0{,}5\, n + 0{,}5\,n^2$ .

Reading

$n^5 = 1\,\begin{pmatrix} n\\1 \end{pmatrix} + 30\,\begin{pmatrix} n\\2 \end{pmatrix} + 150\,\begin{pmatrix} n\\3 \end{pmatrix} + 240\,\begin{pmatrix} n\\4 \end{pmatrix} + 120\,\begin{pmatrix} n\\5 \end{pmatrix}$

Example

$6^5 = 1\cdot 6 + 30\cdot 15 + 150\cdot 20 + 240\cdot 15 + 120\cdot 6 = 7\,776$

The formation law of the coefficients for the coefficient in row and column is:

$E(i,j) = [ E(i-1,j-1) + E(i-1,j) ]\cdot j$

therefore E(i,j) = j! S(i,j) with the Stirling number S(i,j) .

With the help of this triangle one gains immediate insight into the divisibility of powers. Thus, any prime power n^p for is p>3 n {\displaystyle n} 6 p {\displaystyle This is essentially the content of Fermat's little theorem; but in addition it is shown that the expression a^p - a for all given not only by but for p>3 6. The greatest common divisor of the matrix coefficients starting with the second coefficient of the prime exponents for always corresponds to the denominator of the respective Bernoullian number (example: p=3 : denominator = 6; p=5 : denominator = 30 etc.)

With this number triangle, for example, it can be easily proved that $\forall n \in \mathbb{N}: n^5 - n^3$ is divisible by 24:

$0\cdot a+ 24\cdot b + 144\cdot c + 240\cdot d + 120\cdot e$ (where $a = \begin{pmatrix} n \\ 1 \end{pmatrix}$ , $b = \begin{pmatrix} n \\ 2\end{pmatrix}$ , etc.)

is always divisible by 24, since because of $n \in \mathbb{N}$ also $a,b,c,d,e \in \mathbb{N}$ are.

Connection with the Wallis product

In 1655, John Wallis used a checkerboard interpolation between the number sequences figured (per dimension) to compute for the first time a representation of 4/ $\pi$ as an infinite product.

Other

About the numbers with which a number occurs in Pascal's triangle there is the Singmaster conjecture.