Pareto efficiency
![]()
This article deals with the Pareto-optimal state. For the mathematical solution of the optimisation problem, see Pareto optimisation.
A Pareto optimum (also Pareto efficient state) is a (best possible) state in which it is not possible to improve one (target) property without having to worsen another at the same time.
The Pareto optimum is named after the economist and sociologist Vilfredo Pareto (1848-1923).
The set of all Pareto optima is also called the Pareto set (also Pareto front). The Pareto criterion is the assessment of whether a state improves by changing one target value (Pareto superiority) without having to worsen even one other target value. Vilfredo Pareto originally did not refer to target values/properties/criteria (sometimes also called "characteristics"), but to individuals. In relation to individuals, a Pareto-optimal (Pareto-efficient) state denotes a state in which there is no possibility of making one individual better off without making another worse off at the same time.
Mathematically expressed, the 











Solving the problem of finding Pareto optima is called Pareto optimisation.
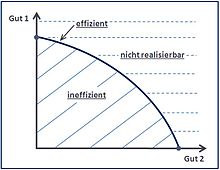
Pareto-efficient bundles of goods lie on the production possibility curve. No additional unit of either good can be produced if the production of the other good is not to be restricted.

Pareto optima (red) of a two-dimensional set of values (blue). Such a Pareto front does not have to be continuous - it can have interruptions.
Definition according to set theory
Let be 
















It should be noted that in the above definition only the existence of the natural numbers 
Examples
Example 1
A component should be both strong and light. It is therefore characterised by the two properties of strength and mass. The higher the strength and the lower the mass, the better the component. If one enters the pairs of values for many different components in a diagram that compares strength and lightness (reciprocal of mass), one obtains the quantity marked in blue in the adjacent diagram.
With the same mass, the component that is stronger is better. With the same strength, the component that is lighter is better. If the improvement of one value meets the deterioration of the other, the components are not Pareto-comparable.
In relation to the graph, values further to the right and further up are Pareto-superior to values to the left and below. All components on the red curve are "the best". They are Pareto-optimal. An increase of one value is then only possible if the other decreases. (On the red line, "further to the right" forces "further down"; conversely, "further up" forces "further left").
An additional condition or requirement can reduce the Pareto front to a single "(very) best" component (with respect to all three requirements). This can also be a standard that converts strength and mass into one quantity, thus making the points on the red line comparable, which leads to a clearly optimal solution (with regard to the standard). Depending on whether the quantities are comparable, it is sometimes not possible to find a standard.
Example 2
Assume that there are three individuals A, B and C living along a road. A well must be drilled to supply them with drinking water. Each individual must pay for the pipe from the well to his house. Therefore, each wants the well as close to his house as possible.
In the following sketch, the location of the three houses on the road is marked as A, B and C. In addition, the five possible locations for the well are marked as b1, b2, b3, b4 and b5. It is assumed that the vertical/horizontal distances to the nearest well or neighbour are 50 m each. Sketch of the possible locations for the fountain: (b1) (b2) (b3) (b4) (b5) =====|A|=====|B|=====|C|========Street =====
Set A = { b1, b2, b3, b4, b5 }
Parameters are the 3 tuple elements "Distance to A", "Distance to B" and "Distance to C":
- b1( 158.1 m, 150.0 m, 158.1 m )
- b2( 111.8 m, 100.0 m, 111.8 m )
- b3( 141.4 m, 111.8 m, 100.0 m )
- b4( 70.7 m, 50.0 m, 70.7 m )
- b5( 111.8 m, 70.7 m, 50.0 m )
For the first tuple element (= "distance to A") b4 is optimal, for the second tuple element b4 is also optimal, for the third tuple element b5 is optimal.
The Pareto optimum is therefore { b4, b5 }.
- The location b1 is not Pareto-optimal, because the location b2 is Pareto-superior to the location b1. Compared to b1, location b2 is an improvement for all parties involved.
- But even b2 is not Pareto-optimal, because b4 is Pareto-superior to b2. The location b4 is an improvement over b2 for all parties involved.
- The locations b2 and b3 are not comparable according to the Pareto criterion, since moving the well from b2 to b3 both makes one of the parties better off and makes another party worse off. The same applies to moving the well from b3 to b2. Weighing the advantages and disadvantages of different persons is not possible using the Pareto criterion.
- The location b3 is also not a Pareto optimum, because b5 is an improvement over b3 for everyone.
- The location b4 is Pareto-optimal, because there is no Pareto-superior alternative to b4 that makes (at least) one of the participants better off without at the same time making another worse off
- However, the location b5 is also Pareto-optimal, because any transfer of the well to one of the other locations would make Individual C worse off.
- The location b4 and b5 are not comparable according to the Pareto criterion, since a transfer of the well from b4 to b5 both makes one of the parties better off and makes another worse off. The same applies to a relocation from b5 to b4.

y-axis: strengthx-axis : "lightness" (=reasonable mass)
The Pareto criterion compared to the utility sum criterion
In economic theory, the criterion of Pareto optimality replaced the utilitarian criterion of the "sum of individual benefits" that had prevailed until then.
Under the influence of positivist philosophy of science, the notion of utility as a numerically (cardinally) measurable quantity that is comparable for different people (interpersonal) was not accepted.
Ordinal evaluations in the form of preferences (





The Pareto criterion in conjunction with a status quo regulation
Taken by itself, the Pareto criterion is a plausible and unproblematic criterion for social decisions. It advocates all changes that benefit anyone and harm no one.
However, it becomes ethically problematic if the optimality or efficiency defined in this way remains the only point of view.
As has been shown, there may be a multitude of Pareto optima that are not comparable with each other in terms of value. In economic reality, however, a selection takes place, because - as is usual with legal systems - the existing state, the status quo, remains if no decisions are made. Consequently, there is no change in the existing situation as long as only one owner suffers a disadvantage as a result. By combining the criterion of Pareto optimality with a status quo clause, the Pareto criterion works in favour of the existing conditions.
Use Case Economic Theory
A social situation is called economically efficient or Pareto-optimal if it is not possible to increase the welfare of one individual through a re-allocation of resources without simultaneously decreasing that of another individual. In other words, a condition where there is no way to make one individual better off without making another worse off at the same time. Since a Pareto optimum is a social optimum, such a state is always desirable. In contrast, a state is called Pareto-inefficient if there is another allocation that makes one individual better off without making another individual worse off.
Conditions for efficiency (Pareto optimality)
Pareto optimality of an economy means that the factors of production are allocated to an optimal use. This is the case when the following conditions are met:
1. exchange optimum
The marginal utility gains of all goods consumed by an individual are identical. One speaks of the marginal rates of substitution being equal (Gossen's second law). In this case, the individual consumes just those goods that maximise his utility.
2. optimal factor input
The marginal productivities of the factors used must be equal. This condition ensures that the largest possible quantity of goods is produced.
In modern economies, deviations from several conditions of Pareto optimality occur regularly. For example, monopolies, externalities, information asymmetries and the existence of public goods can simultaneously impair the functioning of the market mechanism. In this case, according to the theory of the second best, it is unclear whether an isolated measure to create the conditions has an efficiency-enhancing effect.
Criticism
The Pareto criterion is controversial in economics, especially in the context of social choice theory.
In an article published in 1970, Amartya Sen asserted the "impossibility of a Pareto liberal". Under assumptions similar to those Arrow had made for his famous impossibility theorem, but less stringent, he demonstrated that there are situations in which a "liberal mindset" (formalised as a social preference that strictly follows the preferences of the individual in question in certain situations) conflicts with the Pareto criterion. He illustrated this with an example in which a prudish person would like his neighbour not to read Lawrence's Lady Chatterley's Lover and would prefer to read the book himself, even if he dislikes it. The neighbour would like to read the book himself, but would prefer even more that the prude read it. Sen showed that, given the choice between the prude or no one reading the book, it would be libertarian-optimal to choose the latter, and given the choice between the libertine and no one, to choose the libertine, while it would be Pareto-optimal for the prude to read it. He concluded that the Pareto criterion should be questioned.
In practice, there will rarely be the possibility of government action or a change in the law that actually puts no one worse off. Guido Calabresi even argued that the criterion of Pareto optimality cannot be a guideline for the state because rational individuals will always have found Pareto-optimal solutions among themselves in private negotiations under the assumptions of the Coase theorem. State decisions would therefore necessarily always have a distributive effect; some of the citizens affected would always be worse off.
See also
- Kaldor-Hicks criterion
- Trade-off
Questions and Answers
Q: What is multi-criteria optimization?
A: Multi-criteria optimization is a way of solving a mathematical or economic problem where many different parameters need to be changed to get one of the best possible solutions to the problem.
Q: What is Pareto efficiency?
A: Pareto efficiency is the result of multi-criteria optimization named after Vilfredo Pareto. If there is no way of improving the situation of one person, without making that of another person worse, the solution found is Pareto-efficient.
Q: What is the Pareto frontier or Production Possibility Frontier?
A: The Pareto frontier or Production Possibility Frontier is where the economy is making (or "producing") all it can with the resources it has. Making more of one thing would mean making less of another.
Q: Does Pareto efficiency mean fairness or equity?
A: No, just because something is Pareto efficient, it doesn't mean it is fair or "equitable". It is possible that one person owns all of the world's things, and to make anyone else better off, some would have to be taken away from this person, making them worse off.
Q: Who first used the concept of Pareto efficiency in his studies?
A: Vilfredo Pareto first used the concept of Pareto efficiency in his studies.
Q: What is welfare economics?
A: Welfare economics is the study of how the allocation of resources affects economic well-being.
Q: What are some examples of resources or factors of production?
A: Some examples of resources or factors of production include machines, labour, land, and ideas.
Search within the encyclopedia