Skip to content
Home

Parallel postulate (Euclid's fifth postulate)

The parallel postulate: Euclid's fifth axiom that distinguishes Euclidean geometry. Covers its statement and equivalent forms, history of attempts to prove it, development of non‑Euclidean geometry, and consequences.

Author: Created: Updated:

The parallel postulate occupies a central place in the foundations of classical geometry. In Euclid's Elements it appears as the fifth axiom and is often called Euclid's fifth postulate. It is one of several basic assumptions in the study of geometry, explicitly singled out among Euclid's axioms that define Euclidean geometry. By contrast, non‑Euclidean geometry explores systems in which this postulate is altered or rejected.

Image gallery

3 Images
Elementorum 1747
en.wikipedia.org · CC BY 4.0

Statement and common formulations

Euclid's original wording describes two straight lines cut by a transversal: if the interior angles on one side sum to less than two right angles, the lines meet on that side when extended. A commonly used modern equivalent is Playfair's axiom: through a given point not on a line there is exactly one line parallel to the given line. Many other statements are logically equivalent to the parallel postulate within standard axiom systems; they express uniqueness of parallels, the angle sum of triangles, or behavior of similar figures.

Consequences and equivalent statements

  • Playfair's axiom (unique parallel through a point not on a line).
  • The angles of a triangle sum to two right angles (180°) in the plane.
  • Existence of similar triangles of different sizes underlies many Euclidean similarity results.
  • Parallel lines remain at a constant distance and never meet.

These equivalences mean that adopting any one of these statements in a standard axiomatic framework leads to all the others, and thus to the familiar properties of the Euclidean plane.

History and the rise of non‑Euclidean geometry

For two millennia geometers tried to derive the parallel postulate from Euclid's other axioms, considering it less self‑evident. Efforts by medieval and early modern mathematicians produced many alternative formulations and partial proofs, but none succeeded. In the 19th century mathematicians such as Lobachevsky, Bolyai and Riemann developed coherent geometries in which the parallel postulate does not hold. Later work by Beltrami, Klein and Poincaré constructed models showing that the negation of the postulate is consistent whenever Euclid's other axioms are, establishing its logical independence.

Importance and modern perspective

Today the parallel postulate is seen as a choice that determines the global geometry of a surface. Retaining it yields classical Euclidean geometry with familiar distance and angle relations; replacing it yields hyperbolic geometry (many parallels through a point) or elliptic geometry (no parallels). Modern axiom systems, for example Hilbert's, make the status of the parallel postulate explicit and allow rigorous comparison of different geometries. The study of these alternatives has deepened understanding of space, influenced the development of differential geometry and provided mathematical language used in physics, topology and other fields.

For further reading on foundations and historical context see general treatments of Euclidean geometry, discussions of non‑Euclidean geometry, Euclid's original Elements, biographies of Euclid, and general texts on axiomatic axioms and geometric foundations.

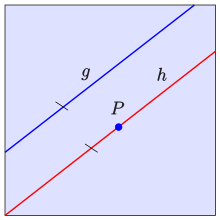
Parallel axiom
Parallel axiom
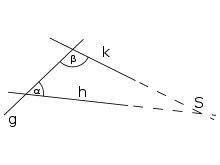
Intersection S of h and k if α+β<180°.
Intersection S of h and k if α+β<180°.

History

This postulate clearly stands out from the other postulates and axioms due to its length and complexity. It was perceived as a flaw (unsightly feature) in Euclid's theory even in ancient times. Again and again there were attempts to derive it from the others and thus to show that it was dispensable for the definition of Euclidean geometry. Historically, this task is known as the parallel problem and remained unsolved for over 2000 years. Unsuccessful attempts were made, for example, by

  • Archimedes (3rd century BC)
  • Poseidonius (2nd/1st century BC)
  • Ptolemy (2nd century)
  • Proclus (5th century)
  • Agapius (5th/6th century AD, disciple of Proclus), quoted by Al-Nayrizi
  • Simplikios
  • al-Abbas ibn Said al-Dschauhari
  • Thabit ibn Qurra (9th century)
  • Alhazen
  • Omar Chayyam
  • Nasir Al-din al-Tusi (13th century)
  • Giovanni Alfonso Borelli (17th century)
  • John Wallis (17th century)
  • Giovanni Girolamo Saccheri (18th century), see also Saccheri quadrangle
  • Johann Heinrich Lambert (18th century)
  • Adrien-Marie Legendre (18th/19th century)

Carl Friedrich Gauss was the first to recognise that the parallel problem is fundamentally unsolvable; however, he did not publish his findings. He did, however, correspond with various mathematicians who pursued similar ideas (Friedrich Ludwig Wachter, Franz Taurinus, Wolfgang Bolyai).

Equivalent formulations

A number of statements were also found that are equivalent to the Euclidean parallel postulate under the condition of the remaining axioms of plane Euclidean geometry. The underlying axioms are the plane incidence axioms (I.1 to I.3), the axioms of arrangement (group II), the axioms of congruence (group III) and the axioms of continuity (V.1 and V.2) in Hilbert's axiom system of Euclidean geometry:

  • "The sum of the angles in the triangle is two rights (180°)." (cf. Giovanni Girolamo Saccheri)
  • "There are rectangles."
  • "For every triangle there is a similar triangle of any size". (John Wallis).
  • "Step angles at parallels are equal".
  • "Through a point inside an angle there is always a straight line that intersects the two legs."
  • "Through three points not lying on a straight line there is a circle". (Farkas Wolfgang Bolyai)
  • "Three points that lie on one and the same side of a straight line and have congruent distances to this straight line always lie on a common straight line."

Non-Euclidean Geometry

In 1826, Nikolai Lobachevsky was the first to present a new type of geometry in which all the other axioms of Euclidean geometry apply, but not the parallel axiom, Lobachevskian or hyperbolic geometry. This proved that the parallel axiom could not be derived from the other axioms of Euclidean geometry.

János Bolyai independently arrived at similar results almost simultaneously.

This led to the development of non-Euclidean geometries, in which the postulate was either completely deleted or replaced by others. In some cases, non-Euclidean geometries also violate other axioms of Euclidean geometry besides the parallel axiom.

Elliptic parallel axiom

Thus, in an elliptical plane it is not possible for Hilbert's arrangement axioms (group II) and the congruence axioms for distances (III.1, III.2 and III.3) to be fulfilled at the same time. Here, in the sense of congruence, one can "sensibly" only introduce an arrangement ("separation relation" through four instead of three points in the case of a Hilbertian intermediate relation) as for projective planes, because elliptical planes in the sense of metric absolute geometry are also projective planes, their "elliptical" (actually projective) parallel axiom is simply: "There are no non-intersections, two different straight lines of the plane always intersect at exactly one point" see Elliptical Geometry#Marking.

The figure at the top right illustrates the difference between an arrangement on an affine straight line gat the top of the picture and a projective straight line represented by the circle hbottom of the picture. On an affine straight line ga Hilbert intermediate relation is definable if the coordinate range can be arranged. Every affinity that maps the (unordered) pair set \{G_{1},G_{2}\}onto itself also forms the "line" g_{1}which is the set of intermediate points of (G_{1},G_{2})onto itself. In fact, exactly four such affinities exist: Two of them (identity and perpendicular axis reflection on G_{1}G_{2}) hold the straight line as a whole, the other two, the perpendicular axis mirroring and the point mirroring at the (affine) line centre of (G_{1},G_{2})interchange the points G_{1},G_{2}and the half-straights g_{2},g_{3}.

The situation is different on an affine circle and a projective straight line. Two points divide the affine circle line into two arcs. Affinities of the plane that map \{H_{1},H_{2}\}and the circular line onto themselves also map the two arcs each onto themselves, unless H_{1},H_{2}lie on the same diameter, then h_{1}and h_{2}can also be exchanged by the point reflection at the centre of the circle and by the (perpendicular) axis reflection at the diameter H_{1}H_{2}.

The circle line can be understood as a model of a projective straight line over an arranged body Kprojecting it centrally from a point P=H_{\infty }this circle line onto the circle topposite the point. The point Pis thus tassigned to the far point of For a projective plane over Kthere exist for any two points T_{1},T_{2}\in twhich in the picture are associated with the points H_{1},H_{2}on the circular line, projectivities of the plane which map the point set \{T_{1},T_{2}\}onto themselves, but point sets t_{1},t_{2}\subset t, corresponding toh_{2} h_{1}and interchange with each other. In short: On an arranged projective straight line one cannot distinguish "inside" and "outside" projectively invariant!

Note that also in the case of the straight line gtop of the picture, if it is understood as a real, projective straight line, the complementary set c=g\setminus sthe closed affine line s=g_{1}\cup \{G_{1},G_{2}\}which then also gcontains the far point of is ga connected subset of respect to the order topology!

Hyperbolic parallel axiom according to Hilbert

In 1903 David Hilbert gave the following formulation for a parallel axiom of hyperbolic geometry, compare also the figure on the right:

If bany straight line and Apoint not on it, then there are always through Atwo half-straights a_{1},a_{2}which do not make up one and the same straight line and do bnot intersect the straight line while each half straight line located in the angle space (a_{1},a_{2})formed by \angle (a_{1},a_{2})Astarting from bintersects the straight line

The angle space \angle (a_{1},a_{2})is marked by an arc (light blue) in the figure on the right. All half-lines with starting point Awhich do not lie in this angle space do not intersect the straight line b.

In Hilbert's axiom system mentioned above, one can replace the Euclidean parallel axiom (IV by Hilbert) with Hilbert's hyperbolic parallel axiom. Thus one obtains (for the plane to which Hilbert restricts himself here, i.e. of the group of incidence axioms only I.1 to I.3 are needed) a contradiction-free axiom system for which there is exactly one model (except for isomorphism): The real, hyperbolic plane, which can be modelled, for example, by the (real) Klein circular disk model within the real Euclidean plane. He outlines the proof himself in his Fundamentals. A complete proof was given by Johannes Hjelmslev in 1907.

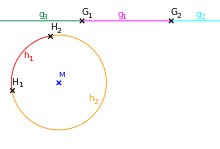
On the difference between affine and projective arrangement.
On the difference between affine and projective arrangement.
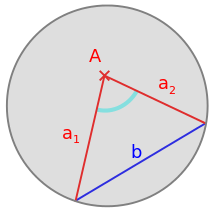
Hilbert's hyperbolic parallel axiom in Klein's circular disk model of (real) hyperbolic geometry. The formulation of Hilbert's axiom with half-straights presupposes an arrangement of the hyperbolic plane in the sense of Hilbert's axioms. Note that only the points inside the circle line (grey) are points of the hyperbolic plane.
Hilbert's hyperbolic parallel axiom in Klein's circular disk model of (real) hyperbolic geometry. The formulation of Hilbert's axiom with half-straights presupposes an arrangement of the hyperbolic plane in the sense of Hilbert's axioms. Note that only the points inside the circle line (grey) are points of the hyperbolic plane.

Questions and answers

Q: What is the parallel postulate in geometry?

A: The parallel postulate in geometry is one of the axioms of Euclidean geometry, stating that if you cut a line segment with two lines, and the two interior angles the lines form add up to less than 180°, then the two lines will eventually meet if you extend them long enough.

Q: Why is the parallel postulate sometimes called Euclid's fifth postulate?

A: The parallel postulate is sometimes called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements.

Q: What is the field of geometry that follows all of Euclid's axioms called?

A: The field of geometry that follows all of Euclid's axioms is called Euclidean geometry.

Q: What are geometries that do not follow all of Euclid's axioms called?

A: Geometries that do not follow all of Euclid's axioms are called non-Euclidean geometry.

Q: What happens if the two interior angles formed by two lines add up to more than 180°?

A: If the two interior angles formed by two lines add up to more than 180°, the two lines will never meet no matter how long they are extended.

Q: What is Euclidean geometry?

A: Euclidean geometry is the field of geometry that follows all of Euclid's axioms.

Q: What is non-Euclidean geometry?

A: Non-Euclidean geometry is the field of geometry that does not follow all of Euclid's axioms.

Related articles

Author

AlegsaOnline.com Parallel postulate (Euclid's fifth postulate)

URL: https://en.alegsaonline.com/art/74535

Share