Parabola

In mathematics, a parabola (via Latin parabola from ancient Greek παραβολή parabolḗ "juxtaposition, comparison, simile, equality"; traced back to παρά pará "next to" and βάλλειν bállein "to throw") is a second-order curve and is therefore describable via a second-degree algebraic equation. Along with the circle, the ellipse, and the hyperbola, it is one of the conic sections: it is formed when a straight circular cone intersects a plane that is parallel to a generatrix and does not pass through the apex of the cone. Because of this very special intersection requirement, the parabola plays a special role among the conic sections: it has only one focal point and all parabolas are similar to each other.

The parabola was discovered by Menaichmos and named parabolḗ by Apollonios of Perge (c. 262-190 BC).

Parabolas often appear in mathematics as graphs of quadratic functions . $x\mapsto f(x)=ax^{2}+bx+c$

Parables also play a role in daily life:

Parabola with focal point , vertex and directrix

Definition with guideline

A parabola can be described geometrically as a locus line:

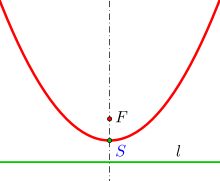
A parabola is the geometric locus of all points whose distance d(P,F) to a special fixed point - the focal point - is equal to the distance d(P,l) to a special straight line - the directrix .

Noted as a point set:

$\{P \mid d(P,F) = d(P,l)\}$

The point midway between the focal point and the directrix is called the vertex of the parabola. The line connecting the focal point and the vertex is also called the axis of the parabola. It is the only axis of symmetry of the parabola.

If one introduces coordinates in such a way that $F=(0,f)\ ,f>0$ and the directrix has the equation y=-f , then for P=(x,y) from $d(P,F)=d(P,l)$ results the equation

$y=\tfrac{1}{4f}x^2$

of a parabola open at the top.

The half-width of the parabola at the height of the focal point results from $y=f={\tfrac {1}{4f}}x^{2}$ to p=2f and is called (analogous to ellipse and hyperbola) the half-parameter of the parabola. As with ellipse (in the principal vertex) and hyperbola, the half-parameter p {\displaystyle p} is the vertex radius of curvature, that is, the radius of the circle of curvature at the vertex. In addition, for a parabola, the distance from the focal point to the directrix. The equation of the parabola can thus also be written in the following form:

x^2=2py

If we swap and , then one obtains with

y^2=2px

the equation of a parabola opened to the right.

Based on the definition, a parabola is the equidistance curve to its focal point and directrix.

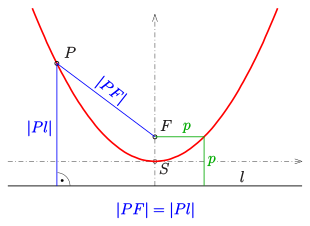
Parabola: Definition with focal point F, directrix l (black) and half-parameter p (green). The perpendicular Pl and the distance PF (each blue) are the same length for all points P of the parabola (red).

Parabola as function graph

An upward or downward open parabola with vertex at zero (0,0) and the axis as axis is described (in Cartesian coordinates) by an equation

$y=ax^{2}{\text{ mit }}a\neq 0$

described. For a>0 the parabolas are open upwards, for a<0 downwards (see figure). Thereby holds:

The focal point is $(0,{\tfrac {1}{4a}})$ ,
the half-parameter is $p=\tfrac{1}{2a}$ ,
the directrix has the equation $y=-{\tfrac {1}{4a}}$ and
the tangent line at the point has the equation $y=2ax_{0}x-ax_{0}^{2}$ .

For a=1 get the normal parabola y=x^2 . Its focal point is $(0,{\tfrac {1}{4}})$ , the half-parameter $p=\tfrac{1}{2}$ and the directrix has the equation $y=-{\tfrac {1}{4}}$ .