P versus NP problem

The P-NP problem (also P≟NP, P versus NP) is an unsolved problem in mathematics, specifically complexity theory in theoretical computer science. The question here is whether the set of all problems that can be solved quickly ( ) and the set of all problems for which one can quickly check a proposed solution for correctness ( ) are identical.

While it is clear that for all problems that can be solved quickly, one can also quickly check the correctness of a solution, this is not clear in the opposite direction: For some problems, an algorithm exists that can quickly check a proposed solution, but neither could an algorithm be found that also quickly finds a correct solution, nor could the impossibility of such an algorithm be proven. Thus, the problem is unsolved. If for all quickly testable problems an algorithm could be found that also solves them quickly, then . If it could be shown for at least one problem from that this problem is in principle not fast solvable, would be proved.

In this context, a problem is considered to be quickly solvable or a solution is considered to be quickly testable if an algorithm exists in which the increase in computational effort (number of computational steps) is limited by a polynomial function as the input becomes larger and this increase is not exponential. The size of the input here is, simply put, the number of elements that are input to the algorithm. In a problem such as sorting index cards, this would be the number of index cards.

History

The problem was recognized in the early 1970s due to independent work by Stephen Cook and Leonid Levin.

The P-NP problem is considered one of the most important unsolved problems in computer science and was included in the list of Millennium Problems by the Clay Mathematics Institute.

As became known later, a formulation of the problem can already be found in a letter by Kurt Gödel, which he sent to John von Neumann shortly before his death (on March 20, 1956). Another early formulation is found in a letter from John Forbes Nash to the National Security Agency in 1955, concerning cryptography.

P and NP

Complexity theory classifies problems that can be computed by computers according to the amount of time or memory required to solve them, or more precisely, according to how fast the effort grows with the size of the problem. For example, one problem is sorting index cards. It is now possible to examine how the time required changes when a stack twice as large is sorted.

The measure of computational effort used here is the number of computational steps required by the algorithm to solve a problem (time complexity). In order to specify the computational effort unambiguously, formal machine models are also required to represent the solution algorithms. A frequently used model is the deterministic Turing machine, which can be regarded as the abstraction of a real computer.

P

One of the problem categories is the complexity class . It contains the problems for which there exists a deterministic Turing machine that solves the problem in polynomial time. That is, there exists a polynomial with , so that for no problem instance (with length of the input) does the Turing machine need more computational steps than Problems from are thus deterministically solvable in polynomial time.

The above sorting problem is in P because there are algorithms that sorted a number of records (index cards) in a time bounded by a quadratic function in Another example of a problem in is the circuit evaluation problem.

The difference between a Turing machine and real computers does not matter here, because any algorithm that solves a problem in polynomial time on a real computer can also be implemented in polynomial time with a Turing machine (though the degree of the polynomial limiting the running time will usually be higher).

NP

Another machine model is the non-deterministic Turing machine (NTM), it is a generalization of the deterministic variant. An NTM can have several possibilities to continue its computation in a situation, so the computational path is not always uniquely determined. It is a theoretical model, there are no real-world computers that can branch their computational path in such a way. Its utility in this context is that it can be used to define another complexity class , which contains many problems of practical interest that are not yet known to lie in

is defined as the set of problems solvable by an NTM in polynomial time. The deterministic Turing machine is a special case of the NTM, it does not branch the computational path. Therefore, is a subset of .

One can define equivalently as the set of problems of which it is possible to decide in polynomial time using a deterministic Turing machine whether a proposed solution holds. For example, no deterministic algorithm is currently known to factorize a given number in polynomial time. However, it is very easy to test whether a proposed factor divides the number without a remainder and is therefore a factor of the number.

Is P=NP?

It is unknown whether the two classes and are identical, i.e., whether the hardest problems in the class are also efficiently solvable by deterministic machines. To formally capture the notion of "hardest problem in ", the notions of NP-completeness and NP-hardness were introduced. A problem X is NP-hard if one can reduce every problem in to X by polynomial-time reduction. Should one find an NP-hard problem X that can be solved deterministically in polynomial time, one could also solve any problem in deterministically polynomially by reducing it back to X, and it would be shown A problem that lies in and is NP-hard is called NP-complete.

An illustrative NP-complete problem is the knapsack problem: a container of a certain size is to be filled with a selection of given items in such a way that the contents are as valuable as possible without exceeding the capacity of the container. Another important example is the satisfiability problem in propositional logic.

It was also shown that if and thus the NP-complete problems are not in , then in there are also problems that are neither NP-complete nor in , that is, intermediate in difficulty. A candidate for such a problem is the graph isomorphism problem, which so far is not known to be in , nor to be NP-complete.

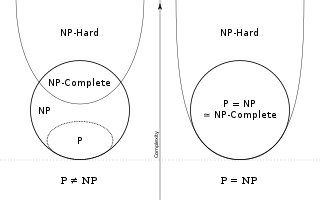
Relationship of problems in P and NP and of NP-severe and NP-complete


The complexity class NP, under the assumption P≠NP. In this case, NP also contains problems above P that are not NP-complete.