Oval
![]()
The title of this article is ambiguous. For other meanings, see Oval (disambiguation).
The term oval (Latin ovum 'egg') refers to a flat roundish convex figure, broadly resembling the profile of a bird's egg. It includes circles and ellipses as special cases, although unlike these, any oval need not have an axis of symmetry.
The use of the term is not always completely uniform, occasionally it is also used in a purely descriptive way. In analysis, however, it can be formally defined with the aid of plane curves, in which context it is also referred to as egg curves or rapid lines.
A three-dimensional round convex body (more generally also a closed convex subset of 
In projective geometry the notions of oval and ovoid are defined as quadratic sets without differentiability and convexity conditions exclusively by means of incidence conditions ("every straight line meets an oval or ovoid in at most 2 points"). An oval, as explained in the present article, is always an oval in the sense of the projective definition in the projective closure of the real plane, if one additionally requires that the curvature of the oval does not vanish on any section. Such an oval is then the boundary of a strictly convex set, i.e., it contains no straight line segments.
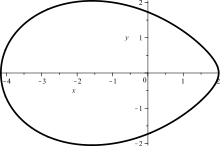
Oval with an axis of symmetry
Formal definition and properties
The roundish shape of an oval is obtained by requiring smoothness and convexity for a closed curve. This then leads to the following definition:
A closed twice continuously differentiable convex curve in the plane is called an oval (also egg curve or egg line).
However, this definition does not cover all geometric figures that are sometimes called ovals. For example, ovals composed of different circular arcs do not satisfy this definition, since their second derivative is not continuous on the entire curve. If one wishes to include such cases, one must make sacrifices to the smoothness of the curve (differentiation class 

An oval as defined above has the following properties:
- An oval is a Jordan curve, meaning it has no loops or loops.
- The oriented curvature of an oval has no change of sign, i.e., depending on the sense in which it passes, the oriented curvature for each point of the oval is either non-negative or non-positive. Graphically, this means that it has no turns or indentations. It can only be traversed in a pure left-hand curve or right-hand curve.
- The interior of an oval is a convex set, and the oval forms its boundary.
- For ovals, the Four-Point Theorem applies, which means that the curvature of an oval has at least four extreme points.
- If a point of the oval has a tangent, the entire oval is on one side of the tangent.
- If one additionally requires that the curvature of the oval does not disappear on any section, that is, the curvature assumes the value zero at most in isolated points, then the above tangent exists in every point of the oval. More generally, any straight line has either no point (passant), exactly one point (tangent) or exactly two points (secant) in common with the oval.
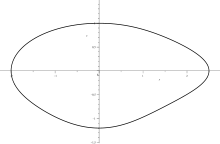
Oval without symmetry axes
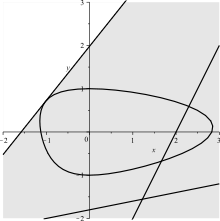
Oval with tangent, secant and passant
Examples and constructions
Ovals can be constructed using completely different methods. A number of construction methods are obtained from the various construction methods for ellipses, each of which is slightly modified at a suitable point.
One can create an ellipse by intersecting a cone with a plane (see conic sections). If one now uses certain other bodies of revolution instead of the cone, for example a rotated hyperbola, one also obtains ovals different from ellipses when intersecting with a plane. Another possibility is to use the constant parameters 



One can 




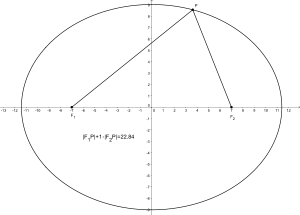
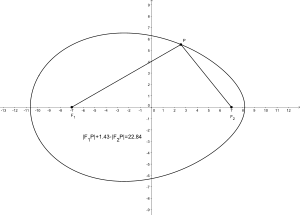
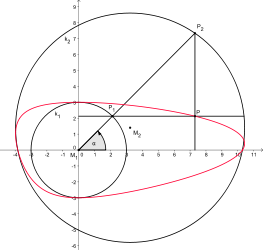
The construction method of de La Hire creates an ellipse with the help of two concentric circles. If you move the center of the outer circle a little bit and keep the remaining steps of the construction method, you get a (new) oval. This oval has an axis of symmetry if you move the center of the outer circle along the axes of the ellipse. If you move the center outside the axes, you get an oval without symmetry axes.
· 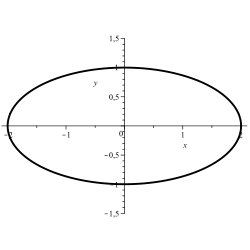
Ellipse:
· 
· 
Ellipse:
· 
· 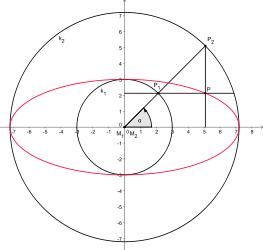
Construction with concentric circles
· 
Construction with eccentric circles
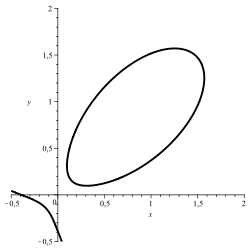
The solution set of an equation with two unknowns or certain subsets of it can often be understood as curves in the plane. If the equation is suitable, an oval is obtained. If such a solution curve is not an oval, but has a convex loop, an oval can be generated from the loop by adding a correction term.
· 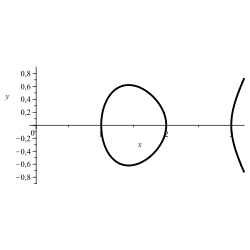
Elliptic curve:
· 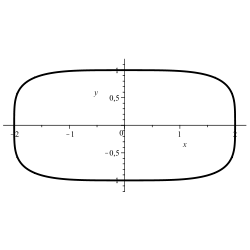
Lamé's oval:
· 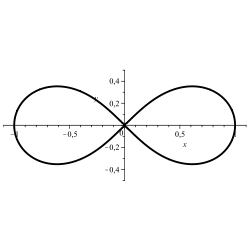
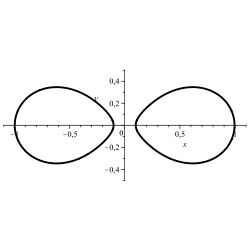
Lemniscate:
· 
Cassini curve:
· 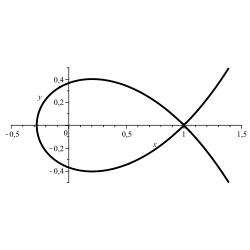
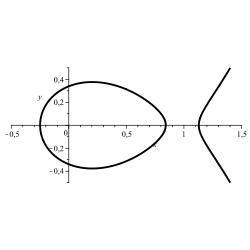
Szegö curve:
· 
· 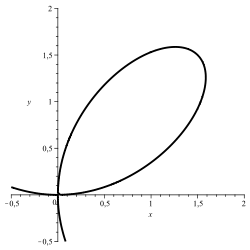
Cartesian sheet:
· 
Search within the encyclopedia












