Osmosis

This article is about the process of osmosis; for the French record label of the same name, see the article Osmose Productions.

Osmosis (ancient Greek ὠσμός ōsmós "penetration", "push", "thrust", "propulsion") is the term used in the natural sciences to describe the directed flow of particles through a selective or semipermeable interface. Osmosis is often described as the spontaneous passage of water or another solvent through a semipermeable membrane that is permeable to the solvent but not to the substances dissolved in it.

Osmosis is of central importance in nature, especially for the regulation of the water balance of living organisms and their cells. As a separation process, it finds application in medicine and process engineering, and it is used in osmotic power plants for energy generation. While osmosis is theoretically explained within the framework of statistical mechanics as well as non-equilibrium thermodynamics, the physical processes at the microscopic-molecular level are still the subject of scholarly dispute and active research activity at the beginning of the 21st century.

An illustrative example of the effect of osmosis is the bursting of ripe cherries after wetting with rainwater. The water on the outside of the fruit contains very few dissolved particles and therefore has a high chemical potential. It penetrates through the outer skin into the fruit, where the water as a solvent has a low chemical potential due to the high sugar content and other dissolved substances. The influx of water increases the pressure inside the fruit and causes its outer skin to tear. Among other substances, this skin is permeable to water, but not to sugar molecules; because of these properties, it acts as a semipermeable membrane. In principle, water molecules can pass through this membrane in both directions, but are more strongly "held" inside the fruit. There, the water molecules have to compete with the other dissolved molecules and particles for access to the membrane, so that fewer water molecules per unit time penetrate to the outside than vice versa.

The driving force of spontaneously occurring osmosis is the difference between the chemical potentials of one or more substances in the phases separated by a membrane. These can consist of liquid and gaseous solutions or pure substances. Particles (atoms, molecules or ions) of the components for which the membrane is permeable diffuse towards their lower chemical potential. The mixing process resulting from this movement reduces the Gibbs energy (or free enthalpy) of the overall system; therefore, the process proceeds without energy input (see also exergonic and endergonic reactions). In general, it is a solvent that diffuses towards its lower chemical potential due to the difference in the number of dissolved particles.

In closed systems, osmosis balances the potential differences; the osmotic movement continues until the chemical potential of the diffusing components on both sides of the membrane is balanced; a thermodynamic equilibrium has then been established between the two phases. If the substance flows into a closed volume, the pressure in this volume (the side with the initially lower potential) must inevitably increase; this difference is called the osmotic pressure. The osmotic pressure is a colligative property, since it depends on the number of dissolved particles.

Basics

In osmosis, a difference in concentration between the two sides can only be compensated for by the flow of substances that can pass through the membrane due to their properties. In many cases this is the solvent, e.g. water in biological systems.

As shown in the example on the right, water flows through the membrane from the side of lower concentration (in the figure the left half of the U-tube); its quantity decreases there and leads to a corresponding increase in volume on the other side. The movement of the solvent ends as soon as an equal chemical potential has been established on both sides of the membrane. In the figure, it is the hydrostatic pressure of the right liquid column that counteracts the further flow of solvent.

If, after reaching equilibrium, the water on one side is labelled with D2O (heavy water) or ^3H2O (superheavy water), it can be shown that an exchange of water molecules continues to take place. At equilibrium, however, the amount of molecules flowing in and out is the same on both sides.

Thermodynamic consideration

Spontaneous osmosis involves a mixing process - a substance passes from one phase into the other and mixes there with the components present. In closed systems, spontaneous mixing processes lead to a reduction in free enthalpy (Gibbs energy) and an increase in entropy. In the case of osmosis, the selectively permeable membrane acting as a barrier prevents all concentration differences from disappearing when thermodynamic equilibrium is reached; two separate phases are present at any given time. (In fact, three phases if the membrane is included in the consideration).

The total change in free enthalpy in the osmotic cell must therefore be written as the sum of the changes in both phases:

$\mathrm {d} G=\mathrm {d} G^{(1)}+\mathrm {d} G^{(2)}\$

where the superscript ^(x) denotes the respective section of the osmotic cell. If only one type of substance (e.g., the solvent) is allowed to pass through the membrane, the relationship between free enthalpy and change in the amount of substance can be $\mathrm {d} n_{L}$ given by

$\mathrm {d} G^{(1)}=\mu ^{(1)}\mathrm {d} n_{L}$ and $\mathrm {d} G^{(2)}=\mu ^{(2)}\mathrm {d} n_{L}$

where μ $\mu$ denotes the chemical potential and the amount of substance passing the membrane. Since the influx of on side ⁽²⁾ is equal to the loss on side ⁽¹⁾ (conservation condition), it follows for the total change in free enthalpy:

$\ \mu ^{(2)}\mathrm {d} n_{L}=-\mu ^{(1)}\mathrm {d} n_{L}$ and thus $\mathrm {d} G=(\mu ^{(1)}-\mu ^{(2)})\mathrm {d} n_{L}$

As long as equilibrium has not yet been reached ( $\mathrm {d} G\leq 0$ ), the following holds for the chemical potentials:

$\mu ^{(1)}>\mu ^{(2)}$

and at equilibrium ( $\mathrm {d} G=0$ ):

$\mu ^{(1)}=\mu ^{(2)}$ .

If more than one type of substance participates in the osmotic process, the above relations must be extended by the chemical potentials of the additional components (see also section The osmotic potential of non-ideal solutions).

The condition for osmotic equilibrium is that the chemical potentials of the substances passed by the membrane (usually the solvent) are the same in both phases. As long as there is still a potential difference, particles of the respective component will move towards the lower potential. On the other hand, by increasing the chemical potential, for example by applying pressure or increasing the temperature on one side of the membrane, the direction of movement can be reversed. Osmosis through a membrane, unlike diffusion in a single-phase system, is a reversible process.

Solution effect as direct cause

The solution effect reduces the chemical potential of the solvent in the solution compared to the pure substance, combined with a lowering of the saturation vapour pressure in the case of liquids or the partial pressure in the case of gases. Thus the solution effect is a direct cause of osmosis.

In contrast, a concentration gradient of the dissolved substances has an indirect effect, since osmosis only occurs if the concentration differences lead to a difference in the chemical potential of the solvent in both solutions. If different substances are dissolved on both sides of the membrane in the same number of particles, the chemical potential of the solvent is the same and thus osmosis does not occur. This is the basis of the effect of osmolytes, with which cells can protect themselves against osmotic pressure.

Molecular kinetic observation

An approach to the explanation of osmosis by means of statistical mechanics was provided by Albert Einstein in 1905 in his work Über die von der molekularkinetischen Theorie der Wärme gefordertte Bewegung von in ruhenden Lösungen suspendierten Teilchen. In it, he describes that suspended particles differ from "redeemed" particles only in size, and that both therefore give rise to osmotic pressure according to the molecular theory of heat. According to Einstein, suspended particles are acted upon by a force that is in dynamic equilibrium with the osmotic pressure forces; the motion can be conceived as a superposition of two processes: A motion of suspended particles due to a force acting on each individual particle, and "a diffusion process as a result of the disordered molecular motion of heat."

Osmosis and mixture entropy

Osmosis - as diffusion of the solvent through a membrane into a solution - is a spontaneous mixing process. In general, a mixture of two liquids A and B has a higher entropy than the two separate substances, because in the common and thus larger volume there are more positions available at which each particle A or B can reside. Thus there is also a greater number of possible arrangements (microstates) for each of the two components than in the partial volumes of the separate substances, so that this long-range macrostate is the most probable. It is self-established by the thermal motion of the molecules. The measure of probability is entropy and therefore it has its maximum at this distribution. The solvent, in many practically important cases water, which diffuses through the selectively permeable membrane, mixes with the dissolved molecules. The entropy of the total system increases by this mixing entropy (however, there is no mixing entropy water/water Gibbs' paradox). In the calculation example, with 0.001 mol of solute and 0.1 liter of water diffusing through the membrane, one obtains a mixing entropy of ≈ 0.08 J K-1. One arrives at this result in two ways. One is via the mass fractions and the mean molar entropy of mixing or via the statistical weight of the state of mixing:

Thermodynamic

Molar quantities and molar quantity fractions :


(1) dissolved substance	0.001 mol	1,80653·10−4
(2) Water	5.53446 mol	0,999819

Mean molar mixture entropy: ${\overline {\Delta S_{\mathrm {mix} }}}=-R\cdot \left[x_{1}\cdot \ln(x_{1})+x_{2}\cdot \ln(x_{2})\right]=0{,}0144477\;\mathrm {J\,K} ^{-1}\,\mathrm {mol} ^{-1}$

This gives, for 5.53546 moles (i.e., the total molar amount): Δ $\Delta S_{\mathrm {mix} }=0{,}07997\;\mathrm {J\,K} ^{-1}$

Statistical

( means the number of molecules).

$\Delta S=k_{\mathrm {B} }\cdot \ln W\quad {\text{mit}}\quad W={\frac {(N_{1}+N_{2})!}{N_{1}!\cdot N_{2}!}}\quad {\text{also}}\quad W={\frac {(5{,}53546\cdot 6{,}02205\cdot 10^{23})!}{(0{,}001\cdot 6{,}02205\cdot 10^{23})!\cdot (5{,}53446\cdot 6{,}02205\cdot 10^{23})!}}$

Using the approximation $\ln(N!)\approx N\cdot \ln N$ , we obtain for the mixture entropy: Δ $\Delta S=0{,}07997\;\mathrm {J\,K} ^{-1}$

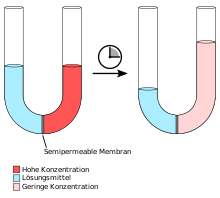
Osmosis: on the left a U-tube with differently concentrated solutions immediately after filling, on the right the same U-tube at a later time. Equilibrium is reached when the hydrostatic pressure of the liquid column on the right is equal to the osmotic pressure of the solution.

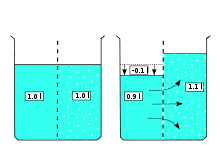
On the left of the membrane the solvent, on the right the solution. The inflow of solvent into the solution (right picture) increases the number of spatial arrangement possibilities, for the solvent as well as for the dissolved molecules. The reverse process of spontaneous segregation is extremely unlikely, but can be forced by applying pressure (reverse osmosis).

Osmotic pressure

Analogy to gas pressure

If a vessel filled with sugar solution (A) is placed in pure water (B) and its wall is impermeable only to the dissolved sugar molecules, the inflow of water will increase the pressure in the interior. The osmotic pressure thus produced will counteract the inflow of water; the movement of water will cease when equilibrium is reached (Fig. 1). The same pressure distribution as in Fig. 1 can be achieved without water inflow if (e.g. via a piston) an equal pressure acts on the liquid (A). (Fig. 2). Increasing or decreasing the piston pressure changes the concentration of the solution (A), as water then flows out or in through the vessel walls accordingly. This principle is used in reverse osmosis (also called anti-osmosis in older writings); a solution is further concentrated under pressure to remove the substances dissolved in it.

This fundamental analogy between osmotic and gas pressure was first described by the Dutch chemist van 't Hoff in 1887. He considered the cause of the osmotic pressure to be the collisions of the dissolved particles with the membrane wall (which is impermeable to them) (solute bombardment theory). The influence of the water molecules, on the other hand, was the same on both sides of the membrane and would therefore cancel each other out. This interpretation is contradicted by the fact that no deflection of the membrane is observed if the hydrostatic pressure is the same on both sides.

Application of the gas laws

In dilute liquid solutions the same laws apply as for ideal gases (Boyle-Mariotte law, Gay-Lussac law, Avogadro law). The osmotic pressure

is proportional to the molar concentration of the solute
is proportional to the absolute temperature
of solutions depends only on the number of particles of the solute (molar concentration) (→ colligative property).
of a solution of 1 mol in 22.4 l solvent is 101.325 kPa (standard pressure) at 273.15 K (0 °C).

These statements are summarized by van 't Hoff's law "the osmotic pressure is as great as the pressure of a gas of equal particle density and temperature ":

$\Pi ={\frac {n}{V}}\cdot i\cdot R\cdot T=c\cdot i\cdot R\cdot T$

Here is

$\Pi$ the osmotic pressure
c = n/V is the mass concentration (molar concentration) of the solution
i = Van-'t-Hoff factor (number of particles dissociating in water per molecule (e.g. for glucose; for NaCl))
is the universal gas constant
is the absolute temperature in K.

In this form, the law applies only to dilute solutions (< 0.1 mol/l), just as the ideal gas laws apply only at low pressures (the interaction of the particles with each other is neglected).

Osmotic pressure and vapour pressure

The vapour pressure of a solution is always lower than that of the pure solvent (dissolution or dilution effect). Adding a substance to lowers its chemical potential.

$\Delta \mu _{L}=RT\ln \left({\frac {P_{L}}{P_{\dot {L}}}}\right)$ .

Here is $P_{L}$ the vapor pressure of the pure solvent and $P_{\dot {L}}$ the solution. The osmotic pressure acts in the opposite way and leads to an increase of μ $\mu _{L}$

$\Delta \mu _{L}=\int _{0}^{\Pi }V_{L}^{m}\mathrm {d} P$

For liquids, the partial molar volume $V_{L}^{m}$ can be considered to be independent of pressure. Under this condition, from both above terms, the equation:

$V_{L}^{m}\Pi =RT\ln \left({\frac {P_{\dot {L}}}{P_{L}}}\right)$

can be derived. It states that the osmotic pressure is equal to the external pressure that would increase the vapor pressure of a solution to the vapor pressure of the pure solvent . The driving force of osmosis is the decrease in vapor pressure of the solvent caused by the solution effect. An osmotic cell is in equilibrium when the osmotic pressure is balanced by an equal opposing force.

Saline solutions (electrolytes)

The osmotic pressure of a salt solution is always higher than it corresponds to van 't Hoff's law in the form Π = c⋅R⋅T, and is often twice or three times as high. This effect is due to the fact that salts break down into negatively and positively charged ions during the dissolution process (→ dissociation) and, when dissolved, have a higher number of particles than corresponds to the amount of substance in the solid state. For completely dissolved salts (strong electrolytes), this is an integer multiple of the original amount of substance. By extending the equation by a factor:

$\Pi =i\cdot c\cdot R\cdot T$

this effect can be taken into account. Here the Van-'t-Hoff factor, a dimensionless number. For sodium chloride (NaCl), potassium chloride (KCl) and other binary electrolytes, i=2 ; for 1,2-valent electrolytes such as sodium sulfate (Na2SO4), i=3 .

For salts that do not completely decompose in solution (weak electrolytes), the Van 't Hoff factor can be $\alpha$ calculated from the degree of dissociation α

$i = 1 - \alpha + \nu \alpha$

where ν is $\nu$ the number of ions per salt molecule. Therefore, when specifying the concentration of ions, it can be useful to specify them in the units osmol-l-1 (osmolarity) or osmol-kg-1(osmolality), since dissociation is already taken into account here.

The osmotic potential of non-ideal solutions

The van 't Hoff law does not apply to solutions where the interaction of the molecules can no longer be neglected. Here, the chemical potential from the Gibbs fundamental equation must be used. In thermodynamic equilibrium, the free enthalpy (Gibbs energy) of an osmotic cell is minimal:

$\mathrm {d} G=V\cdot \mathrm {d} p-S\cdot \mathrm {d} T+\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} n_{i}=0$

At constant temperature, the equation simplifies to:

$0=V\cdot \mathrm {d} p+\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} n_{i}$

At constant ambient pressure, the following follows for the change in osmotic pressure:

$\mathrm {d} \Pi =-\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} c_{i}$ .

The osmotic pressure $\Pi$ is thus obtained with the molar densities $c_{i}$ from the change of all chemical potentials μ $\mu$ . In this equation, mixing effects of the substances involved are taken into account. However, usually the mixing effects of the solutes among themselves and the concentration of the solvent are neglected:

$\Pi =-RT\cdot \sum _{i=1}^{N}\Delta \left(c_{i}\cdot \ln a_{i}\right)$ .

Another approximation would be to neglect the mixing effect of the solute with the solvent. Here, the activity $a_{i}$ these substances is assumed to be one, resulting as a rough approximation:

$\Pi \approx -RT\cdot \sum _{i=1}^{N}\Delta c_{i}$ .

This approximate calculation can be used for dilute solutions, but leads to errors of more than 50 % for higher concentrations, especially since the solution effect is not taken into account here.

The negative value of the osmotic pressure is called the osmotic potential ψ . $\psi _{o}$

The osmotic coefficient and the ionic strength

There are various definitions of the osmotic coefficient.

The osmotic coefficient $f_{o}$ is defined, for example, as the quotient of the real measured osmotic pressure and the theoretically expected (calculated) osmotic pressure (at this concentration) of a salt solution or non-ionic solution (of molecular substances):

$f_{o}={\frac {\Pi _{\text{gemessen}}}{\Pi _{\text{berechnet}}}}$

Real dilute solutions would therefore always have a value less than or equal to one.

Empirically, the following correlation could be shown:

$f_{o,(c,z,I)}={1-K\cdot {\sqrt {I}}}$

is here a constant, the ionic strength. The Debye-Hückel theory led to the following theoretical equation for dilute electrolyte solutions:

$f_{o,(c,z,I)}={1-(2{,}303/3)\cdot A\cdot z_{+}\cdot z_{-}{\sqrt {I}}}$

A is a constant according to the Debye-Hückel theory. The ionic valences (charge numbers) z are to be inserted as amounts. This equation confirmed the empirically found first equation.

This osmotic coefficient is used, among other things, in electrochemistry. The coefficient says something about the deviation/approximation from/to the ideal state (ideal dilution at c=0 mol/liter or more precisely ionic strength I=0 mol/liter) of a solution. Ideally diluted solutions have an osmotic coefficient of the value one - according to this definition. At high concentrations (more precisely: ionic strengths) the value tends towards zero. Therefore, analogies exist to the degree of dissociation and the conductivity coefficient of electrolytic conductivity, because these values also run from (theoretically) zero (high concentration c or ionic strength I) to one (ideal dilution, c=0, I=0).

The ionic strength I, which was defined by Gilbert N. Lewis and Merle Randall in 1921, is also supposed to be a measure of the deviation of an electrolyte solution from the ideal state (obviously the comparison with the arithmetic mean of the molar concentrations is meant). For binary electrolytes (one cation and one anion), the ionic strength I is to be regarded as the arithmetic mean of the concentrations weighted quadratically according to the ionic valences (charge numbers).

Osmometry - measurement of the osmotic pressure

The osmotic pressure of a solution is determined using membrane osmometers similar to Pfeffer's cell. The pressure can be measured either statically, after equilibrium has been established, or dynamically, by applying an external pressure to the riser tube manometer which just interrupts the osmotic flow.

A 1 molar solution of cane sugar (molar mass 342.30 g-mol-1) in water already causes an osmotic pressure of 2.70 MPa (27 bar) at room temperature. For considerably higher pressures (several 100 bar), measurement principles such as the change in the refractive index of water or the piezoelectric effect can be used.

By measuring the osmotic pressure or potential, it is possible to determine the average molecular mass of macromolecules; this procedure is known as osmometry. Since there is a direct relationship between the osmotic pressure and the other colligative properties of a solution, these being boiling point increase and freezing point decrease, the osmotic pressure can be determined indirectly as an osmotic value by measuring them.

While the direct measurement of osmotic pressure requires the presence of two phases and a specifically permeable membrane, the indirect methods of osmometry only require the solution to be measured. They are therefore particularly suitable for characterizing different solutions with regard to their osmotic properties. Osmolarity and osmolality indicate the concentration of dissolved particles in relation to the volume or amount of substance. Isoosmotic are solutions whose osmotic value is the same. Since the osmotic value does not contain any information about the components in the solutions to be compared, isoosmotic cannot be equated with isotonic.

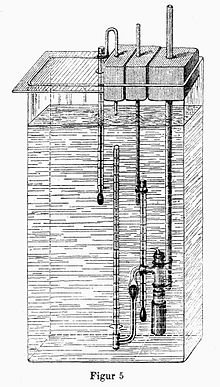
Pfeffer cell - prototype of the membrane osmometer

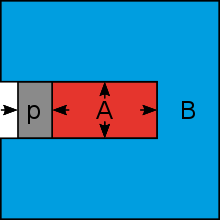
Fig. 2 Equalization of the osmotic pressure by means of a piston

Fig. 1 Osmotic pressure at equilibrium

Questions and Answers

Q: What is osmosis?

A: Osmosis is the movement of solvent (liquid) molecules through a membrane, from one solution to another, without an outside force. The solvent will move to the side with a higher concentration of solutes and lower concentration of solvent.

Q: How does osmosis work?

A: Osmosis works because the membrane is selectively permeable, allowing the solvent to pass through but not the solute. The solvent molecules move randomly and so concentrations on both sides become more equal. Osmotic pressure can be applied so that there is no net movement of solvent across the membrane.

Q: What factors affect permeability in biological membranes?

A: Permeability in biological membranes depends on solubility, charge or chemistry as well as solute size.

Q: How do water molecules travel through biological membranes?

A: Water molecules travel through biological membranes by diffusing across the phospholipid bilayer.

Q: What role does osmosis play in living systems?

A: In living systems, osmosis provides a way for water to get into and out of cells and it helps maintain turgor pressure within cells by creating an equilibrium between cell interior and its environment.

Q: How does molar concentration affect osmotic pressure?

A: Osmotic pressure depends on molar concentration of the solute; higher concentrations require more external pressure for there to be no net movement of solvent across the membrane.