Numerical integration

In numerical mathematics, numerical integration (traditionally also called numerical quadrature) refers to the approximate computation of integrals.

Often integrals cannot be solved in a closed way, because the integrand cannot be given as a primitive function or it is only given by discrete values, e.g. measurements. Then one tries to determine approximate values.

For this purpose, the integral of a function over the interval [a,b] is represented as the sum of the value of Q(f) an approximation formula (also called a quadrature formula) and an error value E(f) :

$\int _{x_{u}}^{x_{o}}f(x)\,dx=Q(f)+E(f)\,.$

The idea of numerical computation of integrals borrows directly from the definition of the Riemann integral.

Numerical integration seeks the simplest possible approximation for the surface $S=\int _{x_{u}}^{x_{o}}f(x)\,dx$

Quadrature Procedure

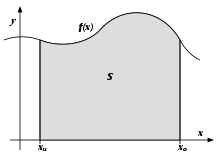
Graphical methods

In graphical methods, the graph of the integrand is plotted in a coordinate system with linear axes and the area between the graph and the abscissa is determined.

Counting method

A particularly simple procedure is to plot the graph on graph paper and then determine the number of "square millimetre boxes" (area elements) covered by the area S. In this case, only half of the area elements through which the graph passes are counted. Here, area elements through which the graph passes are only counted by half. The approximation then results with the number of square millimeters and the scale parts Δ $\Delta x$ and Δ $\Delta y$ to:

$\int _{a}^{b}f(x)\,dx\approx Nmm^{2}\cdot {\tfrac {\Delta x}{mm}}\cdot {\tfrac {\Delta y}{mm}}$

Measurement

Another graphical method is the measurement of the area by means of a planimeter.

quadrature formula calculation

In general, a quadrature formula consists of a weighted sum of function values

$Q(f)=(x_{o}-x_{u})\sum _{i=0}^{n}w_{i}f(x_{i}).$

The places $x_0,\ldots, x_n$ called supporting places and the numbers $w_0,\ldots,w_n$ weights. The weights here depend on the distances of a grid point to the neighboring grid points. There are different approaches how to choose grid points and weights in a way that the quadrature error as small as possible. E(f)

A quadrature formula has the degree of precision (or exactness) if it integrates all polynomial functions up to the maximum degree exactly, and is the largest possible natural number with this property.

Like the integral, quadrature formulas are linear operators.

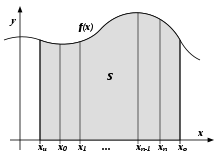
interpolation points

Interpolatory quadrature formula

An important class of quadrature formulas arises from the idea of approximating the function f(x) by an interpolation polynomial p_n(x) of degree and then integrating it. The weights are then obtained as the integrals of the Lagrange polynomials to the given support points. By construction, these quadrature formulas have at least degree of accuracy . The quadrature formula is therefore

$\int _{a}^{b}f(x)\,dx\approx \int _{a}^{b}p_{n}(x)\,dx=(b-a)\sum _{i=0}^{n}w_{i}f(x_{i})$

with the weights

$w_{i}={\frac {1}{b-a}}\int _{a}^{b}L_{in}(x)\,dx$

and the Lagrange polynomials

$L_{in}(x)={\frac {(x-x_{0})\dotsm (x-x_{i-1})(x-x_{i+1})\cdots (x-x_{n})}{(x_{i}-x_{0})\dotsm (x_{i}-x_{i-1})(x_{i}-x_{i+1})\dotsm (x_{i}-x_{n})}}.$

If the integration limits are support points, one speaks of closed quadrature formulas, otherwise of open ones. If the support points are chosen equidistantly, the Newton-Cotes formulas result among others. Among the closed Newton-Cotes formulas are the chordal trapezoid rule and Simpson's rule, among the open ones is the tangent trapezoid rule. The Newton-Cotes formulas for even even have the degree of precision n+1 . The open quadrature formulas also include the Gauss quadrature formulas.

Error estimation

Let [c,d] denote the smallest interval [a,b] containing the interpolation points $x_{i}$ and the interval Furthermore, let (n+1) -times continuously differentiable on [c,d] . According to the interpolation quality of the interpolation polynomial, there exists a ξ $\xi(x) \in [c,d]$ , such that holds:

$f(x) - p_n(x) = \frac{f^{(n+1)}(\xi(x))}{(n+1)!} \prod_{i=0}^n (x-x_i).$

By integration, the error formula for numerical quadrature is obtained

$E(f)=\int _{a}^{b}f(x)\,dx-\int _{a}^{b}p_{n}(x)\,dx={\frac {1}{(n+1)!}}\int _{a}^{b}f^{(n+1)}(\xi (x))\prod _{i=0}^{n}(x-x_{i})\,dx$ .

If $f^{(n+1)}(x)=0$ for all $x \in [c,d]$ , the quadrature error is 0. Since this is the case for all polynomials up to degree , the degree of accuracy of these quadrature formulas is at least .

From this error formula follows the error estimate

$|E(f)|\leq {\frac {1}{(n+1)!}}\ \max _{c\leq x\leq d}{\left|f^{(n+1)}(x)\right|}\int _{a}^{b}\left|\prod _{i=0}^{n}(x-x_{i})\right|\,dx$ .

If the function $\prod_{i=0}^n (x-x_i)$ in the interval not change [a,b] its sign, i.e., if no support point (a,b) lies in the interval , one can derive the following representation for the remainder element using the mean value theorem of integral calculus:

$E(f)={\frac {f^{(n+1)}(\zeta )}{(n+1)!}}\int _{a}^{b}\prod _{i=0}^{n}(x-x_{i})\,dx$ .

With an intermediate $\zeta \in [c,d]$ .

Similar formulas for the quadrature error are also obtained for special distributions of the grid points in the interval [a,b] for example for the Newton-Cotes formulas or the Gauss quadrature formulas.

If the function is only continuous, the above statements do not hold, the error can become very large.