Number
![]()
This article is about the mathematical term number. For other meanings, see Number (disambiguation).
Numbers are abstract mathematical objects or objects of thought that developed historically from ideas of size and number. Through a measurement, an aspect of an observation understood as a quantity is associated with a number, for example in a count. They therefore play a central role in the empirical sciences.
In mathematics, which formally studies numbers and their structure, the term includes diverse concepts. These developed as generalizations of existing intuitive number concepts, so that they are also called numbers, although they have little relation to the concepts originally associated with measurements. Some of these concepts are fundamental to mathematics and are used in almost all subfields.
The concept of natural numbers, which can be used for counting and have fundamental meaning, goes back to prehistory. From about 2000 BC, Egyptians and Babylonians calculated with fractions (rational numbers). In India, an understanding of zero and negative numbers developed in the 7th century AD. Irrational numbers such as 

The idea of imaginary numbers, through which the real numbers were later extended to the important complex numbers, goes back to the European Renaissance. The concept of the real number was not adequately clarified until the 19th century. At the end of the 19th century, it was possible for the first time to give infinite quantities a precise meaning as numbers. The natural numbers were also defined axiomatically for the first time. With the first satisfactory foundations of mathematics created at the beginning of the 20th century, the most important number concepts were also given a completely formal definition and meaning corresponding to the current state of affairs.
To be distinguished from the concept of number are numerals (special number signs; characters used to represent certain numbers), number scripts (ways of writing numbers, e.g. with the aid of numerals, using certain rules), number words (numerals, words used to designate certain numbers) and numbers (identifiers, which can themselves be numbers, or else - as a rule - strings of characters containing numerals).
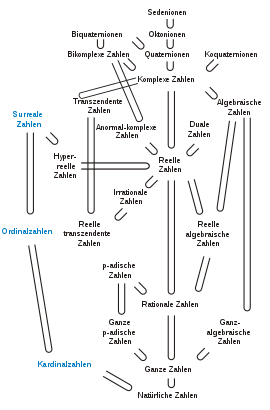
Overview of some common number ranges. 


Etymology
The German word Zahl (number) probably goes back to the Ur-Germanic word *talō (calculation, number, speech), which is probably the root of the Old High German words zala (order, orderly presentation, report, enumeration) and zalōn (report, reckon, count, calculate, pay). In Middle High German, zala became zale or zal, to which the modern word Zahl goes back.
The Ur-Germanic word probably finds its origin in a Ur-Indo-European etymon *del- (to aim, to calculate, to readjust). A connection with the Urindogermanic *del- (to split) is also possible; the original meaning would then possibly be "notched marker".
Definition of numbers
The term number is not defined mathematically, but is a common language generic term for various mathematical concepts. Therefore, in the mathematical sense, there is no set of all numbers or the like. When mathematics deals with numbers, it always talks about certain well-defined number ranges, i.e. only about certain objects of our thinking with fixed properties, all of which are casually referred to as numbers. Since the end of the 19th century, numbers have been defined in mathematics purely by means of logic, independently of ideas of space and time. The foundations for this were laid by Richard Dedekind and Giuseppe Peano with their axiomatization of the natural numbers (see Peano axioms). Dedekind writes about this new approach:
"What is provable should not be believed in science without proof. As plausible as this demand may seem, it is still, as I believe, by no means to be regarded as fulfilled even in the justification of the simplest science, namely that part of logic which deals with the doctrine of numbers, even according to the most recent representations. [...] Numbers are free creations of the human mind; they serve as a means of comprehending the diversity of things more easily and more sharply. Through the purely logical structure of the science of numbers and through the constant realm of numbers obtained in it, we are only put in a position to examine our ideas of space and time precisely by relating them to this realm of numbers created in our spirit."
- Richard Dedekind: What are and what are the numbers for? Preface to the first edition.
Axiomatic definitions are to be distinguished from set-theoretic definitions of numbers: In the former case, the existence of certain objects with links defined on them with certain properties is postulated in the form of axioms, as for instance also in the early axiomatizations of the natural and the real numbers by Peano and Dedekind. Following the development of set theory by Georg Cantor, one proceeded to try to restrict oneself to set-theoretic axioms, as is common in mathematics today, for example, with the Zermelo-Fraenkel set theory (ZFC). The existence of certain sets of numbers and relations over them with certain properties is then inferred from these axioms. Sometimes a number range is defined as a certain class. Axiomatic set theory attempts to be a single, unified formal foundation for all of mathematics. Within it, number domains can be dealt with in rich ways. As a rule, it is formulated in first-level predicate logic, which determines the structure of mathematical propositions as well as the possibilities of inference from axioms.
An elementary example of a set-theoretic definition of a set of numbers is the definition of the natural numbers introduced by John von Neumann as the smallest inductive set, whose existence is postulated by the infinity axiom in the context of Zermelo-Fraenkel set theory.
As set-theoretic concepts, ordinal and cardinal numbers are usually defined in set-theoretic terms, as is the generalization of surreal numbers.
The Peano axioms, for example, and the definition of the real numbers going back to Dedekind are, in contrast to ZFC, based on second-level predicate logic. While first-stage predicate logic provides a clear, generally accepted answer as to how valid inferences are to be made, whereby these can be systematically computed, attempts to clarify this for second-stage predicate logic usually lead to the need to introduce a complex metatheory, which in turn introduces set-theoretic notions meta-linguistically, and on the details of which depend the possibilities of inference in second-stage predicate logic that are subsequently opened up. ZFC is a candidate for such a theory. These limitations make second-level predicate logic seem unsuitable to be used at a fundamental level in part of the philosophy of mathematics. First-level predicate logic, on the other hand, is insufficient to formulate and (when considering these in a set-theoretic metatheory, say, due to Löwenheim-Skolem's theorem, countability) ensure certain important intuitive properties of the natural numbers.
Questions and Answers
Q: What is a number?
A: A number is a concept from mathematics used to count or measure.
Q: What are numerals?
A: Numerals are symbols that represent numbers.
Q: Where are numerals used?
A: Numerals are commonly used for labeling, ordering, and putting unique identifiers.
Q: What is the purpose of cardinal numbers?
A: Cardinal numbers are used to measure how many items are in a set.
Q: What do ordinal numbers do?
A: Ordinal numbers specify a certain element in a set or sequence (first, second, third).
Q: How else can we use numbers?
A: Numbers can be used for counting and measuring things, as well as studying how the world works through mathematics and engineering.
Search within the encyclopedia