Nth root

In mathematics, root extraction or root extraction is the determination of the unknown in the power

$a=x^{n}\,$

Here, is a natural number (usually greater than 1) and is an element from a body (often a non-negative real number). The result of root extraction is called a root or radical (from Latin radix "root"). Radixing is an inversion of exponentiation. In the case n=2 one speaks of square roots, in the case n=3 of cube roots. Roots are notated using the root sign, in the example $x:={\sqrt[{n}]{a}}$ the root or radical.

Graphical representation of the square root function $y={\sqrt {x}}$

In double logarithmic order the -th roots become straight lines.

Definition, Speech and Spelling

Let $n\geq 1$ be a natural number. If is a nonnegative real number, then the equation has

$x^{n}=a$

exactly one non-negative real solution. This is called the -th root of . One writes for it:

$x={\sqrt[{n\,}]{a}}$

Here one designates

${\sqrt[{n\,}]{a}}$ as root, radical or radix,
${\sqrt {\;\;}}$ as the root character,
as the root exponent,
as a radicand.

In the special case n=1 get a ${\sqrt[{1\,}]{a}}=a$ .

square and cube root

Usually the second root is called the square root or just the root and the root exponent is omitted:

${\sqrt {a}}={\sqrt[{2}]{a}}$

The root with the root exponent 3 (third root) is also called the cube root.

Example:

${\sqrt[{3}]{8}}=2$

(Say: The third root of 8 is 2 or The cube root of 8 is 2)

Mathematical basics

The following description of radixing as a right-unique root function refers to the ordered body $\mathbb{R}$ of the real numbers, that is, in a sense, to school mathematics. A more general notion of roots, encompassing the one described here, is treated in the article Adjunction (Algebra).

Connection with powers

Rooting with the root exponent and exponentiating with the exponent cancel each other. According to the above definition of the root, for all real numbers $a\geq 0$ and for all natural numbers $n\geq 1$ :

$\left({\sqrt[{n}]{a}}\right)^{n}=a$

The root exponent same effect as the exponent ${\tfrac {1}{n}}$ . Indeed, according to the rules of calculation for powers:

$\left(a^{\frac {1}{n}}\right)^{n}=a^{\frac {n}{n}}=a^{1}=a$

Therefore, radixing with the root exponent n can also be interpreted as exponentiating with the exponent 1/n:

${\sqrt[{n}]{a}}=a^{\frac {1}{n}}$

Uniqueness of roots from positive numbers

Although the problem mentioned at the beginning has two solutions with different signs for even root exponents and positive radicands, the notation with the root sign ${\sqrt[{}]{}}$ basically stands for the positive solution. For example, the equation $x^{2}=4$ has the two solutions $x=+2$ and x=-2 . However, the term ${\sqrt[{2}]{4}}$ has the value +2 and not the value -2. In general, therefore, the following applies to even-numbered root exponents

${\sqrt[{2n}]{x^{2n}}}=|x|\,.$

Roots from negative numbers

The treatment of roots from negative numbers is not uniform. It is valid for example

$(-2)^{3}=-8\,,$

and is the only real number whose third power is . In general, odd powers of negative numbers result in negative numbers again.

Regarding odd roots from negative numbers, the following positions are taken:

Roots of negative numbers are generally undefined. For example, ${\sqrt[{3}]{-8}}$ is thus undefined. The solution to the equation $x^{3}=-8$ is written as $x=-{\sqrt[{3}]{8}}$ .
Roots of negative numbers are defined when the root exponent is an odd number (3, 5, 7, ...). For odd numbers holds in general

${\sqrt[{2n+1}]{-a}}=-{\sqrt[{2n+1}]{a}}$ .

This determination is inconsistent with some properties of roots that apply to positive radicands. For example

$-2={\sqrt[{3}]{-8}}\neq {\sqrt[{6}]{(-8)^{2}}}={\sqrt[{6}]{64}}=+2.$

Also, this definition does not work with the equation ${\sqrt[{k}]{a}}=a^{\frac {1}{k}}=\exp \left({\tfrac {1}{k}}\ln(a)\right)$ , since the (natural) logarithm of negative numbers is not defined ( so must not be negative).

Roots to even exponents of negative numbers cannot be real numbers, because even powers of real numbers are never negative. There is no real number , so $x^{2}=-1$ , so you cannot $x={\sqrt[{2}]{-1}}$ find a root the real numbers. The need for roots of negative numbers led to the introduction of the complex numbers; however, there are certain difficulties with the concept of roots in the domain of the complex numbers with the unique labeling of one of the roots, see below.

Irrational roots from integers

If is a nonnegative integer and is a positive integer, then ${\sqrt[ {k}]{n}}$ either an integer or an irrational number. This is proved by applying the uniqueness of the prime factorization:

If $n\leqq 1$ , then ${\sqrt[{k}]{n}}=n$ , that is, an integer. Otherwise, there is a prime factorization $n=p_{1}^{e_{1}}\dotsm p_{r}^{e_{r}}$ with pairwise distinct primes $p_{1},\dotsc ,p_{r}$ and positive integer exponents $e_{1},\dotsc ,e_{r}$ . If all $e_{j}$ for are divisible $1\leqq j\leqq r$ by , so ${\sqrt[{k}]{n}}=p_{1}^{e_{1}/k}\dotsm p_{r}^{e_{r}/k}$ , i.e., an integer.

Now it remains to show: If there is at least one with $1\leqq j\leqq r$ such that $e_{j}$ is not divisible by , then ${\sqrt[ {k}]{n}}$ irrational. The proof of irrationality is indirect, that is, by refuting the opposite assumption as in the proof of the irrationality of the square root of 2 in Euclid, which is essentially the special case n=k=2 this proof.

Suppose ${\sqrt[ {k}]{n}}$ were rational. Then you could write the number as a fraction of two natural numbers and

${\sqrt[{k}]{n}}={\frac {a}{b}}$ .

By exponentiating the equation you get

$n={\frac {a^{k}}{b^{k}}}$

and from this follows

$nb^{k}=a^{k}$ .

The prime factor $p_{j}$ occurs in $a^{k}$ or $b^{k}$ times as often as in resp. in any case in a multiplicity divisible by , although of course the occurrence 0 times is also allowed. In it occurs presuppositionally in the multiplicity $e_{j}$ not divisible by . So on the left-hand side of this equation it does not occur in a manifold divisible by , but on the right-hand side it does, and we get a contradiction to the uniqueness of the prime factorization. Therefore, is ${\sqrt[ {k}]{n}}$ irrational.

The root laws

The calculation rules for roots follow from those for powers.

For positive numbers and and the following computational laws hold $n,m,k\in \mathbb {N}$ :

Product rule: ${\sqrt[{n}]{a}}\cdot {\sqrt[{n}]{b}}={\sqrt[{n}]{a\cdot b}}$
Quotient rule: ${\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}={\sqrt[{n}]{\frac {a}{b}}}$
"Nesting rule" or iteration rule: ${\sqrt[ {m}]{{\sqrt[ {n}]{a}}}}={\sqrt[ {m\cdot n}]{a}}$
Definition for fractional exponents: $a^{\frac {k}{n}}={\sqrt[{n}]{a^{k}}}=\left({\sqrt[{n}]{a}}\right)^{k}$
Definition for negative exponents: $a^{-{\frac {k}{n}}}={\frac {1}{a^{\frac {k}{n}}}}$
With the same radicand, ${\sqrt[{m}]{a}}\cdot {\sqrt[{n}]{a}}=a^{{\frac {1}{m}}+{\frac {1}{n}}}={\sqrt[{mn}]{a^{m+n}}}$

For negative numbers and these calculation laws may only be applied if and are odd numbers. For complex numbers, they are to be avoided altogether, or equality applies only if the adjoint values are chosen appropriately. In other words, if any roots (e.g., only principal values) are chosen on the left side in an example, there are suitable minor values for the right side that satisfy equality - left and right sides differ by one unit root.

Limit values

The following limits apply:

$\lim _{n\rightarrow \infty }{\sqrt[{n}]{a}}=1$ for
$\lim _{n\rightarrow \infty }{\sqrt[{n}]{n}}=1$

This follows from the inequality $n<\left(1+{\sqrt[{2}]{\tfrac {2}{n}}}\right)^{n}$ , which can be shown using the binomial theorem.

$\lim _{n\to \infty }{\sqrt[{n}]{n^{k}}}=1$ , where an arbitrary but fixed natural number.
$\lim _{n\rightarrow \infty }{\frac {\ln(n)}{n}}=0$ ,

as can be seen from the exponential representation of . ${\sqrt[{n}]{n}}$

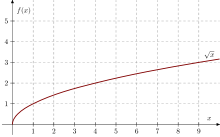
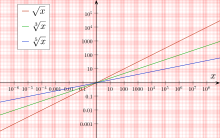
Root functions

Shape functions

$f\colon \mathbb {R} _{0}^{+}\to \mathbb {R} _{0}^{+},x\mapsto {\sqrt[{n}]{x}}$ or more generally $x\mapsto {\sqrt[{n}]{x^{m}}}$

are called root functions. They are power functions, it holds ${\sqrt[{n}]{x^{m}}}=x^{\frac {m}{n}}$ .

Questions and Answers

Q: What is an n-th root?

A: An n-th root of a number r is a number which, if multiplied by itself n times, produces the number r.

Q: How is an n-th root written?

A: An n-th root of a number r is written as r^(1/n).

Q: What are some examples of roots?

A: If the index (n) is 2, then the radical expression is a square root. If it is 3, it is a cube root. Other values of n are referred to using ordinal numbers such as fourth root and tenth root.

Q: What does the product property of a radical expression state?

A: The product property of a radical expression states that sqrt(ab) = sqrt(a) x sqrt(b).

Q: What does the quotient property of a radical expression state?

A: The quotient property of a radical expression states that sqrt(a/b) = (sqrt(a))/(sqrt(b)), where b != 0.

Q: What other terms can be used to refer to an n-th root?

A: An n-th root can also be referred to as a radical or radical expression.